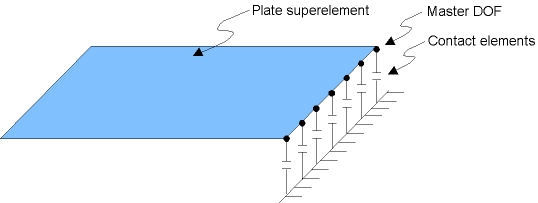
The generation pass is where you condense a group of "regular" finite elements into a single superelement. The condensation is done by identifying a set of master degrees of freedom, used mainly to define the interface between the superelement and other elements and to capture dynamic characteristics for dynamic analyses. Figure 2.2: Example of a Substructuring Application shows a plate-like structure that is to be analyzed with contact (interface) elements. Since the contact elements require an iterative solution, substructuring the plate portion can result in a significant savings in computer time. The master DOF required in this case are the degrees of freedom that connect the plate to the contact elements.
Generating a superelement involves two primary tasks:
In this step, you specify the jobname and analysis title and then use /PREP7 to define the element types, element real constants, material properties, and the model geometry. These tasks are common to most analyses and are described in the Basic Analysis Guide.
For the generation pass, consider the following:
Jobname -- The job name takes on special significance in a substructure analysis. By using jobnames effectively, you can eliminate much of the file-handling inherent in a three-pass analysis. For example, /FILNAME,GEN specifies the jobname GEN to all files created during the generation pass.
Element Types -- Most element types can be used to generate a substructure. In general, the only restriction is that elements within the superelement are assumed to be linear and cannot use Lagrange multipliers. If you include bilinear elements, they will be treated as linear elements (in their initial state).
Caution: Coupled-field elements used in a direct method coupled-field analysis with load vector coupling are not valid in a substructure analysis. Instead, use other elements in the same shape family. For more information, see the Coupled-Field Analysis Guide.
Also, elements with Lagrange multipliers cannot be used in substructuring. Such elements include:
Material Properties -- Define all necessary material properties. For example, if the mass matrix is to be generated, density (DENS) (or mass in some form) must be defined; if the specific heat matrix is to be generated, the specific heat (C) must be defined; and so on. Again, because a superelement is linear, any nonlinear material properties are ignored.
Model Generation -- In the generation pass, your primary concern is creating the superelement portion of the model. The nonsuperelement portion, if any, is defined later in the use pass. However, you should plan the modeling approach for both portions before you start building the model. In particular, decide on how you want to connect the superelement to the other elements. To ensure the connection, use the same node numbers at the interface. (Other methods requiring less effort on your part are discussed in the use pass section later in this chapter.)
Edge Outline -- Adjust the edge outline used to plot the superelement in the use pass (/EDGE). A smaller angle will produce more edges.
One approach is to develop the entire model, save it on a named database file, and select only the portion to be substructured for the generation pass. In the use pass then, you can RESUME from the named database file, unselect the portion that was substructured, and replace it with the superelement matrix. For more information, see Top-Down Substructuring.
The "solution" from a substructure generation pass consists of the superelement matrix (or matrices). As with any other analysis, you define the analysis type and options, apply loads, specify load step options, and initiate the solution. Details of how to do these tasks are explained below.
Enter the SOLUTION processor (/SOLU).
Define the analysis type and analysis options
Define the analysis type and relevant options using the ANTYPE
command. If the run is a restart, set STATUS = REST on
the ANTYPE command. A restart is applicable if you need to
generate additional superelement load vectors. The following files from the initial
run must be available for the restart: Jobname.esav,
Jobname.db, and Jobname.emat (if created
in the initial run).
Note: Restarting a substructure analysis is valid only if the backsubstitution method is chosen. You cannot restart a run if the full resolve option is selected using the SEOPT command.
Issue the SEOPT to specify the name of the superlement matrix
file (Sename) as well as other substructure analysis
options by defining various arguments described below (see the
SEOPT command definition for more details).
Matrices to be generated -- You can request
generation of just the reduced stiffness matrix (or conductivity matrix); stiffness
and mass matrices (or specific heat); or stiffness, mass, and damping matrices by
setting SEMATR on the SEOPT command.
The mass matrix is required if the use pass is a
structural dynamic analysis or if you need to apply inertia loads in the use pass.
For the thermal case, the specific heat matrix is required only if the use pass is a
transient thermal analysis. Similar considerations apply to other disciplines and to
the damping matrix.
Note: Verify that damping is present in the substructure model when using
SEMATR = 3 on the SEOPT command.
If not, a null reduced damping matrix is generated and stored in the associated
.sub file, which can increase the size of the file.
For first-order non-structural analysis types (thermal, electric, magnetic,
diffusion), whereas the matrix associated with the first-order degrees of
freedom (for instance, specific heat for thermal analysis) is the equivalent of
a damping matrix in structural analysis, the reduction of all matrices is
specified with SEMATR = 2 on the
SEOPT command. For coupled-field analyses, only the reduction
of the stiffness matrix (or the equivalent matrix) is possible.
Matrices to be printed -- You can request
listing both load vectors and superelement matrices or just the load vectors by
specifying SEPR on the SEOPT command.
If unspecified, the default is to not print any matrices.
Expansion Pass Method -- Select the expansion pass method you plan to use during
subsequent expansion passes with this superelement by specifying
EXPMETH on the SEOPT command. The
backsubstitution method (default) saves the factorized matrix files needed to
perform a backsubstitution of the master DOF solution during the expansion pass. The
factorized matrix files are named Sename.LNxx for the sparse
solver.
Factorized matrix files can become very large as the problem size increases, but
they are not needed and not saved if you set the full resolve
(EXPMETH = RESOLVE on SEOPT) expansion
pass method. This can be an effective way to save disk space usage as long as the
use pass does not include large-deflection effects.
During the expansion pass, the full resolve method reforms the elements used to create the superelement, reassembles the global stiffness matrix, and applies the master DOF solution as displacement boundary conditions internally. These displacement boundary conditions are deleted upon finishing the expansion pass solution.
Note: You cannot restart a substructure analysis with the full resolve expansion pass method chosen.
Mass matrix formulation -- Applicable only if you want the mass matrix to be generated. You can choose between the default formulation (which depends on the element type) and a lumped mass approximation. For most applications, the default formulation is recommended. However, for dynamic analyses involving "skinny" structures, such as slender beams or very thin shells, the lumped mass approximation has been shown to give better results. To specify a lumped mass approximation, issue the LUMPM command.
Equation Solver -- The SPARSE solver is the only solver available for the generation pass of the substructure analysis.
Modes to be used -- For superelements being used in a subsequent dynamic analysis (modal, harmonic, or transient), you may include mode shapes as extra degrees of freedom to obtain better accuracy (CMSOPT). See the chapter on Component Mode Synthesis for more information.
Define master degrees of freedom (M)
In a substructure, master degrees of freedom serve three purposes:
They serve as the interface between the superelement and other elements. Define master degrees of freedom at all nodes that connect to nonsuperelements, as shown in Figure 2.2: Example of a Substructuring Application. All degrees of freedom at these nodes should be defined as master degrees of freedom (
Lab= ALL on the M command). Master degrees of freedom must be defined even if you plan to have no elements in the model other than a superelement.If the superelement is to be used in a dynamic analysis, master degrees of freedom characterize the dynamic behavior of the structure if the component mode synthesis method (CMSOPT) is not used. See Modal Analysis in the Structural Analysis Guide for guidelines.
If constraints (D) or force loads (F) are to be applied in the use pass, master degrees of freedom must be defined at those locations with the M command.
If this superelement is to be transformed (SETRAN) later in the use pass or used in a large deflection analysis (NLGEOM,ON), then all nodes that have master degrees of freedom must have all six degrees of freedom (UX, UY, UZ, ROTX, ROTY, ROTZ) defined and active.
For large deflections, master degrees of freedom are typically defined at the joints of the flexible body and are at the nodes connected to a joint element (MPC184), another rigid or flexible body node, or ground. At least two master degrees of freedom must be defined for each substructure, as the average rotation of the superelement is computed from the average rotation of its master DOF. If only one node is a joint node, then another must be chosen at the free end. See the Multibody Analysis Guide for more details.
You can apply all types of loads in a substructure generation pass. Some types of loading involve certain considerations, as follows:
The program generates a load vector that includes the effect of all applied loads. One superelement load vector per load step is written to the superelement matrix file. This load vector represents the combination of the loads defined during the load step.
The maximum number of load vectors that can be generated and stored in the Sename.sub file defaults to 31. To change this limit, use
Lab= NUMSUBLV on the /CONFIG command.Nonzero degree of freedom constraints can be used in the generation pass and will become part of the load vector.
In the expansion pass, if the load step being expanded contains nonzero degree of freedom constraints, the database must have matching degree of freedom values. If it does not, the degree of freedom constraints must be specified (D) again in the expansion pass.
Application of constraints (D) or force loads (F) can be postponed until the use pass, but a master degree of freedom must be defined at those locations with the M command or corresponding GUI path.
If a mass matrix is generated, apply the degree of freedom constraints in the use pass at the master degree of freedom (defined in the generation pass) to ensure that all mass is accounted for in the substructure. For analyses with acceleration loadings, the load should be applied in the generation pass and used in the use pass for greater accuracy, rather than apply the acceleration load on the reduced mass matrix.
Similarly, application of angular accelerations can be postponed until the use pass, but only if a mass matrix is generated. A postponement is desirable if you plan to rotate the superelement in the use pass, because load vector directions are "frozen" and rotated with the superelement.
The Maxwell force flag (MXWF label on the SF family of commands) is normally used in a magnetic analysis to flag element surfaces on which the magnetic force distribution is to be calculated. The flag has no effect (and therefore should not be used) for a superelement in a magnetic analysis.
If you intend to create an imaginary force vector, generate it as a real load vector, then use it as an imaginary load vector in the use pass (SFE,,,,
KVAL= 2) and expansion pass (SEEXP,,,ImagKy= ON).When a load vector exists for a thermal superelement, it must be applied and have a scale factor of 1 (SFE,,,,,SELV,,1).
For large-rotation analyses, do not apply constraints to the model in this pass, as you will apply constraints for large rotation analyses in the use pass.
Table 2.1: Substructure Analysis Loads
| Load Name | Load Category | Commands[a] | |
|---|---|---|---|
| Solid Model Loads | Finite Element Loads | ||
| Displacement Temperature Mag. Potential ... | Constraints | DK, DKLIST, DKDELE, DL, DLLIST, DLDELE, DA, DALIST, DADELE, DTRAN | D, DSYM, DLIST, DDELE, DSCALE, DCUM |
| Force Heat Flow Rate Mag. Flux ... | Forces | FK, FKLIST, FKDELE, FTRAN | F, FLIST, FDELE, FSCALE, FCUM |
| Pressure Convection Maxwell Surface ... | Surface Loads | SFL, SFLLIST, SFLDELE, SFA, SFALIST, SFADELE, SFGRAD, SFTRAN | SF, SFLIST, SFDELE, SFE, SFELIST, SFEDELE, SFBEAM, SFGRAD, SFFUN, SFSCALE, SFCUM |
| Temperature Heat Generation Rate Current Density ... | Body Loads | BFK, BFKLIST, BFKDELE, BFL, BFLLIST, BFLDELE, BFA, BFALIST, BFADELE, BFV, BFVLIST, BFVDELE, BFTRAN | BF, BFLIST, BFDELE, BFE, BFELIST, BFEDELE, BFSCALE, BFCUM |
| Gravity, Linear and Angular Acceleration | Inertia Loads | ACEL, DOMEGA | |
[a] The menu path used to access each command in the GUI will vary depending on the engineering discipline of the analysis (structural, magnetic, etc.). For a list of menu paths, see the description of individual commands in the Command Reference.
Specify load step options
The only options valid for the substructure generation pass are dynamics options (damping), listed in the table below.
Table 2.2: Commands to Specify Damping Options (Applicable only if the damping matrix is to be generated.)
Start solution calculations (SOLVE).
Output from the solution consists of the superelement matrix file,
Sename.sub, where
Sename is the name assigned as an analysis option
(SEOPT) or the jobname (/FILNAME). The
superelement matrix file includes a load vector calculated based on the applied
loads. (The load vector will be zero if no loads are defined.)
Save a backup copy of the database on a named file (SAVE).
Saving a backup copy of the database is required because you need to work with the same database in the expansion pass. To support running the expansion pass in distributed-memory parallel mode, the database must be saved after the SOLVE command.
Repeat for additional load steps (that is, to generate additional superelement load vectors).
The superelement load vectors are numbered sequentially (starting from 1) and appended to the superelement matrix file. See Loading in the Basic Analysis Guide for other methods for multiple load steps.
Leave the SOLUTION processor (FINISH).