Contact element CONTA177 follows the contact pair concept used by the surface-to-surface elements (CONTA172 and CONTA174). You must pair CONTA177 with 3D target surface segments (TARGE170) to model 3D beam-to-surface or 3D shell edge-to-surface contact. See Identifying Contact Pairs for more information. CONTA177 uses most of the same element KEYOPTs and real constants as the surface-to-surface contact elements. Any differences are described in the next section.
The basic steps for performing a 3D line-to-surface contact analysis are the same as those used for a typical surface-to-surface analysis. See Steps in a Contact Analysis for details.
When the underlying elements are beams or edges of shell elements you can use the ESURF command to create CONTA177 elements. This procedure is similar to that used for the surface-to-surface contact elements.
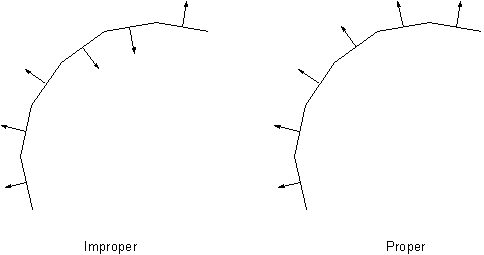
When using line-to-surface contact elements to form the contact surface, the nodes must be entered in a sequence that defines a continuous line, as shown in the figure below.
The line can be made up of linear or parabolic segments, depending on whether the attached beam or shell edge is made up of first order or second order elements. If the nodal ordering of the underlying beam elements is not consistent, you must either change the node ordering by reversing the node number order of the selected elements (ESURF,,REVERSE command) or make a consistent element ordering (ENORM command).
You can list the CONTA177 results using the PRESOL,CONT or PRETAB commands. Since CONTA177 is a 3D line element, you can also use the PLLS command to display element table items.
The following table shows the various contact (CONT) result items available via the PLNSOL and PLESOL commands.
| CONT | STAT | Contact status[2]:
| ||||
| " | PENE | Contact penetration | ||||
| " | PRES[2] | Contact pressure | ||||
| " | SFRIC[2] | Contact friction stress | ||||
| " | STOT[2] | Contact total stress (pressure plus friction) | ||||
| " | SLIDE | Contact sliding distance | ||||
| " | GAP | Contact gap distance | ||||
| " | CNOS | Total number of contact status changes during substep |
For MPC-based contact definitions, the value of STAT can be negative. This indicates that one or more contact constraints were intentionally removed to prevent over-constraint. STAT = -3 is used for MPC bonded contact. STAT = -2 is used for MPC no-separation contact.
For the contact force-based model (used for CONTA177 with KEYOPT(3) = 0 or 4), PRES, SFRIC, and STOT are the contact normal force, contact friction force, and total contact force, respectively.
CONTA177 uses most of the same KEYOPTs that are used by the surface-to-surface contact elements, CONTA172 and CONTA174. KEYOPT(3) and KEYOPT(4) differ from the other contact elements. KEYOPT(8) is ignored for line-to-surface contact. See Element KEYOPTS for a listing of the remaining KEYOPTs.
CONTA177 uses the same real constants used by the surface-to-surface contact elements (CONTA172 and CONTA174), except for the units of FKN, FKT, and TNOP. See Real Constants for a complete list.
Four different scenarios can be modelled by CONTA177:
Contact between one beam (or edge) and the surface of a solid or shell
Internal contact where one beam (or pipe) slides inside another hollow beam (or pipe)
External contact between two beams (or edges) that lie next to each other and are roughly parallel
External contact between two beams (or edges) that cross
KEYOPT(3) controls which of the above scenarios are allowed for the element type, and also controls the contact model used (force-based or traction-based):
Use KEYOPT(3) = 0 for the first three scenarios. The program reports contact force (contact force-based model).
Use KEYOPT(3) = 1 for the first three scenarios. The program reports contact pressure (contact traction-based model).
Use KEYOPT(3) = 2 for all scenarios. The program reports contact pressure (contact traction-based model).
Use KEYOPT(3) = 3 for the fourth scenario. The program reports contact pressure (contact traction-based model).
Use KEYOPT(3) = 4 for the fourth scenarios. The program reports contact force (contact force-based model).
For the contact traction-based model (KEYOPT(3) = 1, 2, or 3), the program determines the area (based on the beam element length and beam section radius) associated with the contact node. When the traction-based model is specified, certain real constants (FKN, FKT, TNOP) and postprocessing items (PRES, TAUR, TAUS, SRIC, and so on) have the same units as in the surface-to-surface contact elements (CONTA172 and CONTA174).
When the force-based model is specified (KEYOPT(3) = 0 or 4), the units of these quantities have a factor of AREA with respect to those used in the traction-based model. For example, contact stiffness FKN has units FORCE/LENGTH for the force-based model, but FORCE/LENGTH3 for the traction-based model. Furthermore, PRES is the contact normal force in the force-based model, but contact pressure in the traction-based model. See the CONTA177 element description for detailed information on the units for these quantities.
Using KEYOPT(4) to Define Contact Detection Algorithm
KEYOPT(4) of CONTA177 controls the contact detection algorithm.
By default (KEYOPT(4) = 0), the conventional nodal detection algorithm is used. The program uses a geometric-based gap function to establish the contact condition. Real constant TOLS is used to add a small tolerance that internally extends the edge of the target surface. TOLS is useful for problems where contact nodes are likely to lie on the edge of the target.
Set KEYOPT(4) = 3 or 4 to use the projection-based contact detection algorithm:
KEYOPT(4) = 3 – Standard surface projection
KEYOPT(4) = 4 – Dual shape function projection
These options enforce a contact constraint on an overlapping region of the contact and target surfaces rather than on individual contact nodes (KEYOPT(4) = 0). The contact penetration/gap is computed over the overlapping region in an average sense. With this method, contact forces do not jump when contact nodes slide off the edge of target surfaces. The real constant TOLS is not used.
Compared to the standard projection contact option (KEYOPT(4) = 3), the dual shape function projection option (KEYOPT(4) = 4) uses a special interpolation function for the discretization of contact traction. This option reduces dependent terms for each contact constraint. The resulting gap function and slip increments are closer to the local geometric gap/slip at contact nodes. It is more efficient in terms of solution performance and memory usage and generally remedies potential overconstraint due to MPC equations.
The following restrictions apply when KEYOPT(4) = 3 or 4:
Only the traction based formulation (KEYOPT(3) = 1) is supported.
Only one target segment interacting with each contact detection point (KEYOPT(14) = 0) is supported.
General contact is not supported.
Beam-to-beam contact is not supported.
Note: The reported contact pressure is an approximated quantity. It is calculated based on approximated contact radius and contact length, which are evaluated using the original configuration of the model. The contact pressure value is output for reference only and might not match the true value that would be calculated for an actual 3D model.
For all contact detection options (KEYOPT(4) = 0, 3, and 4), the contact normal is always perpendicular to the target surface. Smoothing is required and is performed by averaging surface normals connected to the target node. As a result, the variation of the surface normal is continuous over the target surface, which leads to a better calculation of friction behavior and better convergence.
Using KEYOPT(4) to Define a Surface-Based Constraint
When CONTA177 is used as part of a surface-based constraint, the KEYOPT(4) setting determines the type of surface-based constraint (rigid surface, force-distributed, or coupling constraint). The multipoint constraint (MPC) approach (KEYOPT(2) = 2) is typically used to define surface-based constraints.
For the force-distributed constraint and the rigid surface constraint, you can use the Lagrange multiplier method (KEYOPT(2) = 3) as an alternative to the MPC approach.
For more information, see Surface-based Constraints.
For line-to-surface contact, set KEYOPT(11) = 1 to include the shell/beam thickness effect. The thickness effect of underlying beam elements (on the contact side) is accounted for via the contact radius input as real constants R2. If the contact radius is not defined, the program automatically calculates the equivalent radius for each individual contact element based on the associated geometry of underlying elements. The thickness effect of underlying shell elements (on the target side) is also accounted for when KEYOPT(11) =1. For more information, see Using KEYOPT(11).
For beam-to-beam contact, the thickness effect is accounted for through the target and contact radii input as real constants R1 and R2, and KEYOPT(11) is ignored.
KEYOPT(14) allows each contact detection point to interact with multiple target segments simultaneously:
KEYOPT(14) = 0: each contact detection point can interact with only one target segment
KEYOPT(14) = 1: each contact detection point can interact with up to four target segments
KEYOPT(14) = 2: each contact detection point can interact with up to eight target segments
The maximum number of contact interactions allowed at each contact detection point is determined by the KEYOPT(14) and KEYOPT(3) settings, as outlined in the table below.
Table 6.1: Number of Interactions Allowed at Contact Detection Points
| KEYOPT(14) | Parallel or Crossing Beams | KEYOPT(3) | Model | Contact Interactions at Nodes I, J, and K [1] | Contact Interactions at Intersection Point (IP) on a Crossing Beam Element [2] |
|---|---|---|---|---|---|
| KEYOPT(14) = 0 | Parallel beams |
KEYOPT(3) = 0 KEYOPT(3) = 1 |
Force-based Traction-based | 1 | 0 |
| All beam scenarios |
KEYOPT(3) = 2 |
Traction-based | 1 | 1 | |
| Crossing beams |
KEYOPT(3) = 3 KEYOPT(3) = 4 |
Traction-based Force-based | 0 | 1 | |
| KEYOPT(14) = 1 | Parallel beams |
KEYOPT(3) = 0 KEYOPT(3) = 1 |
Force-based Traction-based | 4 maximum | 0 |
| All beam scenarios |
KEYOPT(3) = 2 |
Traction-based | 4 maximum | 4 maximum | |
| Crossing beams |
KEYOPT(3) = 3 KEYOPT(3) = 4 |
Traction-based Force-based | 0 | 4 maximum | |
| KEYOPT(14) = 2 | Parallel beams |
KEYOPT(3) = 0 KEYOPT(3) = 1 |
Force-based Traction-based | 8 maximum | 0 |
| All beam scenarios |
KEYOPT(3) = 2 |
Traction-based | 8 maximum | 8 maximum | |
| Crossing beams |
KEYOPT(3) = 3 KEYOPT(3) = 4 |
Traction-based Force-based | 0 | 8 maximum |
To model beam-to-beam or edge-to-edge contact, the contact/target surface is assumed to be the surface of a cylinder. For a general beam cross section other than the circular section, you need to estimate an equivalent circular radius. Follow these guidelines to define the equivalent radius:
Determine the smallest cross section along the beam axis.
Determine the largest circle embedded in that cross section.
The associated target segment elements TARGE170 are either LINE or PARA segment types. Use the first real constant, R1, to define the equivalent radius on the target side. Use the second real constant, R2, to define the equivalent radius on the contact side.
In a general contact definition, the equivalent beam radius is specified via SECTYPE and SECDATA commands instead of using real constants. For more information, see the discussion on applying surface geometry in a general contact definition.
For both pair-based contact and general contact, if the contact radius and/or target radius are not defined, the program automatically calculates the equivalent radius for each individual contact/target element based on the associated geometry of underlying elements. In this case, the equivalent radius may vary within a contact pair or within a general contact surface.
For CONTA177, the contact normal is uniquely defined and is perpendicular to the target surfaces. Real constant TOLS is used to add a small tolerance that will internally extend the edge of the target surface. TOLS is useful for problems where contact nodes are likely to lie on the edge of the target (as at symmetry planes or for models generated in a node-to-node contact pattern). In these situations, the contact node may repeatedly slip off the target surface and be completely out of contact, resulting in convergence difficulties from oscillations.
Units for TOLS are percent (1.0 implies a 1.0% increase in the target edge length). A small value of TOLS will usually prevent this situation from occurring. The default value is 2 for both small deflection (NLGEOM,OFF) and large deflection (NLGEOM,ON).