7.2. Example: Unbalance Harmonic Analysis

7.2.1. Problem Description

The structure is a two-spool rotor on symmetric bearings. Both spools have two rigid disks. The inner spool rotates at up to 14,000 RPM and the outer spool rotates 1.5 times faster.

Disks are not visible in the plot because they are MASS21 elements.

7.2.2. Problem Specifications

The unbalance is located on the second disk of the inner spool and harmonic response is calculated.

Outputs are as follows:

Amplitude at nodes 7 and 12 as a function of the frequency
Orbit plot at a given frequency
Animation of the whirl at a given frequency

7.2.3. Input for the Analysis

Use this input file to perform the example unbalance harmonic analysis of rotating structure using a stationary reference frame.

/batch,list
/title, twin spools - unbalance (inner spool) response 
/PREP7
mp,EX  ,1,2.1e+11
mp,DENS,1,7800
mp,PRXY,1,0.3
! shaft
et,1,188,,,2
sectype,1,beam,csolid
secdata,0.01524,32
sectype,2,beam,ctube
secdata,0.0254,0.03048,32
! disks
et,2,21
r,3,10.51,10.51,10.51,8.59e-2,4.295e-2,4.295e-2
r,4,7.01 ,7.01 ,7.01 ,4.29e-2,2.145e-2,2.145e-2
r,5,3.5  ,3.5  ,3.5  ,2.71e-2,1.355e-2,1.355e-2
r,6,7.01 ,7.01 ,7.01 ,6.78e-2,3.390e-2,3.390e-2
! bearings
et,3,214,,1
r,7 ,2.63e+7 ,2.63e+7
r,8 ,1.75e+7 ,1.75e+7
r,9 ,0.875e+7,0.875e+7
r,10,1.75e+7 ,1.75e+7
! nodes
n,1
n,2 ,0.0762
n,3 ,0.1524
n,4 ,0.2413
n,5 ,0.32385
n,6 ,0.4064
n,7 ,0.4572
n,8 ,0.508
n,9 ,0.1524
n,10,0.2032
n,11,0.2794
n,12,0.3556
n,13,0.4064
! bearings second nodes
n,101,      ,0.05
n,108,0.508 ,0.05
n,109,0.1524,0.05
! components elements
type,1
secn,1
e,1,2
egen,7,1,1
type,2
real,3
e,2
real,6
e,7
cm,inSpool,elem
type,1
secn,2
e,9,10
egen,4,1,10
type,2
real,4
e,10
real,5
e,12
esel,u,,,inSpool
cm,outSpool,elem
allsel
! bearings
type,3
real,7
e,1,101
real,8
e,9,109
real,9
e,6,13
real,10
e,8,108
! boundary conditions
d,all,ux,,,,,rotx
d,101,all
d,108,all
d,109,all
! unbalance forces (eccentric mass * radius)
f0 = 70e-6
f,7,fy,f0
f,7,fz,,-f0
fini
/SOLU
antype,harmic
synchro,,inSpool
nsubst,500
harfrq,,14000/60  ! implicitly defines OMEGA for Coriolis calculation
kbc,1
dmpstr,0.01
cmomega,inSpool,100.
cmomega,outSpool,150.
coriolis,on,,,on 
solve
fini
! output: amplitude at nodes 7 and 12 as a function of the frequency
/POST26
nsol,2,7,U,Y,UY
nsol,3,7,U,Z,UZ
realvar,4,2,,,UYR
realvar,5,3,,,UZR
prod,6,4,4,,UYR_2
prod,7,5,5,,UZR_2
add,8,6,7,,UYR_2+UZR_2
sqrt,9,8,,,AMPL7
!
nsol,2,12,U,Y,UY
nsol,3,12,U,Z,UZ
realvar,4,2,,,UYR
realvar,5,3,,,UZR
prod,6,4,4,,UYR_2
prod,7,5,5,,UZR_2
add,8,6,7,,UYR_2+UZR_2
sqrt,10,8,,,AMPL12
!
/gropt,logy,1
/yrange,1.e-7,1.e-3
plvar,9,10
fini
! output: orbit plot at the given frequency
/POST1
set,1,262
/view,,1,1,1
plorb
! output: animation of the whirl at the given frequency
SET,1,500
!reset for subsequent post processing
/eshape,1
/gline,,-1
plnsol,u,sum
anharm

7.2.4. Analysis Steps

The following table describes the input listing and the general process involved in the example analysis in more detail.

Step	Description	APDL Command(s)
1.	Define material properties.	MP,EX,1,2.1e+11 MP,DENS,1,7800 MP,PRXY,1,0.3
2.	Define element types, sections, real and nodes.	ET,… SECTYPE,… SECDATA,… R,… N,…
3.	Define first component named inSpool.	TYPE,1 SECNUM,1 E,1,2 EGEN,7,1,1 TYPE,2 REAL,3 E,2 REAL,6 E,7 CM,inSpool,ELEM
4.	Define second component named outSpool.	TYPE,1 SECNUM,2 E,9,10 EGEN,4,1,10 TYPE,2 REAL,4 E,10 REAL,5 E,12 ESEL,u,,,inSpool CM,outSpool,ELEM ALLSEL
6.	Define bearing elements.	TYPE,3 REAL,7 E,1,101 REAL,8 E,9,109 REAL,9 E,6,13 REAL,10 E,8,108
5.	Set boundary conditions.	D,...
7.	Define the unbalance forces (eccentric mass * radius) at node 7.	f0 = 70e-6 F,7,FY,f0 F,7,FZ,,-f0
8.	Set the solution options. Harmonic analysis Unbalance on component inSpool 500 substeps Frequency at end of range is 14000/60 Hz Step loading Damping ratio is 1% Rotational velocity of component inSpool Rotational velocity of component outSpool Coriolis force in stationary reference frame Note: The rotational velocities (CMOMEGA) are not applied in the usual way. Rather, the program considers only their direction cosines and the velocity ratio between spools. For more information, see the documentation for the SYNCHRO command.	ANTYPE,HARMIC SYNCHRO,,inSpool NSUBST,500 HARFRQ,,14000/60 KBC,1 DMPSTR,0.01 CMOMEGA,inSpool,100. CMOMEGA,outSpool,150. CORIOLIS,ON,,,ON SOLVE
9.	First output (in POST26). The maximum amplitude of the displacement of nodes 7 (AMPL7) is calculated in variable 9. The maximum amplitude of the displacement of nodes 12 (AMPL12) is calculated in variable 10. Set logY scale. Set a specific scale range in Y. Plot variables 9 and 10.	/POST26 NSOL,2,7,U,Y,UY NSOL,3,7,U,Z,UZ REALVAR,4,2,,,UYR REALVAR,5,3,,,UZR PROD,6,4,4,,UYR_2 PROD,7,5,5,,UZR_2 ADD,8,6,7,,UYR_2+UZR_2 SQRT,9,8,,,AMPL7 ! NSOL,2,12,U,Y,UY NSOL,3,12,U,Z,UZ REALVAR,4,2,,,UYR REALVAR,5,3,,,UZR PROD,6,4,4,,UYR_2 PROD,7,5,5,,UZR_2 ADD,8,6,7,,UYR_2+UZR_2 SQRT,10,8,,,AMPL12 ! /GROPT,LOGY,1 /YRANGE,1.e-7,1.e-3 PLVAR,9,10
10.	Second output (in POST1). Read load step 1 and substep 262 from results file. Change the view. Plot the orbits at each rotating node.	/POST1 SET,1,262 /VIEW,,1,1,1 PLORB
11.	Third output. Display takes dimensions into account. No element outline. Display the displacements as contours. Animate the displays (defined by the last set command and last display command).	/ESHAPE,1 /GLINE,,-1 PLNSOL,U,SUM ANHARM

The outputs of your analysis should match those shown here:

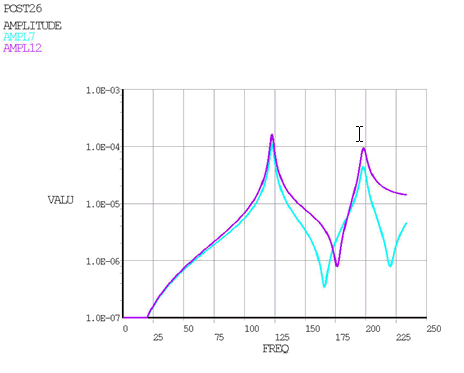
You can obtain the two critical frequencies (at which the amplitudes are largest) via PRCAMP with SLOPE = 1.0.

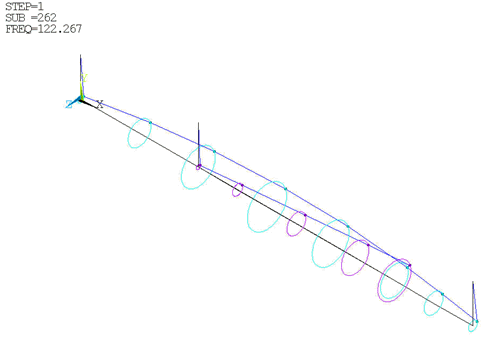
Orbits are represented in different colors. Orbits from the inner spool appear in sky blue, and from the outer spool in purple. Spool lines appear in dark blue.

The following demo is presented as an animated GIF. View online if you are reading the PDF version of the help. Interface names and other components shown in the demo may differ from those in the released product.

The animation of the whirls shown here is the third output resulting from the example harmonic analysis with unbalance.