The model, a cantilevered disk-spindle system, is shown in Figure 7.1: Cantilevered Disk Spindle. The disk is fixed to the spindle with a rigid clamp and is rotating at 0.75*50 Hz. The base excitation is a harmonic force along the negative Y direction, with a frequency of up to 500 Hz.
The geometric properties of the disk are as follows:
| Thickness: 1.0 mm |
| Inner radius: 0.1016 m |
| Outer radius: 0.2032 m |
The geometric properties of the shaft are as follows:
| Length: 0.4064 m |
| Radius: 0.0191 m |
The clamp is modeled with constraint equations. The inertia properties of the clamp are:
| Mass = 6.8748 kg |
| Inertia (XX,YY) = 0.0282 kg.m2 |
| Inertia (ZZ) = 0.0355 kg.m2 |
The material properties for this analysis are as follows
| Young's modulus (E) = 2.04e+11 N/m2 |
| Poisson's ratio (υ) = 0.28 |
| Density = 8030 kg/m3 |
! ** parameters pi = acos(-1) xb = 0.1016 xa = 0.2032 zh = 1.0e-3 rs = 0.0191 ls = 0.4064 d1 = 0.0132 spin = 50*2*pi*0.75 fexcit = 500 /prep7 ! ** material mp,ex,,2.04e+11 mp,nuxy,,.28 mp,dens,,8030. ! ** spindle et,1,188 sectype,1,beam,csolid secd,rs,30 type,1 secn,1 k,1,,,-ls-d1 k,2,,,-d1 l,1,2 lesize,1,,,5 lmesh,all ! ** disk et,2,181 sectype,2,shell secd,zh type,2 secn,2 esize,0.01 cyl4,,,xb,0,xa,360 amesh,all ! ** clamp between disk and spindle et,3,21 r,3,6.8748,6.8748,6.8748,0.0282,0.0282,0.0355 type,3 real,3 n, ncent = node(0,0,0) e,ncent cerig,ncent,node(0,0,-d1),all csys,1 nsel,,loc,x,xb nsel,a,node,,ncent cerig,ncent,all,all allsel csys,0 ! ** constraints = clamp free end nsel,,node,,node(0,0,-ls-d1) d,all,all,0.0 allsel fini ! *** modal analysis in rotation /solu antype,modal modopt,qrdamp,30 mxpand,30 betad,1.e-5 coriolis,on,,,on omega,,,spin acel,,-1 !! generate load vector solve fini ! *** harmonic analysis in rotation /solu antype,harmonic hropt,msup,30 outres,all,none outres,nsol,all acel,0,0,0 kbc,0 harfrq,,fexcit nsubst,500 lvscale,1.0 !! use load vector solve fini ! *** expansion /solu expass,on numexp,all solve ! *** generate response plot /post26 nsol,2,node(0,0,0),U,X,uxTip nsol,3,node(0,0,0),U,Y,uyTip nsol,4,node(0,xa,0),U,Z,uzDisk /gropt,logy,on /axlab,x,FREQUENCIES /axlab,y,DISPLACEMENTS (m) /show,JPEG plvar,2,3,4 EXTREM,2,4,1 /show,CLOSE
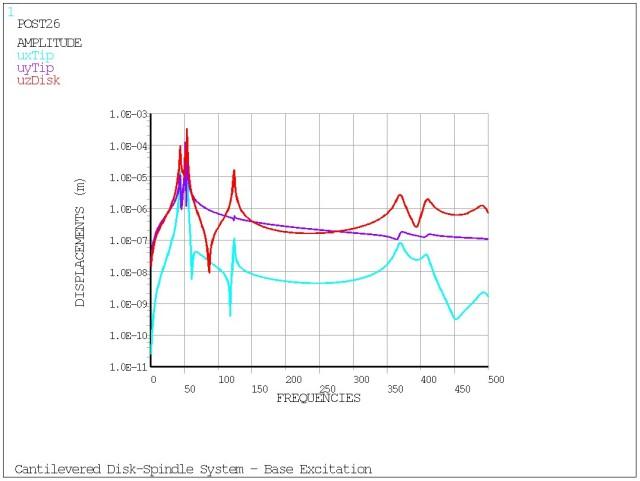
Figure 7.2: Output for the Cantilevered Disk Spindle shows the graph of displacement versus frequency.