This capability provides you with the ability to simultaneously model electromigration, thermomigration, and hydrostatic stress migration resulting from mechanical loading as well as thermal and diffusion stresses. Applications include ion and vacancy transport in solder joints under intense electric current, thermal gradients due to Joule heating, and mechanical stresses.
The following related topics are available:
Table 2.38: Elements Used in Structural-Thermal-Electric-Diffusion Analyses summarizes the elements that you can use to perform a coupled thermal-electric-diffusion analysis. For detailed descriptions of the elements and their characteristics (degrees of freedom, KEYOPT options, inputs and outputs, etc.), see the Element Reference.
For coupled structural-thermal-electric-diffusion analysis, you need to select the UX, UY, UZ, TEMP, VOLT and CONC element degrees of freedom by setting KEYOPT(1) to 100111 for the coupled-field element.
Table 2.38: Elements Used in Structural-Thermal-Electric-Diffusion Analyses
| Elements | Effects | Analysis Types |
|---|---|---|
|
PLANE222 - 4-Node Coupled-Field Quadrilateral PLANE223 - 8-Node Coupled-Field Quadrilateral SOLID225 - 8-Node Coupled-Field Hexahedral SOLID226 - 20-Node Coupled-Field Hexahedral SOLID227 - 10-Node Coupled-Field Tetrahedral |
Thermoelastic (thermal stress and piezocaloric) Thermoelectric (Joule heating; Seebeck, Peltier, and Thomson effects) Diffusion strain Hydrostatic stress migration[a] Temperature dependent material properties, including temperature-dependent saturated concentration (CSAT) Thermomigration Electromigration |
Static Full Transient |
To perform a structural-thermal-electric-diffusion analysis, you need to follow the steps outlined in Performing a Structural-Thermal Analysis, Performing a Thermal-Electric Analysis, Performing a Structural-Diffusion Analysis, Piezoresistive Analysis, Performing a Thermal-Diffusion Analysis, and Performing an Electric-Diffusion Analysis.
Example
The following example demonstrates structural-thermal-electric-diffusion analysis.
Example 2.2: Transient Stress Build-Up Due to Electromigration of Vacancies
/title, Transient stress build-up due to electromigration of vacancies
/prep7
et,1,solid226,100111 ! structural-thermal-electric-diffusion
length=2e-3 ! m
height=0.05e-3 ! m
mp,dxx,1,2.7e-10 ! diffusivity, m^2/s
mp,rsvx,1,5e-7 ! electric resistivity, Ohm*m
mp,kxx,1,390 ! thermal conductivity, W/(m*degC)
mp,c,1,380 ! specific heat, J/(kg*degC)
mp,dens,1,8900 ! density, kg/m^3
mp,ex,1,70e9 ! Young's modulus, Pa
mp,prxy,1,0.35 ! Poisson's ratio
Ze=4*1.6e-19 ! POSITIVE effective charge, C
kB=1.38e-23 ! Boltzmann constant, m^2*kg/(s^2*degK)
Va=1.66e-29 ! atomic volume, m^3
Ceq=6e21 ! equilibrium vacancy concentration, m^(-3)
f=0.6 ! vacancy volume relaxation factor
bet=-Ceq*f*Va*1e3 ! NEGATIVE diffusion expansion coefficient
mp,betx,1,bet ! diffusion expansion -> back-stress
mp,cref,1,1 ! reference concentration for
tb,migr,1,,,1 ! migration model, vacancy flux option
tbdata,2,Va/kB ! stress migration
tbdata,4,Ze/kB ! electromigration
tbdata,8,f ! relaxation factor
ef=5 ! electric field, V/m
v0=ef*length ! corresponding voltage load, V
block,-length,0,0,height,0,height
esize,height
vmesh,all
nsel,s,loc,x,0
d,all,volt,0 ! ground
nsel,s,loc,x,-length
cp,1,volt,all
nd=ndnext(0)
allsel
d,nd,volt,v0 ! voltage load
toffst,273 ! temperature offset from absolute zero to zero
nsel,s,ext
sf,all,conv,5,25 ! convection coefficient, W/(m^2*degC)
nsel,all
d,all,ux,0 ! fully constrained
d,all,uy,0
d,all,uz,0
finish
/solu
antype,trans ! transient analysis
kbc,1
ic,all,conc,1 ! initial concentration
ic,all,temp,25 ! initial temperature
outres,all,all
nsubst,50
time,60*60 ! simulation time, s (1 hour)
autots,off
cnvtol,conc,1,1e-2
nlgeom,on
solve
finish
/post26
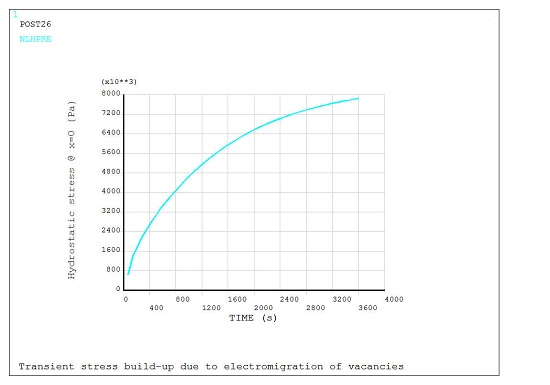
esol,2,length/height,,nl,hpres
/axlab,x,Time (s)
/axlab,y, Hydrostatic stress @ x=0 (Pa)
plvar,2
finish
/post1
set,last,last
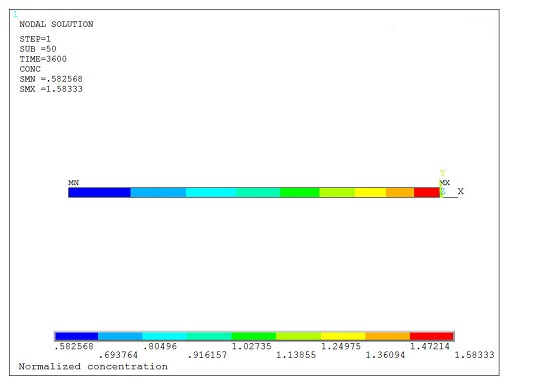
/title, Normalized concentration
plnsol,conc
finish
Hydrostatic stress:
Normalized Concentration: