Use a structural-diffusion analysis to perform diffusion stress analysis and hydrostatic stress migration analysis. Applications of the diffusion stress analysis include hygroscopic swelling of polymers in electronics packages. Applications of the hydrostatic stress migration include stress-assisted diffusion of hydrogen in metals.
For theoretical background, see Structural-Diffusion Coupling in the Theory Reference.
The following related topics are available:
The program includes a variety of elements that you can use to perform a coupled structural-diffusion analysis. Table 2.31: Elements Used in Structural-Diffusion Analyses summarizes them. For detailed descriptions of the elements and their characteristics (degrees of freedom, KEYOPT options, inputs and outputs, etc.), see the Element Reference.
For a coupled structural-diffusion analysis, you need to select the UX, UY, UZ, and CONC element degrees of freedom by setting KEYOPT(1) to 100001 with PLANE222, PLANE223, SOLID225, SOLID226, or SOLID227.
The structural-diffusion KEYOPT settings also make large-deflection, stress-stiffening, and prestress effects available (NLGEOM and PSTRES). (See Structures with Geometric Nonlinearities in the Theory Reference for more information about these capabilities.)
Table 2.31: Elements Used in Structural-Diffusion Analyses
| Elements | Effects | Analysis Types |
|---|---|---|
|
PLANE222 - 4-Node Coupled-Field Quadrilateral PLANE223 - 8-Node Coupled-Field Quadrilateral SOLID225 - 8-Node Coupled-Field Hexahedral SOLID226 - 20-Node Coupled-Field Hexahedral SOLID227 - 10-Node Coupled-Field Tetrahedral |
Diffusion strain Hydrostatic stress migration[a] |
Static Full Transient |
To perform a structural-diffusion analysis:
Select a coupled-field element that is appropriate for the analysis (Table 2.31: Elements Used in Structural-Diffusion Analyses). Use KEYOPT (1) to select the UX, UY, UZ, and CONC element degrees of freedom.
Specify structural material properties:
Specify diffusion material properties:
Specify diffusivity (DXX, DYY, DZZ) (MP).
If working with normalized concentration, specify saturated concentration (CSAT) (MP). For more information, see Normalized Concentration Approach in the Theory Reference.
To account for the diffusion strain effect (or backstress effect when used with electromigration):
To include the hydrostatic stress migration effect:
Specify the atomic volume/Boltzmann constant ratio (Ω/k) using constant C2 (TBDATA) for the migration table, TB,MIGR. Alternatively, you can specify the molar volume/universal gas constant ratio (Vm/R) using the same format. For more information, see Migration Model in the Material Reference.
6. If the diffusivity coefficients depend on temperature and hydrostatic stress as shown in Equation 5–7 of Migration Model in the Material Reference:
Specify the activation energy/Boltzmann constant ratio (Ea/k) using constant C1 (TBDATA) for the migration table, TB,MIGR. Alternatively, you can specify the activation energy/universal gas constant ratio (Ea/R) using the same format.
Specify the volume multiplier (h) using constant C7 (TBDATA)for the migration table, TB,MIGR.
Apply structural and diffusion loads, initial conditions, and boundary conditions:
Structural loads, initial conditions, and boundary conditions include displacement (UX, UY, UZ), force (F), pressure (PRES), and force density (FORC).
Diffusion loads, initial conditions, and boundary conditions include concentration (CONC), diffusion flow rate "force" (RATE), diffusion flux (DFLUX), and diffusing substance generation rate (DGEN).
Specify temperature:
Specify analysis type and solve:
Analysis type can be static or full transient.
For a diffusion strain analysis, you can use KEYOPT(2) to select a strong (matrix) or weak (load vector) structural-diffusion coupling. Strong coupling produces an unsymmetric matrix. In a linear analysis, a strongly coupled response is achieved after one iteration. Weak coupling produces a symmetric matrix and requires at least two iterations to achieve a coupled response.
If using TB,MIGR, the analysis is nonlinear, and at least two iterations are required to achieve a coupled response.
In a nonlinear analysis, set convergence values (CNVTOL) with:
Displacement (U) and force (F) labels
Concentration (CONC) and diffusion flow rate (RATE) labels
For problems having convergence difficulties, activate the line-search capability (LNSRCH).
To prevent unwanted oscillation of concentration outside of the physically meaningful range in a transient analysis that includes PLANE223, SOLID226, or SOLID227 elements, it is recommended that you create the elements without midside nodes and set the damping matrix calculation option to diagonalized (KEYOPT(10) = 1).
Post-process structural and diffusion results:
Structural results include displacements (U), total strain (EPTO), elastic strain (EPEL), thermal strain (EPTH), diffusion strain (EPDI), and stress (S). In an analysis with material or geometric nonlinearities (NL), structural results include plastic yield stress (SEPL), accumulated equivalent plastic strain (EPEQ), accumulated equivalent creep strain (CREQ), plastic yielding (SRAT), and hydrostatic pressure (HPRES).
Diffusion results include concentration (CONC), concentration gradient (CG), and diffusion flux (DF).
This example problem considers a large deflection of a bimorph beam under the concentration load.
The following topics are available:
A beam consists of two materials with different coefficients of diffusion expansion, β1 and β2, and is initially at a reference concentration Cref of 0 kg/m3. The beam is simply supported, and a uniform normalized concentration C = 1 is applied to both surfaces (Figure 2.90: Bimorph Beam Problem Sketch). The beam is expected to undergo a large lateral deflection, so geometric nonlinearities are enabled (NLGEOM,ON).
The solution of the problem requires a coupled structural-diffusion analysis with large-deflection effects, and therefore requires an iterative solution. Since the problem is symmetric, only one-half of the beam is modeled. A convergence criteria for force is specified with a tight tolerance to obtain a converged large-deflection solution.
| Material Properties | Geometric Properties | Loading | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
For material 1:
For material 2:
|
|
|
The beam deformation is shown in Figure 2.91: Bimorph Beam Deformation.
The command listing below demonstrates the problem input. Text prefaced by an exclamation point (!) is a comment.
/TITLE, STRUCTURAL-DIFFUSION ANALYSIS OF A BIMORPH BEAM /nopr /PREP7 ANTYPE,STATIC ! COUPLED FIELD STATIC ANALYSIS NLGEOM,ON ! LARGE DEFLECTION ET,1,PLANE223,100001,,0 ! STRUCTURAL--DIFFUSION, PLANE STRESS MP,EX,1,15E9 ! YOUNG'S MODULUS, PA MP,EX,2,4E9 MP,PRXY,1,0.3 ! POISSON'S RATIO MP,PRXY,2,0.3 MP,BETX,1,14.5E-4 ! DIFFUSION EXPANSION, M3/KG MP,BETX,2,2.5E-4 MP,DXX,1,5e-13 ! DIFFUSIVITY, M2/S MP,DXX,2,3e-13 MP,CSAT,1,7 ! SATURATED CONCENTRATION, KG/M3 MP,CSAT,2,16 K,1 ! DEFINE GEOMETRY K,2,5 KGEN,3,1,2,1,,.05 L,1,2 *REPEAT,3,2,2 LESIZE,ALL,,,5 A,1,2,4,3 AATT,2 A,3,4,6,5 ESIZE,,1 AMESH,ALL NSEL,S,LOC,X,0 NSEL,R,LOC,Y,.05 D,ALL,UY NSEL,S,LOC,Y,.1 D,ALL,CONC,1.0 ! APPLY TOP SURFACE CONCENTRATION (NORMALIZED) NSEL,S,LOC,Y,0 D,ALL,CONC,1.0 ! APPLY BOTTOM SURFACE CONCENTRATION (NORMALIZED) NSEL,S,LOC,X,5 DSYM,SYMM,0,X NSEL,ALL FINISH /SOLU CNVTOL,F,,,,0.1 ! CONVERGENCE BASED ON FORCE ONLY SOLVE FINISH /POST1 SET,1 /DSCALE,1,1 ! TRUE SCALING OPTION PLDISP,1 ! DISPLAY DEFLECTED AND UNDEFLECTED SHAPE NSEL,S,LOC,X,5 NSEL,R,LOC,Y,.05 PRNSOL,U,COMP ! PRINT DISPLACEMENTS FINISH
This example uses structural-diffusion analysis to model hydrogen migration in an axisymmetric tensile test specimen.
The following related topics are available:
A steel tensile specimen is 20 mm in diameter at the end and necks down to 14 mm diameter in the center. An axisymmetric model with half symmetry is used. The specimen is subjected to a tension stress of 1000 MPa at the 20 mm diameter end and constrained axially at the symmetry plane.
The gas properties are those of hydrogen in steel at 800 °C. A normalized concentration of 1.0 is specified at the symmetry plane.
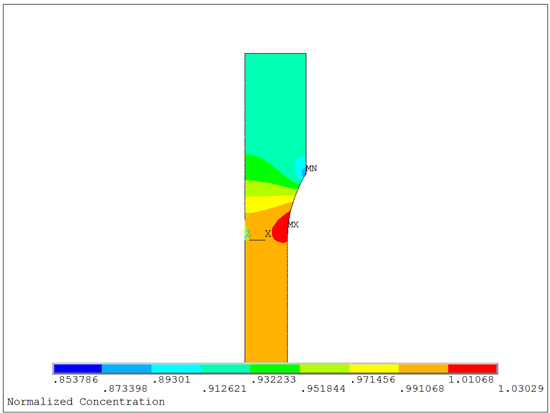
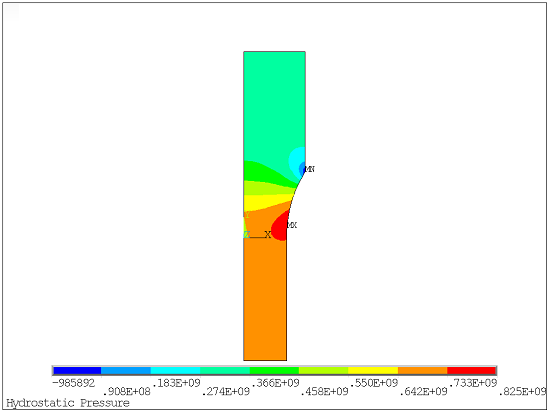
A steady-state analysis produces a normalized concentration distribution matching the distribution of hydrostatic stress, showing that hydrogen will migrate to regions of high tensile stress.
The numerical results at the end of the simulation are shown in the following figures:
The command text below demonstrates the problem input. All text prefaced with an exclamation point (!) is a comment.
/title, Hydrogen migration in an axisymmetric tensile test specimen
/prep7
mp,ex,1,0.2e12 ! Modulus of elasticity Pa
mp,nuxy,1,0.3 ! Poisson's ratio
mp,dxx,1,7.5e-7 ! Diffusivity m^2/s
mp,csat,1,0.15 ! Saturated concentration mol/(m^3-Pa^0.5) at 800 degC
Ea=10100 ! Ea - activation energy J/mol
R=8.314 ! R - universal gas constant J/mol/degK
Vh=1.85e-6 ! Vh - molar volume of hydrogen m^3/mol
tb,migr,1 ! Migration model
tbdata,1,Ea/R,Vh/R
k,1,7e-3 ! Build the model
local,11,1,27e-3
k,2,20e-3,148.2
l,1,2
csys,0
k,3,10e-3,30e-3
k,4,0,30e-3
k,5,0,10.5e-3
k,6,0,0
k,7,0,-20e-3
k,8,7e-3,-20e-3
l,2,3
l,3,4
l,4,5
l,5,6
l,6,7
l,7,8
l,8,1
l,6,1
l,5,2
lsel,s,,,1,5,4
lsel,a,,,9,10
al,all
lsel,s,,,2,4,1
lsel,a,,,10
al,all
lsel,s,,,6,9,1
al,all
lsel,all
! Use spacing ratio to create a refined mesh at the stress concentration
lesize,1,,,20,10
lesize,5,,,20,.1
lesize,9,,,20,.1
lesize,10,,,20,.1
lesize,6,,,20,10
lesize,7,,,20,.1
lesize,8,,,20,.1
lesize,2,,,10,10
lesize,3,,,20,10
lesize,4,,,10,.1
et,1,223,100001,,1 ! PLANE223; structural-diffusion; axisymmetric
mshape,0,2D
mshkey,1
amesh,all
finish
/solu
nsel,s,loc,x,0
d,all,ux,0 ! Constrain axis of symmetry
nsel,s,loc,y,-20e-3 ! Constrain transverse symmetry plane
d,all,uy,0
d,all,conc,1 ! Normalized concentration at transverse plane
nsel,s,loc,y,30e-3
sf,all,pres,-1e9 ! Load specimen in tension
nsel,all
bf,all,temp,800
toff,273
nlgeom,on
time,1
solve
finish
/post1
set,last
/title,Normalized Concentration
plnsol,conc ! Plot normalized concentration
/title,Hydrostatic Stress
plnsol,nl,hpres ! Plot hydrostatic stressAnother structural-diffusion analysis example is found in the Mechanical APDL Verification Manual: