The following complete analysis examples, including command input, are presented here:
For additional examples of a rotating structure analysis using a rotating reference frame, see the following test cases in the Mechanical APDL Verification Manual:
See also:
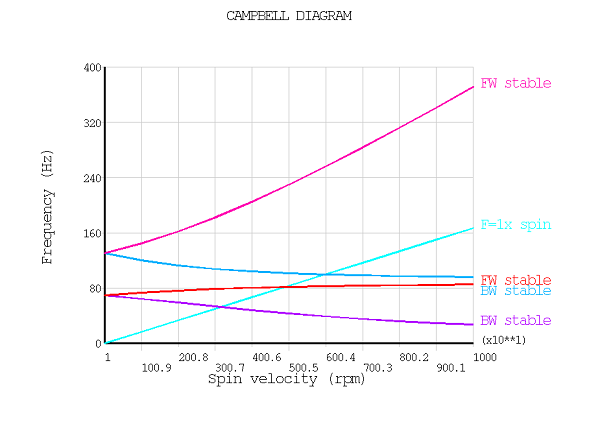
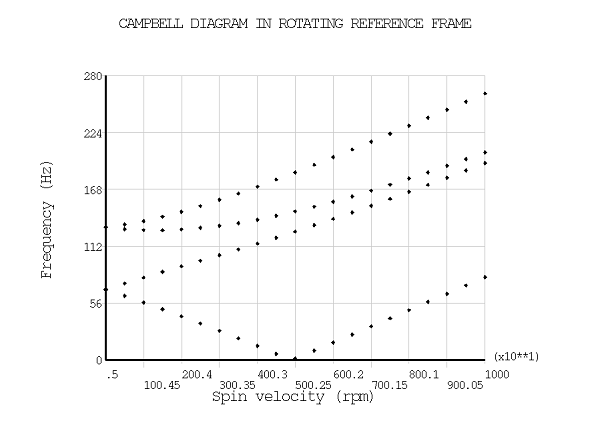
The following example presents a Campbell diagram analysis of a Jeffcott rotor, first in a stationary reference frame (SRF) and then in a rotating reference frame (RRF). It demonstrates the relationship between RRF and SRF frequencies.
The model is a massless rigid rotating shaft supported at its ends by identical bearings (COMBI214). A disk is mounted on the shaft and modelled with a point mass element (MASS21) located at 0.2 m from its end. The shaft is modeled using constraint equations (CERIG command). The rotational velocity varies between 0 rpm and 10,000 rpm along the Z axis.

Inertia properties of the mass:
| Mass = 25 kg |
| Inertia (XX,YY) = 5 kg·m2 |
| Inertia (ZZ) = 10 kg·m2 |
Shaft length: 1 m
Bearing stiffness: 4e+6 N/m
/title, Campbell Diagram Analysis of Jeffcott Rotor ! ** parameters mass = 25 iz = 10 ix = 5 iy = 5 k = 4e+6 pi = acos(-1) ratio = pi/30 omend = ratio*10000 /prep7 n,1,0,0,0 n,2,0,0,1 n,3,0,0,0.2 et,1,mass21 ! fake mass for CERIG 6 DOFs r,1 type,1 real,1 e,1 e,2 et,2,mass21 r,2,mass,mass,mass,ix,iy,iz type,2 real,2 e,3 cerig,3,all,all n,100,,,0 n,110,,,1 et,3,combi214 ! bearing r,3,k,k type,3 real,3 e,100,1 e,110,2 d,all,uz,0 d,all,rotz,0 d,100,all,0 d,110,all,0 finish ! *** Multistep modal analysis in SRF nbp2 = 10 domg2 = omend/nbp2 *dim,omg2,array,nbp2+1 *do,iloop,1,nbp2 omg2(iloop+1) = omg2(iloop) + domg2 *enddo omg2(1) = domg2*1e-2 /solu antype,modal modopt,damp,8 mxpand,8 coriolis,on,,,on *do,iloop,1,nbp2+1 omega,,,omg2(iloop) solve *enddo finish ! ** Campbell in SRF /post1 /show,png,rev /yrange,0,400 plcamp,,1,rpm prcamp,,1,rpm /show,close *dim,FRQ_SRF,ARRAY,4 *do,iloop,1,4 *get,FRQ_SRF(iloop),CAMP,iloop,FREQ,nbp2+1 *enddo finish ! *** Multistep modal analysis in RRF nbp = 20 domg = omend/nbp *dim,omg,array,nbp+1 *do,iloop,1,nbp omg(iloop+1) = omg(iloop) + domg *enddo omg(1) = domg*1e-2 /solu antype,modal modopt,damp,8 mxpand,8 coriolis,on *do,iloop,1,nbp+1 omega,,,omg(iloop) solve *enddo finish ! ** Campbell diagram in RRF /post1 /show,png,rev /yrange,0,280 /gthk,curve,-1 ! no curve - only markers /psymb,mark,4 ! marker size *do,iloop,1,6 /gmarker,iloop,3 ! marker type *enddo plcamp,,,rpm prcamp,,,rpm /show,close *dim,FRQ_RRF,ARRAY,4 *do,iloop,1,4 *get,FRQ_RRF(iloop),CAMP,iloop,FREQ,nbp+1 *enddo finish ! ** Compare SRF and RRF frequencies at maximum spin frend = omend/(2*pi) *dim,FRQ_SRF_INRRF,ARRAY,4 FRQ_SRF_INRRF(1) = abs(FRQ_SRF(2) - frend) FRQ_SRF_INRRF(2) = FRQ_SRF(1) + frend FRQ_SRF_INRRF(3) = abs(FRQ_SRF(4) - frend) FRQ_SRF_INRRF(4) = FRQ_SRF(3) + frend *status,FRQ_SRF *status,FRQ_RRF *status,FRQ_SRF_INRRF
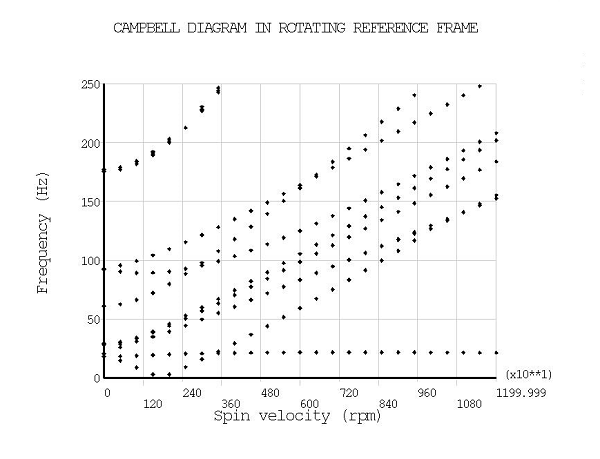
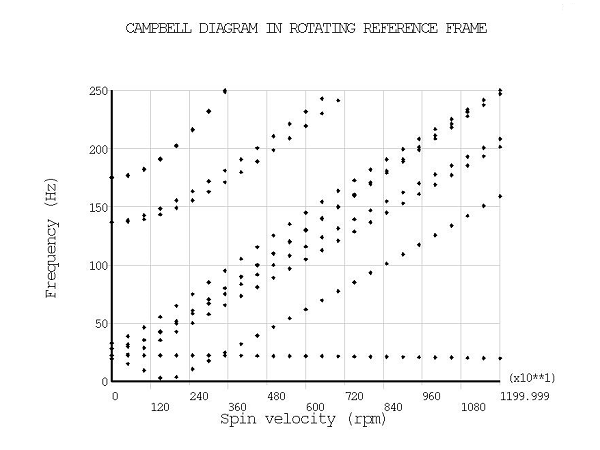
The outputs for this analysis are shown in the figures below.
Figure 5.3: Relationship Between SRF and RRF Frequencies
PARAMETER STATUS- FRQ_SRF ( 21 PARAMETERS DEFINED)
(INCLUDING 2 INTERNAL PARAMETERS)
LOCATION VALUE
1 1 1 27.1023115
2 1 1 85.1999476
3 1 1 95.8462296
4 1 1 371.081927
PARAMETER STATUS- FRQ_RRF ( 21 PARAMETERS DEFINED)
(INCLUDING 2 INTERNAL PARAMETERS)
LOCATION VALUE
1 1 1 81.4667190
2 1 1 193.768978
3 1 1 204.415260
4 1 1 262.512896
PARAMETER STATUS- FRQ_SRF_INRRF ( 21 PARAMETERS DEFINED)
(INCLUDING 2 INTERNAL PARAMETERS)
LOCATION VALUE
1 1 1 81.4667190
2 1 1 193.768978
3 1 1 204.415260
4 1 1 262.512896
The following example from the reference [Friswell et al.] shows a Campbell diagram analysis in the rotating reference frame of an asymmetric rotor carrying two disks, as shown in Figure 5.4: Asymmetric Rotor.
The model is an asymmetric shaft (BEAM188) defined by its cross-section and inertias supported at its ends by identical bearings (COMBI214). The disks are modeled with two point-mass elements (MASS21) located at 0.5 m and 1 m.
The undamped system is studied first, then damping is introduced in the bearings.
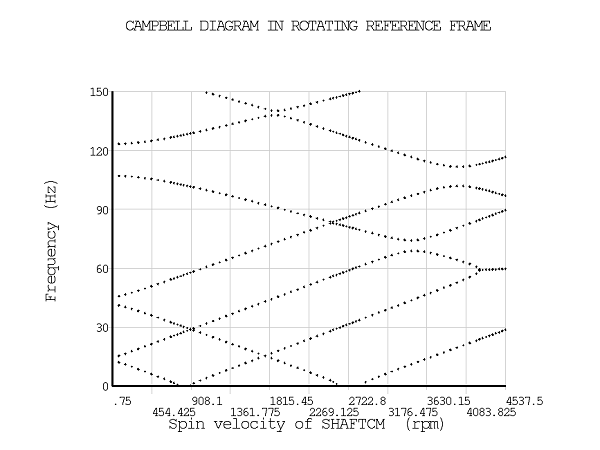
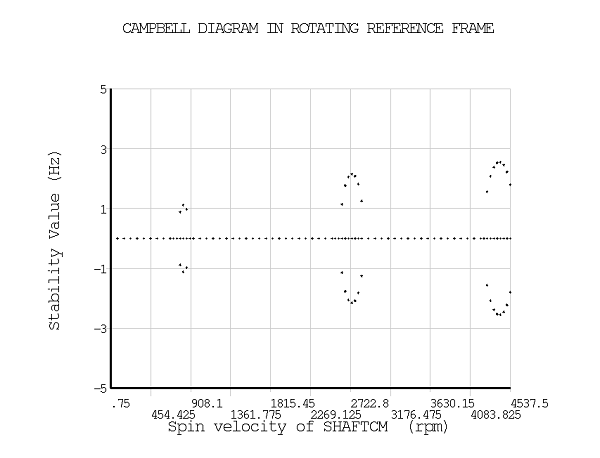
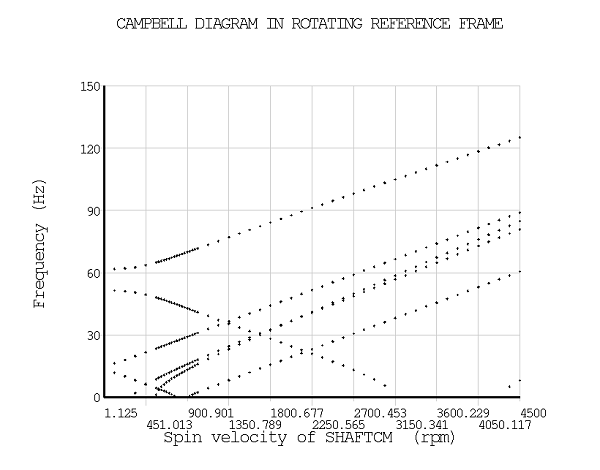
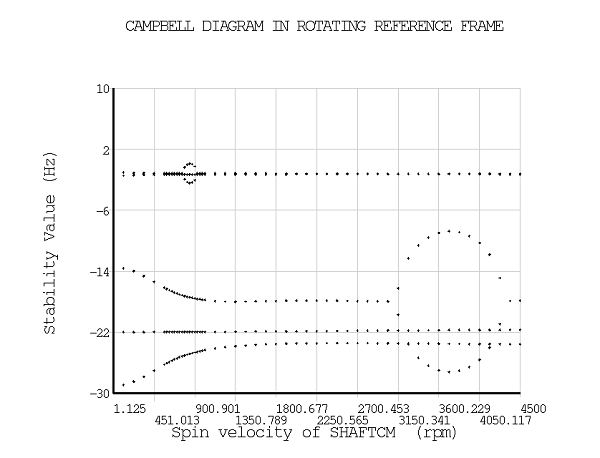
The rotational velocity varies between 0 rpm and 4500 rpm. The evolution of the frequencies and of the stability values are plotted for both undamped and damped systems (PLCAMP). To obtain a more precise shape of the curves around the instability regions, more points are requested by specifying a smaller rotational velocity increment.
Only the shaft and disks are rotating, and the bearings are stationary. Bearing
damping thus introduces rotating damping terms in the rotating reference frame
analysis (RotDamp = ON on the CORIOLIS
command).
Friswell, M., Penny, J., Garvey, S., and Lees, A. Dynamics of Rotating Machines. Cambridge University Press. 2010.
Geometric properties of the shaft:
| Length = 1.5 m |
| Cross sectional area = 2e-3 m2 |
| Moments of area (Iax, Iay) = (4.2043e-7 m4, 2.4112e-7 m4) |
Geometric properties of the disk:
| Diameter_1 = 0.28 m |
| Thickness_1 = 0.07 m |
| Diameter_2 = 0.07 m |
| Thickness_2 = 0.35 m |
Material properties:
| Young’s modulus (E) = 2.11e+11 N/m2 |
| Density = 7810 kg/m3 |
| Poisson's ratio (ν) = 0.3 |
Bearing properties:
| Stiffness (K) = 1e+6 N/m |
| Damping (C) = 5e+3 N·s/m |
/title, Campbell of Non-Axisymmetric Beam Model
! *** parameters
l = 1.5
a = 2e-3
iax = 4.2043e-7
iay = 2.4112e-7
jdummy = 1e-7
e = 211e+9
dens = 7810
nu = 0.3
lld = 0.5
lrd = 1
thkld = 0.07
dld = 0.28
thkrd = 0.07
drd = 0.35
k = 1e+6
c = 5e+3
pi = acos(-1)
ratio = pi/30
omend = 4500
esiz = 0.1
rld = dld/2
mld = pi*thkld*dens*rld**2
idld = mld*(3*rld**2 + thkld**2)/12
ipld = mld*rld**2/2
rrd = drd/2
mrd = pi*thkrd*dens*rrd**2
idrd = mrd*(3*rrd**2 + thkrd**2)/12
iprd = mrd*rrd**2/2
/prep7
! *** geometry
k,1
k,2,,,lld
k,3,,,lrd
k,4,,,l
l,1,2
l,2,3
l,3,4
! *** mesh
lesize,all,esiz
et,1,beam188
mp,ex,1,e
mp,dens,1,dens
mp,nuxy,1,nu
sectype,1,beam,asec
secdata,a,iax,,iay,,jdummy
type,1
mat,1
secnum,1
lmesh,1,3
et,2,mass21
r,2,mld,mld,mld,idld,idld,ipld
type,2
real,2
e,node(0,0,lld)
et,3,mass21
r,3,mrd,mrd,mrd,idrd,idrd,iprd
type,3
real,3
e,node(0,0,lrd)
et,4,combi214
r,4,k,k
type,4
real,4
n,100,0.1
n,104,0.1,,l
e,100,node(0,0,0)
e,104,node(0,0,l)
! *** boundary conditions
d,all,rotz
d,all,uz
d,100,all
d,104,all
! *** component definition
esel,,type,,1,3
cm,shaftcm,elem
allsel
finish
save,case1,db
! *************** Campbell diagram analysis of undamped model
nbp = 60
domg = omend/nbp
nbspins = 73
*dim,omg,array,nbspins+1
*do,iloop,1,nbspins
*if,omg(iloop)+domg,gt,675,and,omg(iloop)+domg,lt,1000,then,
omg(iloop+1) = omg(iloop) + domg/2
*elseif,omg(iloop)+domg,gt,2550,and,omg(iloop)+domg,lt,2925,then,
omg(iloop+1) = omg(iloop) + domg/2
*elseif,omg(iloop)+domg,gt,4200,then,
omg(iloop+1) = omg(iloop) + domg/2
*else
omg(iloop+1) = omg(iloop) + domg
*endif
*enddo
omg(1) = domg*1e-2
/solu
antype,modal
modopt,damp,20
mxpand,20
coriolis,on
*do,iloop,1,nbspins+1
cmomega,shaftcm,,,omg(iloop)*ratio
solve
*enddo
finish
/post1
/show,png,rev
/yrange,0,150
/gthk,curve,-1
/psymb,mark,2
*do,iloop,1,10
/gmarker,iloop,3
*enddo
plcamp,,,rpm,,shaftcm,,yes,yes
prcamp,,,rpm,,shaftcm,,yes,yes
/yrange,-5,5
plcamp,,,rpm,,shaftcm,1,yes,yes
prcamp,,0,rpm,,shaftcm,1,yes,yes
/show,close
finish
/clear,nostart
! ***************** Campbell diagram analysis of damped model
/filname,case2
resume,case1,db
/prep7
rmodif,4,5,C,C ! add damping in bearing
finish
nbp2 = 40
nbp = 52
domg = omend/nbp2
*dim,omg,array,nbp+1
*do,iloop,1,nbp
*if,omg(iloop)+domg,gt,600,and,omg(iloop)+domg,lt,1100,then,
omg(iloop+1) = omg(iloop) + domg/4
*else
omg(iloop+1) = omg(iloop) + domg
*endif
*enddo
omg(1) = domg*1e-2
/solu
antype,modal
modopt,damp,15
mxpand,15
coriolis,on,,,,on ! activate rotating damping effect
*do,iloop,1,nbp+1
cmomega,shaftcm,,,omg(iloop)*ratio
solve
*enddo
finish
/post1
/show,png,rev
/yrange,0,150
/gthk,curve,-1
/psymb,mark,2
*do,iloop,1,10
/gmarker,iloop,3
*enddo
plcamp,,,rpm,,shaftcm,,yes,yes
prcamp,,,rpm,,shaftcm,,yes,yes
/yrange,-30,10
plcamp,,,rpm,,shaftcm,1,yes,yes
prcamp,,0,rpm,,shaftcm,1,yes,yes
/show,close
finish
Without damping, instability regions are identified based on the sign of the stability value. The stability of the rotor is improved when damping is introduced. The results are shown in the graphs below.
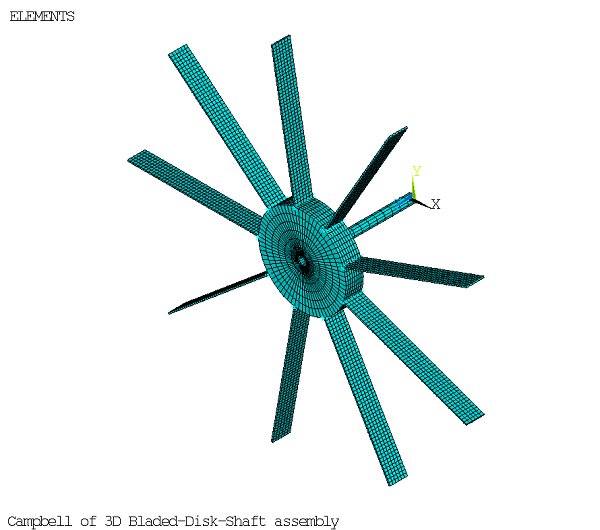
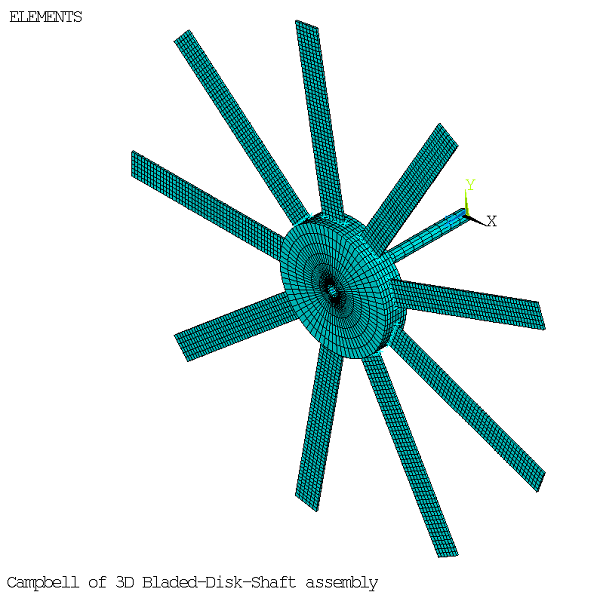
The following example from the reference [Ruffini et al.] presents a Campbell analysis of the 3D bladed shaft-disk assembly shown in Figure 5.9: Bladed Shaft-Disk Assembly (THETA = 0).
The model consists of:
The shaft is fixed at its end. The rotational velocity varies between 0 rpm and 12,000 rpm along the Z axis.
The orientation angle of the blade with respect to the rotational velocity axis (parameter THETA) is first modeled as 0 degrees, then as 90 degrees.
Coriolis effects are activated in the rotating reference frame (CORIOLIS command), and the Campbell procedure (CAMPBELL command) is used to support the Campbell diagram plot.
Ruffini V., Schwingshackl C.W., Green J.S. Prediction Capabilities of Coriolis and Gyroscopic Effects in Current Finite Element Software. Proceedings of the 9th IFToMM International Conference on Rotor Dynamics. Mechanisms and Machine Science, vol 21. Springer, Cham. 2015.
Geometric properties of the shaft:
| Length = 0.25 m |
| Inner diameter = 0.014 m |
| Outer diameter = 0.02 m |
Geometric properties of the disk:
| Outer diameter = 0.2 m |
| Thickness = 0.04 m |
Geometric properties of the blades:
| Length = 0.3 m |
| Thickness = 0.003 m |
| Width = 0.04 m |
Material properties:
| Young’s modulus (E) = 2.07e+11 N/m2 |
| Density = 7800 kg/m3 |
| Poisson's ratio (ν) = 0.3 |
The input listing corresponds to the blade angle THETA = 0.
/title, Campbell of 3D Bladed-Disk-Shaft assembly ! *** PARAMETERS NS = 9 ! number of blades THETA = 0 ! orientation of the blades ! disk Length_D = 0.04 ODiam_D = 0.1*2 ! shaft Length_S = 0.25 IDiam_S = 0.007*2 ODiam_S = 0.01*2 ! blade Length_B = 0.3 Width_B = 0.04 Thick_B = 0.003 ! *** ELEMENT TYPES /PREP7 et,1,185 mp,ex,1,2.07e11 mp,dens,1,7800 mp,nuxy,1,0.3 et,3,170 real,3 et,4,175 keyopt,4,2,2 keyopt,4,9,1 keyopt,4,12,5 et,5,188 mp,ex,5,2.07e11 mp,dens,5,7800 mp,nuxy,5,0.3 sectype,5,beam,ctube secdata,IDiam_S/2,ODiam_S/2,12 et,6,181 mp,ex,6,2.07e11 mp,dens,6,7800 mp,nuxy,6,0.3 sectype,6,shell secdata,Thick_B et,7,170 real,7 et,8,177 keyopt,8,2,2 keyopt,8,9,1 keyopt,8,12,5 ! *** DISK GEOMETRY AND MESH cylind,ODiam_S/2,ODiam_D/2,Length_S-Length_D,Length_S,0,360/NS ndvDR = 6 ! radial ndvDC = 8 ! circumferential ndvDZ = 8 ! along Z LL = (ODiam_D/2) - (ODiam_S/2) lsel,,length,,LL lesize,all,,,ndvDR lsel,,length,,Length_D lesize,all,,,ndvDZ lsel,,length,,Length_D lsel,r,length,,LL lsel,inve lesize,all,,,ndvDC allsel type,1 mat,1 vmesh,1 ! *** BLADE GEOMETRY AND MESH csys,1 *get,maxnod,NODE,0,NUM,MAXD n,maxnod+1,ODiam_D/2,360/NS/2,Length_S-(Length_D/2) n,maxnod+2,(ODiam_D/2)+Length_B,360/NS/2,Length_S-(Length_D/2) n,maxnod+3,ODiam_D/2,360/NS/2,Length_S cs,20,0,maxnod+1,maxnod+2,maxnod+3 wpcsys,,20 wprota,,-THETA rectng, 0,Length_B, Width_B/2,-Width_B/2 ndvBW = 6 ! width divisions ndvBL = 50 ! length divisions lsel,,length,,Length_B lesize,all,,,ndvBL lsla lsel,r,length,,Width_B lesize,all,,,ndvBW csys,1 asel,,loc,x,(ODiam_D+Length_B)/2 type,6 mat,6 secnum,6 amesh,all allsel ! *** CONTACT DISK-BLADE ! contact on blade root csys,1 asel,,LOC,X,(ODiam_D+Length_B)/2 lsla lsel,R,LOC,X,ODiam_D/2 nsll,,1 esln real,3 type,4 esurf allsel ! target on disk csys,1 asel,,LOC,X,ODiam_D/2 nsla,,1 esln type,3 esurf allsel ! *** CONTACT SHAFT-DISK 1/2 (target elements on disk) csys,1 asel,,LOC,X,ODiam_S/2 nsla,,1 esln real,7 type,7 esurf allsel ! *** GENERATE ALL SECTORS csys,1 *get,_node_maxval,node,,num,maxd egen,NS,_node_maxval,all, , , , , , , , , 360/NS /out,scratch esel,,type,,1 nsle nummrg,node allsel /output ! *** SHAFT GEOMETRY AND MESH *get,kpmax,KP,,NUM,MAXD k,kpmax+1 k,kpmax+2,,,Length_S - Length_D k,kpmax+3,,,Length_S ndvS1 = 12 ndvS2 = 4 l,kpmax+1,kpmax+2,ndvS1 l,kpmax+2,kpmax+3,ndvS2 ksel,,kp,,kpmax+1,kpmax+3 lslk type,5 mat,5 secnum,5 lmesh,all ! *** CONTACT SHAFT-DISK 2/2 (contact elements on shaft) kpsel,,kp,,kpmax+3 lslk nsll,,1 esln,,1 real,7 type,8 esurf allsel ! *** BOUNDARY CONDITIONS nsel,,loc,z,0 d,all,all allsel finish ! *** ROTATIONAL VELOCITY TABLE nbstep = 25 spin = 12000 dspin = spin/(nbstep-1) *dim,spins,,nbstep *vfill,spins,ramp,0,dspin RATIO = acos(-1)/30 ! *** CAMPBELL ANALYSIS *do,I,1,nbstep /solu antype,static nlgeom,on autots,on nsub,2,20,1 omega,,,spins(I)*RATIO coriolis,on campbell,rstp outres,all,none outres,nsol,all solve fini /solu antype,static, restart,,,perturb perturb, modal,,, INERKEEP solve, elform modopt,damp,40 mxpand,40 solve fini *enddo ! *** PLOT CAMPBELL DIAGRAM /post1 file,,rstp /show,JPEG /yrange,0,250 /gthk,CURVE,-1 /psymb,MARK,4 *do,ILOOP,1,10 /gmarker,ILOOP,3 *enddo plcamp,off,,RPM,,,,YES,YES prcamp,off,,RPM,,,,YES,YES finish
This example demonstrates the response of a Jeffcott rotor to mass unbalance excitation. It illustrates the equivalence between the static response in the rotating reference frame and the synchronous excitation (SYNCHRO command) in the stationary reference frame.
The model is the same as that shown in Example: Campbell Diagram Analysis of a Jeffcott Rotor, except damping is added in the bearings. This introduces rotating damping terms in the rotating reference frame analysis.
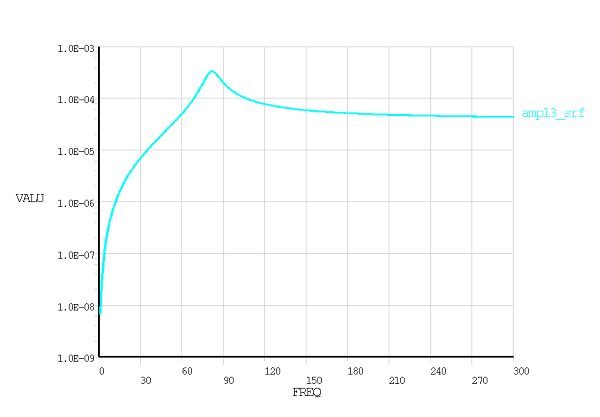
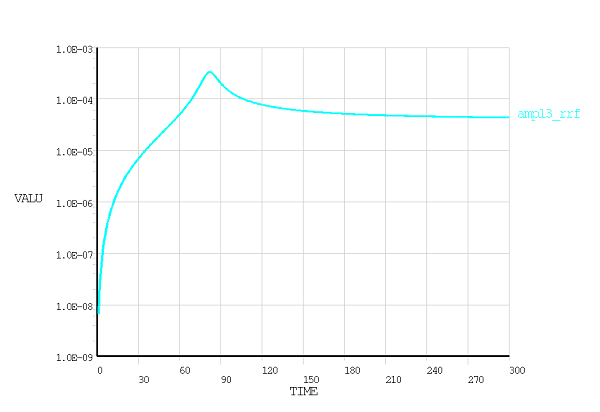
In this example, a force due to a fictive mass unbalance is acting on the mass. The response is calculated over a frequency range of 0 to 300 Hz. POST26 commands are used to output amplitude versus frequency/time graphs.
Inertia properties of the mass:
| Mass = 25 kg |
| Inertia (XX,YY) = 5 kg·m2 |
| Inertia (ZZ) = 10 kg·m2 |
Shaft length: 1 m
Bearing stiffness: 4e+6 N/m
Bearing damping: 1e+3 N·s/m
Excitation force amplitude (mass unbalance multiplied by eccentricity): 1e-3 kg·m
/title, Unbalance Response of a Jeffcott Rotor ! ** parameters mass = 25 iz = 10 ix = 5 iy = 5 k = 4e+6 c = 1e+3 pi = acos(-1) nstep = 300 f0 = 1e-3 /prep7 n,1,0,0,0 n,2,0,0,1 n,3,0,0,0.2 et,1,mass21 ! fake mass for CERIG 6 dofs r,1 type,1 real,1 e,1 e,2 et,2,mass21 r,2,mass,mass,mass,ix,iy,iz type,2 real,2 e,3 cerig,3,all,all n,100,,,0 n,110,,,1 et,3,combi214 ! bearing r,3,k,k,,,c,c type,3 real,3 e,100,1 e,110,2 d,all,uz,0 d,all,rotz,0 d,100,all,0 d,110,all,0 esel,,type,,2 cm,masscm,elem allsel,all finish save ! *** SYNCHRO ANALYSIS IN SRF /solu antype,harmonic hropt,full harfr,0,300 nsubst,nstep kbc,1 f,3,fx,f0 f,3,fy,,-f0 coriolis,on,,,on synchro omega,,,1.0 solve finish /post26 nsol,2,3,u,x,ux3 nsol,3,3,u,y,uy3 realvar,4,2,,,ux3r realvar,5,3,,,uy3r prod,6,4,4,,ux3_2 prod,7,5,5,,uy3_2 add,8,6,7,,ux3_2+uy3_2 sqrt,9,8,,,ampl3_srf *get,max_srf_,VARI,9,EXTREM,VMAX parsav /show,png,rev /gropt,logy,1 /xrange,0,300 plvar,9 finish ! *** STATIC ANALYSIS IN RRF /clear, nostart resume,,db parres dfrq = 1 /solu antype,static kbc,1 coriolis,on,,,,on frq = dfrq *do,iloop,1,nstep /gopr time,frq omg = 2*pi*frq cmomega,masscm,,,omg ftot = f0*omg**2 f,3,fx,ftot solve frq = frq + dfrq *enddo finish /post26 nsol,2,3,u,x,ux3 nsol,3,3,u,y,uy3 prod,6,2,2,,ux3_2 prod,7,3,3,,uy3_2 add,8,6,7,,ux3_2+uy3_2 sqrt,9,8,,,ampl3_rrf *get,max_rrf_,VARI,9,EXTREM,VMAX /show,png,rev /gropt,logy,1 /xrange,0,300 plvar,9 finish ! *** COMPARE MAXIMUM AMPLITUDE *status,PRM_