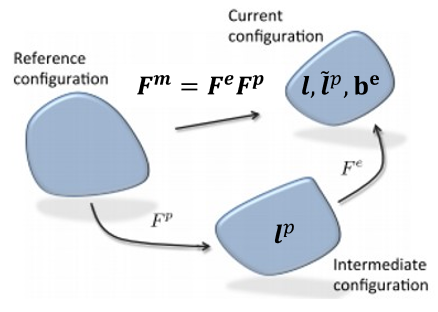
The kinematics of the large-strain hyperelastic plasticity model can be decomposed into elastic and plastic counterparts:

Figure 4.25: Finite-Strain Hyperelastic Plasticity Model Kinematics

The mechanical deformation gradient acting on the material at an integration point is split into an elastic deformation gradient and a plastic deformation gradient :

The multiplicative decomposition assumes the existence of a local unstressed intermediate configuration defined by the plastic deformation gradient. The intermediate configuration is obtained from the deformed configuration by a purely elastic unloading.[1]

For more information about defining the mechanical deformation gradient, see Thermal Deformation in Finite-Strain Material Models.

As in small-strain elastoplasticity models, the stresses acting on the material at integration point are related to the elastic part of deformation. Assuming hyperelastic material formulations, the Kirchhoff stress is obtained from the hyperelastic strain energy potential :

where is the elastic left Cauchy-Green strain, defined as:

The corresponding Cauchy stress is given by:

where .

In single-surface rate-independent plasticity theory, the stresses are bounded by the so-called yield surface . The corresponding admissible stress space is defined by the yield condition. For the finite-strain hyperelastic plasticity model this yield condition is expressed in terms of Kirchhoff stress and additional internal history variables :

The corresponding yield function for a von Mises plasticity model with isotropic hardening reads:

where:

= trace part of the Kirchoff stress

= deviatoric part of the Kirchoff stress

= yield strength

= internal history variable (a scalar with the meaning of equivalent plastic strain)

As in infinitesimal theory, the evolution of plastic deformation is defined by the flow rule. In this context, the spatial velocity gradient (deformed configuration) is used:

The multiplicative split of the deformation gradient results in an additive split of the velocity gradient into an elastic part and a plastic part . Furthermore, the plastic velocity gradient is defined in the intermediate configuration. The plastic velocity gradient can be further decomposed into a symmetric and a skew-symmetric part:

where:

= plastic stretching (rate of plastic deformation) tensor

= plastic spin tensor

The finite-strain plasticity model assumes zero plastic spin:

In the deformed configuration, the finite-strain plastic flow rule is expressed as:

where:

= spatially rotated plastic stretching tensor

= elastic rotation tensor (obtained by polar decomposition of elastic deformation gradient)

= plastic multiplier

= plastic potential

While the plastic multiplier defines the magnitude of plastic deformation, the derivative of the plastic potential with respect to the Kirchhoff stress defines the direction of plastic flow.

The von Mises plasticity model uses an associated flow rule. The plastic potential is chosen to be identical to the yield function. Consequently, the direction of plastic flow is perpendicular to the yield surface.

By using above definition of the plastic flow rule, the evolution of the plastic deformation gradient can be expressed as:

For an isotropic hyperelastic plasticity model, the flow rule can be written in the following equivalent forms:[1]

where is the Lie derivative of with respect to the velocity field . The latter equation is used in the derivation of the stress-calculation algorithm.

The evolution of the internal history variables is generally defined as:

The von Mises model with isotropic hardening has a scalar history variable representing the equivalent plastic strain:

Finally, the irreversible nature of the plastic deformation is represented by the Karush-Kuhn-Tucker loading/unloading conditions:

For small-strain rate-independent analysis, the solution of this general nonlinear problem requires an incremental update of the material state. Starting from a converged step, for which all necessary quantities are known, the stresses, plastic deformations and history variables must be calculated for a given deformation.

At material point, a predictor-corrector scheme is applied. In the elastic predictor step, the so-called trial stress is calculated, assuming that no further plastic flow occurs. If the trial stress satisfies the yield condition, the assumption is valid, and the trial stress is the actual stress. Otherwise, the plastic corrector step is applied.

In this iterative procedure, (referred to as return-mapping or as the stress-return algorithm), the trial stress is returned to the yield surface by developing plastic deformation. As shown in [1], [2], and [3], by using exponential mapping for the flow rule and by introducing logarithmic strains, the classical small-strain closest point return-mapping algorithm [4] can be used for large-strain hyperelastic plasticity models.

The finite-strain plasticity model is a combination of an isotropic hyperelastic model and the isotropic von Mises plasticity model with isotropic hardening.

The isotropic hyperelasticity model is defined via TB,HYPER. The following models are supported:

The von Mises plasticity model with isotropic hardening is defined via TB,PLASTIC or TB,NLISO. The following models are supported:

The finite-strain hyperelastic plasticity model calculates the following output quantities, available via standard postprocessing commands (PRESOL, PRNSOL, PLESOL, PLNSOL, ETABLE, or ESOL):

Table 4.3: Finite Strain Plasticity Output Items

Item	Comp	Description	Value
EPTO		Logarithmic total mechanical strain
EPPL		Logarithmic plastic strain
EPEL		Elastic strain
EPTH		Logarithmic thermal strain
EPTT		Total strain
S		Cauchy stress
SEND	ELASTIC	Elastic energy density[a]
	PLASTIC	Plastic energy density[b]
	ENTO	Total energy density

^[a] Obtained directly from the hyperelastic strain energy potential.

^[b] Updated incrementally using Kirchhoff stress and logarithmic plastic strain.

The following works are referenced or cited in the finite-strain plasticity model documentation: