Fracture parameters are evaluated during the solution phase of the analysis after a substep has converged.
The CINT command initiates the fracture-parameter calculation and specifies the necessary parameters:
- 2.1.1. Step 1: Initiate a New Fracture-Parameter Calculation
- 2.1.2. Step 2: Specify the Type of Fracture-Parameter Calculation
- 2.1.3. Step 3: Define Crack Information
- 2.1.4. Step 4: Specify the Number of Contours (if Needed)
- 2.1.5. Step 5: Define a Crack-Symmetry Condition (if Needed)
- 2.1.6. Step 6: Specify Crack-Surface Traction to be Derived from Initial Stress (if Needed)
- 2.1.7. Step 7: Specify Output Controls
For detailed information about the calculations for specific parameters, see Fracture-Parameter Calculation Types.
Specify the CINT command's NEW option and provide a number to identify the input information for the calculation:
CINT,NEW,n
where n is the number identifying this
fracture-parameter calculation.
Example 2.1: Initiating a New Fracture-Parameter Calculation
CINT,NEW,1 ! Initiate a new fracture-parameter calculation as # 1
Request the calculation for the type of fracture parameter under consideration:
CINT,TYPE,FractureParameter
A fracture-parameter calculation requires the following input:
The crack-tip (front) nodes
The local coordinate systems at the crack tip (front)
Figure 2.1: Schematic Representation of the Crack-Tip Node(s) and Crack-Tip Local Coordinate System (2D and 3D)
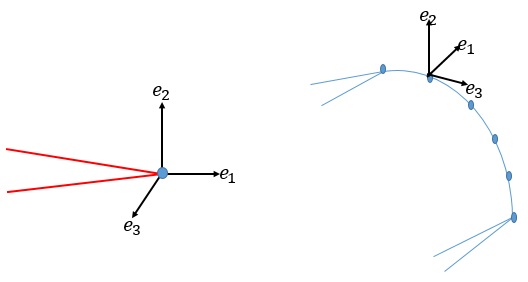
The crack-extension direction (e1), crack-plane normal (e2) at the tip, and the crack-tangent (e3) at the tip together constitute an orthonormal local coordinate system at the crack tip.
Important: The crack-tip nodes and the local coordinate system must be defined correctly. After specifying all parameters, issue the CINT,PLOT command to inspect the local coordinate system.
Two methods are available (via CINT) for specifying the crack-tip node component and one of the vectors of the local coordinate system. (The other vectors are constructed based on the local element and nodal connectivity information.)
Define the crack-tip node component and the crack-plane normal (CINT,CTNC).
This method enables you to specify a crack-tip (front) node component and the normal to the crack plane. Use this method when the crack plane has the same crack normal at all the crack-tip (front) nodes. Generally, this approach applies to both plane 2D crack geometry and 3D flat crack surfaces.
Define the crack-extension node component and crack-extension direction (CINT,CENC).
This method applies to problems where a unique normal may not exist. The method involves defining the crack-extension node component and the crack-extension direction at each crack-tip node location. Use it in any of the following cases:
The crack plane is not flat.
A set of nodes forms the crack tip, as in the case of a collapsed crack-tip mesh.
2D axisymmetric problems exist.
The crack directions are already known.
2.1.3.1. Define the Crack-Tip Node Component and Crack-Plane Normal (CINT,CTNC)
2D crack geometry: Define a crack-tip node component (usually a node located at the crack tip). You can also define a group of nodes around the crack tip, including the node at the crack tip. Mechanical APDL uses this group of nodes as the starting nodes to form the necessary information for the contour integration.
3D flat crack geometry: Define a crack-tip node component that includes all nodes along the crack front. (Only one node can exist at each node location, however.) All nodes in the crack-tip node component must be connectable, and they must form a line (called the crack front) based on the element connectivity associated with it. Mechanical APDL uses the crack front to determine the elements needed for the contour integration. The procedure is similar to 2D crack geometry, and is done through all the nodes along the crack front.
The command syntax is:
CINT,CTNC,Par1
where Par1 is the component name.
After defining the crack-tip node component, use the CINT command's NORM option to define the normal of the crack plane:
CINT,NORM,Par1,Par2
where Par1 is the coordinate system number and
Par2 is the axis of coordinate system defining
the normal of the crack plane.
Mechanical APDL calculates crack-extension vector based on the information provided. The crack-extension vector is taken along the perpendicular direction to the plane formed by the crack-plane normal and the tangent direction of the crack-tip node, and is normalized to a unit vector.
Example 2.4: Defining the Crack-Tip Node Component and Crack-Plane Normal
! local coordinate system LOCAL,11,0,,,, ! select nodes located along the crack front and ! define it as crack front/tip node component NSEL,S,LOC,X,Xctip NSEL,R,LOC,Y,Yctip CM,CRACK_TIP_NODE_CM ! Define a new stress-intensity factors calculation CINT,NEW,1 CINT,TYPE,SIFS CINT,CTNC,CRACK_TIP_NODE_CM CINT,NORM,11,2
Important: Before proceeding, inspect the local coordinate systems at the crack tip to ensure that the crack-extension directions are consistent (CINT,PLOT). If they are inconsistent, you must provide additional information to obtain the correct crack-extension directions. See Inspect the Local Coordinate Systems at the Crack Tip.
The specification of the crack-normal and the crack-tangent (along the crack-front) is sometimes inadequate for evaluating the crack-extension directions.
After defining crack information for fracture-parameter calculation, plot the crack-tip extension directions and normal (CINT,PLOT) before proceeding with the analysis.
Important: If the crack-extension directions are inconsistent, you must provide additional information to obtain the correct crack-extension directions.
You can use either of these methods to provide additional information to control crack-extension directions:
If neither method provides the crack-extension directions needed, use the crack-extension node-component approach (CINT,CENC) to define the local coordinate system.
2.1.3.1.1.1. Specify the Crack-Assist Extension Direction (CINT,EDIR)
The crack-extension directions are primarily calculated using the tangent to the crack-front and the crack-normal. The crack-assist node or the crack-assist extension direction is used only to flip the crack-extension in the appropriate direction.
Issue the CINT,EDIR command to provide an approximate crack-extension direction at any node on the crack front. You can either use the vector form or provide a coordinate system and an axis.
An approximate direction at the reference node provided (optional) is sufficient for Mechanical APDL to properly evaluate the crack-extension directions. If the crack-front extension directions at the crack tips change by more than 180 degrees, the reference node is required.
The command syntax is, respectively:
CINT,EDIR,CS,CSID,AXIS,,REFERENCENODE
CINT,EDIR,COMP,XVAL,YVAL,ZVAL,REFERENCENODE
2.1.3.1.1.2. Specify the Crack-Assist Extension Direction via a Crack-Assist Node (CINT,CTNC)
Alternatively, you can issue the CINT,CTNC command to use the assist node to provide an approximate crack-extension direction:
CINT,CTNC,Par1,Par2,Par3
where Par2 defines the crack-extension
direction calculation-assist node (any node on the open side of the
crack), and Par3 is the crack-front’s
end-node crack-extension direction-override flag.
By default, Mechanical APDL uses the external surface to determine the
crack-extension direction and normal when the crack-tip node meets the
free surface; however, you can use Par3 to
override the default behavior with the calculated coordinate
system.
2.1.3.2. Define the Crack-Extension Node Component and Crack-Extension Direction (CINT,CENC)
Use this method when the crack plane is not flat, or when a set of nodes forms the crack tip, as in the case of a collapsed crack-tip mesh:
Define a node component consisting of one or more nodes forming the crack tip. The node component can have one or more nodes.
Example:
CINT,CENC,ComponentNameIdentify the crack-tip node separately if the node component has more than one node. If a crack-tip node is not identified, the program considers the first node of the node component to be the first node.
Example:
CINT,CENC,ComponentName,Node1Define the crack-extension direction.
Identify the local coordinate system associated with the crack under consideration.
Identify the local axis for the given local coordinate system along which the crack should extend.
Example:
CINT,CENC,ComponentName,Node1,11,2Alternatively, define the crack-extension direction by directly specifying the global X Y and Z components of the crack-extension vector.
Example:
CINT,CENC,ComponentName,Node1,,,compx,compy,compz
Repeat for all node locations along the crack front.
Although Mechanical APDL calculates the local coordinate system at the crack tip to determine stress-intensity factors, it is generally a better practice to use the CINT command's NORM option to help align the calculated normals of the crack-tip nodes.
Example 2.5: Defining the Crack-Extension Node Component and Crack-Extension Direction via Local Coordinate Systems (CINT,CENC)
! Crack-extension node component and ! crack-extension direction specification using local coordinate systems local,11,0,,,, local,12,0,,,, ! … local,n,0,,,, NSEL,S,LOC,X,Xctip1 NSEL,R,LOC,Y,Yctip1 NSEL,R,LOC,Z,Zctip1 CM,CRACK_FRONT_NODE_CM1 NSEL,S,LOC,X,Xctip2 NSEL,R,LOC,Y,Yctip2 NSEL,R,LOC,Z,Zctip2 CM,CRACK_FRONT_NODE_CM2 ! … NSEL,S,LOC,X,Xctipn NSEL,R,LOC,Y,Yctipn NSEL,R,LOC,Z,Zctipn CM,CRACK_FRONT_NODE_CMn CINT,NEW,1 CINT,TYPE,SIFS CINT,CENC,CRACK_FRONT_NODE_CM1,,11,2 CINT,CENC,CRACK_FRONT_NODE_CM2,,12,2 ! … CINT,CENC, CRACK_FRONT_NODE_Cn,,n,2
Example 2.6: Defining the Crack-Extension Node Component and Crack-Extension Direction via Vectors (CINT,CENC)
! Crack-extension node component and ! crack-extension direction specification using vectors NSEL,S,LOC,X,Xctip1 NSEL,R,LOC,Y,Yctip1 NSEL,R,LOC,Z,Zctip1 CM,CRACK_FRONT_NODE_CM1 NSEL,S,LOC,X,Xctip2 NSEL,R,LOC,Y,Yctip2 NSEL,R,LOC,Z,Zctip2 CM,CRACK_FRONT_NODE_CM2 ! … NSEL,S,LOC,X,Xctipn NSEL,R,LOC,Y,Yctipn NSEL,R,LOC,Z,Zctipn CM,CRACK_FRONT_NODE_CMn CINT,NEW,1 CINT,TYPE,SIFS CINT,CENC,CRACK_FRONT_NODE_CM1,,,,Vx1,Vy1,Vz1 CINT,CENC,CRACK_FRONT_NODE_CM2,,,,Vx2,Vy2,Vz2 ! … CINT,CENCOMP,CRACK_FRONT_NODE_Cn,,,,Vxn,Vyn,Vzn
The command syntax for specifying the number of contours is:
CINT,NCON,
n
where n is the number of contours.
For 3D crack geometry, every node along the crack front has the same number of contours.
Example 2.7: Specifying the Number of Contours
CINT,NEW,1 CINT,TYPE,SIFS CINT,CTNC,CRACK_FRONT_NODE_SET,NODE CINT,NCON,6
The command for defining a symmetric condition is:
CINT,SYMM,ON
Example 2.8: Defining a Crack-Symmetry Condition
CINT,NEW,1 CINT,TYPE,SIFS CINT,SYMM,ON ! crack #1 is a symmetrical crack
This command specifies that mesh-independent initial-stress data (if any) are to be converted to crack-surface traction loading:
CINT,CSFL,INIS,STRETo define the mesh-independent initial-stress data, see Mesh-Independent Initial-State Application in the Advanced Analysis Guide. To read the data, issue INISTATE,READ,
Fname,Ext,Path,DOBJ.For a SMART-based crack-growth analysis, the program applies the traction on the growing crack faces after each remeshing automatically.
For more information, see Table 2.2: Material and Load Support for Fracture-Parameter Calculation and Figure 2.2: Superposition Principle: Initial Stress vs. Crack-Face Traction.
Mechanical APDL calculates the fracture parameters during the solution phase of the analysis and stores it in the results file for postprocessing. The output uses all defaults from the OUTRES command.
The command OUTRES,ALL includes CINT command results. To control the output for specific fracture-parameter results only, issue OUTRES,CINT.
Example 2.9: Specifying Output Controls
CINT,NEW,1 CINT,TYPE,SIFS CINT,CTNC,CRACK_TIP_NODE_CM CINT,SYMM,ON CINT,NCON,5 OUTRES,CINT,10 ! Output CINT results every 10 substeps


