The devolatilization law is applied to a combusting particle
when the temperature of the particle reaches the vaporization temperature, , and remains
in effect while the mass of the particle,
, exceeds the
mass of the nonvolatiles in the particle:
(12–105) |
and
(12–106) |
where is the mass fraction of the evaporating/boiling
material if Wet Combustion is selected (otherwise,
). As implied by Equation 12–105, the boiling point,
,
and the vaporization temperature,
, should be set equal to each
other when Law 4 is to be used. When wet combustion is active,
and
refer to the boiling and evaporation temperatures
for the droplet material only.
Ansys Fluent provides a choice of four devolatilization models:
the constant rate model (the default model)
the single kinetic rate model
the two competing rates model (the Kobayashi model)
the chemical percolation devolatilization (CPD) model
Each of these models is described, in turn, in the following sections.
You will choose the devolatilization model when you are setting physical properties for the combusting-particle material in the Create/Edit Materials Dialog Box, as described in Description of the Properties in the User’s Guide. By default, the constant rate model (Equation 12–107) will be used.
The constant rate devolatilization law dictates that volatiles are released at a constant rate [50]:
(12–107) |
| where | |
|
| |
|
| |
|
| |
|
|
The rate constant is defined in the material properties of the combusting
particle(s). The Fluent materials database includes default values
for each of the available combusting particle materials. A representative
value is 12 s–1 derived from the
work of Pillai [519] on coal combustion. Proper
use of the constant devolatilization rate requires that the vaporization
temperature, which controls the onset of devolatilization, be set
appropriately. Values in the literature show this temperature to be
about 600 K [50].
The volatile fraction of the particle enters the gas phase as
the devolatilizing species , defined by you (see Setting Material Properties for the Discrete Phase in the User’s
Guide). Once in the gas phase, the volatiles may react according to
the inputs governing the gas phase chemistry.
The single kinetic rate devolatilization model assumes that the rate of devolatilization is first-order dependent on the amount of volatiles remaining in the particle [36]:
(12–108) |
| where | |
|
| |
|
| |
|
| |
|
| |
|
|
Note that , the fraction of volatiles
in the particle, should be defined using a value slightly in excess
of that determined by proximate analysis. The kinetic rate,
, is defined by input of
an Arrhenius type pre-exponential factor and an activation energy:
(12–109) |
The Fluent materials
database includes default values for the rate constants, and
, for each of the available
combusting particle materials.
Equation 12–108 has the approximate analytical solution:
(12–110) |
which is obtained by assuming that the particle temperature varies only slightly between discrete time integration steps.
Ansys Fluent can also solve Equation 12–108 in conjunction with the equivalent heat transfer equation using a stiff coupled solver. See Including Coupled Heat-Mass Solution Effects on the Particles in the User’s Guide for details.
Ansys Fluent also provides the kinetic devolatilization rate expressions of the form proposed by Kobayashi [316]:
(12–111) |
(12–112) |
where and
are competing rates that may control the devolatilization
over different temperature ranges. The two kinetic rates are weighted
to yield an expression for the devolatilization as
(12–113) |
| where | |
|
| |
|
| |
|
| |
|
|
The Kobayashi model requires input of the kinetic rate parameters, ,
,
, and
, and the yields
of the two competing reactions,
and
. Ansys Fluent uses default values for the yield factors
of 0.3 for the first (slow) reaction and 1.0 for the second (fast)
reaction. It is recommended in the literature [316] that
be set to
the fraction of volatiles determined by proximate analysis, since
this rate represents devolatilization at low temperature. The second
yield parameter,
, should be
set close to unity, which is the yield of volatiles at very high temperature.
Note that in Ansys Fluent, the effect of particle heating rate on evolution of volatile yield is not considered.
By default, Equation 12–113 is integrated in time analytically, assuming the particle temperature to be constant over the discrete time integration step. Ansys Fluent can also solve Equation 12–113 in conjunction with the equivalent heat transfer equation using a stiff coupled solver. See Including Coupled Heat-Mass Solution Effects on the Particles in the User's Guide for details.
In contrast to the coal devolatilization models presented above, which are based on empirical rate relationships, the chemical percolation devolatilization (CPD) model characterizes the devolatilization behavior of rapidly heated coal based on the physical and chemical transformations of the coal structure [183], [184], [218].
During coal pyrolysis, the labile bonds between the aromatic clusters in the coal structure lattice are cleaved, resulting in two general classes of fragments. One set of fragments has a low molecular weight (and correspondingly high vapor pressure) and escapes from the coal particle as a light gas. The other set of fragments consists of tar gas precursors that have a relatively high molecular weight (and correspondingly low vapor pressure) and tend to remain in the coal for a long period of time during typical devolatilization conditions. During this time, reattachment with the coal lattice (which is referred to as cross-linking) can occur. The high molecular weight compounds plus the residual lattice are referred to as metaplast. The softening behavior of a coal particle is determined by the quantity and nature of the metaplast generated during devolatilization. The portion of the lattice structure that remains after devolatilization is are made up of char and mineral-compound-based ash.
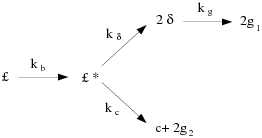
The CPD model characterizes the chemical and physical processes by considering the coal structure as a simplified lattice or network of chemical bridges that link the aromatic clusters. Modeling the cleavage of the bridges and the generation of light gas, char, and tar precursors is then considered to be analogous to the chemical reaction scheme shown in Figure 12.1: Coal Bridge.
The variable represents the original population of labile bridges
in the coal lattice. Upon heating, these bridges become the set of
reactive bridges,
. For the reactive bridges,
two competing paths are available. In one path, the bridges react
to form side chains,
. The side chains may detach from the aromatic
clusters to form light gas,
. As bridges
between neighboring aromatic clusters are cleaved, a certain fraction
of the coal becomes detached from the coal lattice. These detached
aromatic clusters are the heavy-molecular-weight tar precursors that
form the metaplast. The metaplast vaporizes to form coal tar. While
waiting for vaporization, the metaplast can also reattach to the coal
lattice matrix (crosslinking). In the other path, the bridges react
and become a char bridge,
, with the release of an associated light gas product,
. The total population of bridges in the coal lattice
matrix can be represented by the variable
, where
.
Given this set of variables that characterizes the coal lattice
structure during devolatilization, the following set of reaction rate
expressions can be defined for each, starting with the assumption
that the reactive bridges are destroyed at the same rate at which
they are created ():
(12–114) |
(12–115) |
(12–116) |
(12–117) |
(12–118) |
where the rate constants for bridge breaking and gas release
steps, and
, are expressed
in Arrhenius form with a distributed activation energy:
(12–119) |
where ,
, and
are, respectively,
the pre-exponential factor, the activation energy, and the distributed
variation in the activation energy,
is the universal gas constant,
and
is the temperature. The ratio of rate constants,
, is set to
0.9 in this model based on experimental data.
The following mass conservation relationships are imposed:
(12–120) |
(12–121) |
(12–122) |
where is the fraction of broken bridges (
). The initial conditions for this system are given by the following:
(12–123) |
(12–124) |
(12–125) |
(12–126) |
where is the initial
fraction of char bridges,
is the initial
fraction of bridges in the coal lattice, and
is the initial fraction
of labile bridges in the coal lattice.
Given the set of reaction equations for the coal structure parameters,
it is necessary to relate these quantities to changes in coal mass
and the related release of volatile products. To accomplish this,
the fractional change in the coal mass as a function of time is divided
into three parts: light gas (),
tar precursor fragments (
), and char (
). This is accomplished by using the following relationships,
which are obtained using percolation lattice statistics:
(12–127) |
(12–128) |
(12–129) |
The variables ,
,
, and
are the
statistical relationships related to the cleaving of bridges based
on the percolation lattice statistics, and are given by the following
equations:
(12–130) |
(12–131) |
(12–132) |
(12–133) |
is the ratio of bridge mass to site mass,
, where
(12–134) |
(12–135) |
where and
are the side chain and cluster molecular weights
respectively.
is the lattice coordination number,
which is determined from solid-state nuclear magnetic Resonance (NMR)
measurements related to coal structure parameters, and
is
the root of the following equation in
(the total number of bridges
in the coal lattice matrix):
(12–136) |
In accounting for mass in the metaplast (tar precursor fragments), the part that vaporizes is treated in a manner similar to flash vaporization, where it is assumed that the finite fragments undergo vapor/liquid phase equilibration on a time scale that is rapid with respect to the bridge reactions. As an estimate of the vapor/liquid that is present at any time, a vapor pressure correlation based on a simple form of Raoult’s Law is used. The vapor pressure treatment is largely responsible for predicting pressure-dependent devolatilization yields. For the part of the metaplast that reattaches to the coal lattice, a cross-linking rate expression given by the following equation is used:
(12–137) |
where is the amount of mass reattaching to the
matrix,
is the amount of mass in the tar precursor fragments
(metaplast), and
and
are rate expression constants.
Given the set of equations and corresponding rate constants introduced for the CPD model, the number of constants that must be defined to use the model is a primary concern. For the relationships defined previously, it can be shown that the following parameters are coal independent [183]:
,
,
,
,
, and
for the rate constants
and
,
, and
These constants are included in the submodel formulation and are not input or modified during problem setup.
There are an additional five parameters that are coal-specific and must be specified during the problem setup:
initial fraction of bridges in the coal lattice,
initial fraction of char bridges,
lattice coordination number,
cluster molecular weight,
side chain molecular weight,
The first four of these are coal structure quantities that are obtained from NMR experimental data. The last quantity, representing the char bridges that either exist in the parent coal or are formed very early in the devolatilization process, is estimated based on the coal rank. These quantities are entered in the Create/Edit Materials dialog box, as described in Description of the Properties in the User's Guide. Values for the coal-dependent parameters for a variety of coals are listed in Table 12.1: Chemical Structure Parameters for C NMR for 13 Coals.
Table 12.1: Chemical Structure Parameters for C NMR for 13 Coals
|
Coal Type |
|
|
|
|
|
|
Zap (AR) |
3.9 |
.63 |
277 |
40 |
.20 |
|
Wyodak (AR) |
5.6 |
.55 |
410 |
42 |
.14 |
|
Utah (AR) |
5.1 |
.49 |
359 |
36 |
0 |
|
Ill6 (AR) |
5.0 |
.63 |
316 |
27 |
0 |
|
Pitt8 (AR) |
4.5 |
.62 |
294 |
24 |
0 |
|
Stockton (AR) |
4.8 |
.69 |
275 |
20 |
0 |
|
Freeport (AR) |
5.3 |
.67 |
302 |
17 |
0 |
|
Pocahontas (AR) |
4.4 |
.74 |
299 |
14 |
.20 |
|
Blue (Sandia) |
5.0 |
.42 |
410 |
47 |
.15 |
|
Rose (AFR) |
5.8 |
.57 |
459 |
48 |
.10 |
|
1443 (lignite, ACERC) |
4.8 |
.59 |
297 |
36 |
.20 |
|
1488 (subbituminous, ACERC) |
4.7 |
.54 |
310 |
37 |
.15 |
|
1468 (anthracite, ACERC) |
4.7 |
.89 |
656 |
12 |
.25 |
AR refers to eight types of coal from the Argonne premium sample bank [616], [681]. Sandia refers to the coal examined at Sandia National Laboratories [182]. AFR refers to coal examined at Advanced Fuel Research. ACERC refers to three types of coal examined at the Advanced Combustion Engineering Research Center.
The particle diameter changes during devolatilization according to the swelling
coefficient, , which is defined by you and applied in the following relationship:
(12–138) |
| where | |
|
| |
|
|
The term is the ratio of the mass that has been devolatilized to the total volatile
mass of the particle. This quantity approaches a value of 1.0 as the devolatilization law is
applied. When the swelling coefficient is equal to 1.0, the particle diameter stays constant.
When the swelling coefficient is equal to 2.0, the final particle diameter doubles when all of
the volatile component has vaporized, and when the swelling coefficient is equal to 0.5 the
final particle diameter is half of its initial diameter.
Heat transfer to the particle during the devolatilization process includes contributions from convection and radiation (if active):
(12–139) |
where the variables have already been defined for Equation 12–93.
Radiation heat transfer to the particle is included only if you have enabled the P-1 or discrete ordinates radiation heat transfer to particles using the Particle Radiation Interaction option in the Discrete Phase Model Dialog Box.
By default, Equation 12–139 is solved analytically, by assuming that the temperature and mass of the particle do not change significantly between time steps:
(12–140) |
where
(12–141) |
and
(12–142) |
Ansys Fluent can also solve Equation 12–139 in conjunction with the equivalent mass transfer equation using a stiff coupled solver. See Including Coupled Heat-Mass Solution Effects on the Particles in the User’s Guide for details.