VM211

VM211
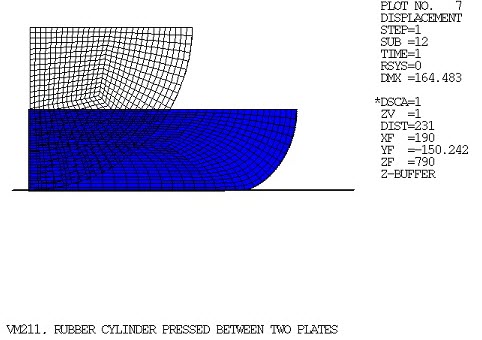
Rubber Cylinder Pressed Between Two Plates

Overview

Reference:

T. Tussman, K-J Bathe, "A Finite Element Formulation for Nonlinear Incompressible Elastic and Inelastic Analysis", Computers and Structures, Vol. 26 Nos 1/2, 1987, pp. 357-409.

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Element Type(s):

2D 4-Node Structural Solid Elements (PLANE182)

2D 8-Node Structural Solid Elements (PLANE183)

3D 8-Node Structural Solid Elements (SOLID185)

3D 20-Node Structural Solid or Layered Solid Elements (SOLID186)

2D 3-Node Surface-to-Surface Contact Elements (CONTA172)

3D 8-Node Surface-to-Surface Contact Elements (CONTA174)

2D Target Segment Elements (TARGE169)

3D Target Segment Elements (TARGE170)

Input Listing:

vm211.dat

Test Case

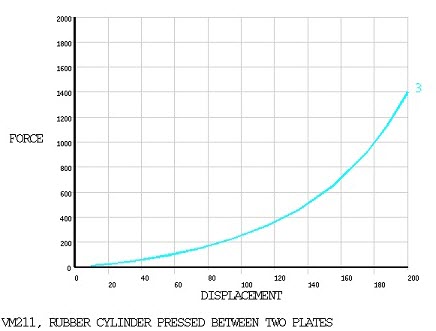
A long rubber cylinder is pressed between two rigid plates using a maximum imposed displacement of δ_max. Determine the force-deflection response.

Figure 333: Rubber Cylinder Problem Sketch

Material Properties

Geometric Properties

Mooney-Rivlin Constants:

C1 = 0.293 MPa

C2 = 0.177 MPa

r = 200 mm

δ_max = 200 mm

Real Constant[1]

FKN = 8

Applicable to CONTA172 and CONTA174.

Analysis Assumptions and Modeling Notes

This test case solves the problem of VM201 using the 2D and 3D rigid target and contact elements. A plane strain solution is assumed based on the geometry of the problem. Due to geometric and loading symmetry, the analysis can be performed using one quarter of the cross section. All nodes on the left edge (X = 0) are constrained, UX = 0. All nodes on the top edge (y = 0) are coupled in UY. An imposed displacement of -0.1 m acts upon the coupled nodes.

The problem is solved in 12 different ways. The first four solutions are performed using the default contact algorithm, the next four are performed using the Lagrange multipliers method (KEYOPT(2) = 3 ) of contact elements, and the final four are performed using the exponential pressure-penetration relationship (KEYOPT(6) = 3):

The lower-order 2D model used PLANE182 with CONTA172 and TARGE169 elements.
The higher-order 2D model used PLANE183 with CONTA172 and TARGE169.
The lower-order 3D model used SOLID185 with CONTA174 and TARGE170.
The higher-order 3D model used SOLID186 with CONTA174 and TARGE170.
The lower-order 2D model used PLANE182 with CONTA172 and TARGE169 and solved using Lagrange multipliers method.
The higher-order 2D model used PLANE183 with CONTA172 and TARGE169 and solved using Lagrange multipliers method.
The lower-order 3D model used SOLID185 with CONTA174 and TARGE170 and solved using Lagrange multipliers method.
The higher-order 3D model used SOLID186 with CONTA174 and TARGE170 and solved using Lagrange multipliers method.
The lower-order 2D model used PLANE182 with CONTA172 and TARGE169 and solved using the exponential pressure-penetration relationship
The higher-order 2D model used PLANE183 with CONTA172 and TARGE169 and solved using the exponential pressure-penetration relationship.
The lower-order 3D model used SOLID185 with CONTA174 and TARGE170 and solved using the exponential pressure-penetration relationship.
The higher-order 3D model used SOLID186 with CONTA174 and TARGE170 and solved using the exponential pressure-penetration relationship.

Results Comparison

		Target[1]	Mechanical APDL	Ratio
PLANE182	Force at Displacement = 0.1 (N)	250.00	243.02	0.972
PLANE182	Force at Displacement = 0.2 (N)	1400.00	1362.08	0.973
PLANE183	Force at Displacement = 0.1 (N)	250.00	244.93	0.980
PLANE183	Force at Displacement = 0.2 (N)	1400.00	1372.60	0.980
SOLID185	Force at Displacement = 0.1 (N)	250.00	241.58	0.966
SOLID185	Force at Displacement = 0.2 (N)	1400.00	1359.44	0.971
SOLID186	Force at Displacement = 0.1 (N)	250.00	252.69	1.011
SOLID186	Force at Displacement = 0.2 (N)	1400.00	1399.81	1.000
With KEYOPT (2) = 3 of CONTA172 (dropped midside nodes)
PLANE182	Force at Displacement = 0.1 (N)	250.00	252.57	1.010
PLANE182	Force at Displacement = 0.2 (N)	1400.00	1406.84	1.005
With KEYOPT (2) = 3 of CONTA172
PLANE183	Force at Displacement = 0.1 (N)	250.00	256.10	1.024
PLANE183	Force at Displacement = 0.2 (N)	1400.00	1415.80	1.011
With KEYOPT (2) = 3 of CONTA174 (dropped midside nodes)
SOLID185	Force at Displacement = 0.1 (N)	250.00	251.46	1.006
SOLID185	Force at Displacement = 0.2 (N)	1400.00	1400.48	1.000
With KEYOPT (2) = 3 of CONTA174
SOLID186	Force at Displacement = 0.1 (N)	250.00	255.65	1.023
SOLID186	Force at Displacement = 0.2 (N)	1400.00	1416.53	1.012
With KEYOPT (6) = 3 of CONTA172 (dropped midside nodes)
PLANE182	Force at Displacement = 0.1 (N)	250.00	242.88	0.972
PLANE182	Force at Displacement = 0.2 (N)	1400.00	1366.14	0.976
With KEYOPT (6) = 3 of CONTA172
PLANE183	Force at Displacement = 0.1 (N)	250.00	244.33	0.977
PLANE183	Force at Displacement = 0.2 (N)	1400.00	1357.87	0.970
With KEYOPT (6) = 3 of CONTA174 (dropped midside nodes)
SOLID185	Force at Displacement = 0.1 (N)	250.00	246.01	0.984
SOLID185	Force at Displacement = 0.2 (N)	1400.00	1363.66	0.974
With KEYOPT (6) = 3 of CONTA174
SOLID186	Force at Displacement = 0.1 (N)	250.00	254.11	1.016
SOLID186	Force at Displacement = 0.2 (N)	1400.00	1405.32	1.004

Determined from graphical results. See T. Tussman, K-J Bathe, "A Finite Element Formulation for Nonlinear Incompressible Elastic and Inelastic Analysis", pg. 385, fig. 6.14.

Figure 334: Displaced Shape

Figure 335: Force vs. Displacement