VM210
VM210
Pyramid Validation of Tetrahedron to Hexahedron
Overview
Test Case
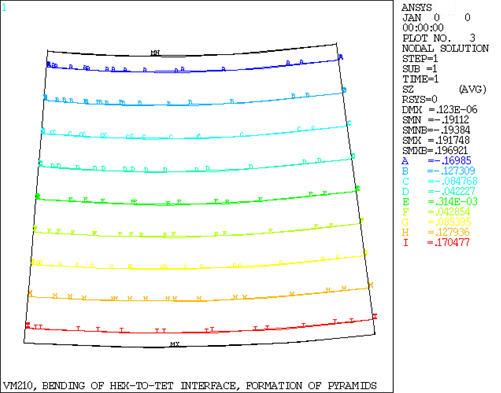
For an elastic beam subjected to pure bending, validate the use of pyramids in a tetrahedron to hexahedron interface. Find the axial stress at the top, midplane, and bottom surfaces.
| Material Properties | Geometric Properties | Loading | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Analysis Assumptions and Modeling Notes
The problem is solved in two different ways:
The model is generated using the block primitive which is divided into 8 sub-blocks. The pyramid interface is created by meshing the hexahedra first, followed by the tetrahedra. The working plane describes the hex-tet interface region.
Full displacement constraints placed upon three corners in the model midplane does not allow generation of significant reaction forces. A pure bending condition is created by the application of a pressure gradient on the faces of elements lying in the z = 0 and z = L planes. The linear gradient varies from -0.18979 on the bottom to 0.18979 on the top.
σz = (Mzy) / (Ic)
where
| σZ = stress in z-direction |
| Mz = effective moment, z-direction |
| y = distance from neutral surface |
| Ic = second moment of area about the horizontal centroidal axis |
|
|
Results Comparison
| Target | Mechanical APDL | Ratio | |
|---|---|---|---|
| SOLID95 | |||
| StressZ , Top (AVG) | -0.1898 | -0.1899 | 1.001 |
| StressZ , Neutral Axis (AVG) | 0 | -0.0001 | 1.000 |
| StressZ , Bottom Axis (AVG) | 0.1898 | 0.1898 | 1.000 |
| SOLID186 | |||
| StressZ , Top (AVG) | -0.1898 | -0.1899 | 1.001 |
| StressZ , Neutral Axis (AVG) | 0 | -0.0001 | 1.000 |
| StressZ , Bottom Axis (AVG) | 0.1898 | 0.1898 | 1.000 |