The following examples are available:
The following example is a 2D static magnetic analysis of a solenoid actuator.
The example analysis, based on a solenoid actuator, analyzes the actuator as a 2D axisymmetric model. The example calculates the force on the armature (the moving component of the actuator) and the inductance of the coil. Figure 2.7: Diagram of a Solenoid Actuator below shows you the solenoid actuator:
The analysis uses the parameters listed below to model the actuator geometry:
| Parameter | Description |
|---|---|
| Number of turns in the coil; used in postprocessing | |
| I=1.0 | Current per turn |
| ta=.75 | Thickness of inner leg of magnetic circuit |
| tb=.75 | Thickness of lower leg of magnetic circuit |
| tc=.50 | Thickness of outer leg of magnetic circuit |
| td=.75 | Armature thickness |
| wc=1 | Width of coil |
| hc=2 | Height of coil |
| gap=.25 | Gap |
| space=.25 | Space around coil |
| ws=wc+2*space | |
| hs=hc+.75 | |
| w=ta+ws+tc | Total width of model |
| hb=tb+hs | |
| h=hb+gap+td | Total height of model |
| acoil=wc*hc | Coil area |
| jdens=n*i/acoil | Current density of coil |
The magnetic flux that the coil current produces is assumed to be small enough that no saturation of the iron occurs. This allows a single iteration linear analysis. To simplify the example model, the flux leakage out of the iron at the perimeter of the model is assumed to be minimal. Under normal conditions, the model would include air surrounding the iron to model the effects of flux leakage.
Because no leakage is assumed at the perimeter of the model, the flux flows parallel to the surface. You enforce this by placing a "flux parallel" condition around the model.
For a static (DC) current, you may enter the current in the form of current density over the area of the coil. The APDL is used to compute the current density from the number of turns, the current per turn, and the coil area. The armature is flagged for a force calculation.
In postprocessing, the forces are summarized for the armature, using both a Maxwell stress tensor and a virtual work calculation. Flux density also is displayed. The final postprocessing operation computes the terminal parameters including coil inductance.
Note: The example analysis is only one of many possible 2D static magnetic analyses. Not all such analyses follow exactly the same steps or perform those steps in the same sequence. The properties of the material or materials being analyzed and the conditions surrounding those materials determine which steps a specific analysis needs to include.
For a detailed step-by-step procedure for the magnetic analysis of a solenoid actuator, see the Electromagnetics Tutorial on the Ansys customer site.
You can perform the example static analysis of a solenoid actuator using the commands shown below rather than via the GUI method. All text prefaced by an exclamation point (!) is a comment.
/PREP7 /TITLE, 2D Solenoid Actuator Static Analysis ET,1,PLANE233 ! Define PLANE233 as element type KEYOPT,1,3,1 ! Use axisymmetric analysis option KEYOPT,1,7,1 ! Condense forces at the corner nodes MP,MURX,1,1 ! Define material properties (permeability) MP,MURX,2,1000 ! Permeability of backiron MP,MURX,3,1 ! Permeability of coil MP,MURX,4,2000 ! Permeability of armature /com, ! Set parameter values for analysis n=650 ! Number of coil turns i=1.0 ! Current per turn ta=.75 ! Model dimensions (centimeters) tb=.75 tc=.50 td=.75 wc=1 hc=2 gap=.25 space=.25 ws=wc+2*space hs=hc+.75 w=ta+ws+tc hb=tb+hs h=hb+gap+td acoil=wc*hc ! Cross-section area of coil (cm**2) jdens=n*i/acoil ! Current density (A/cm**2) /PNUM,AREA,1 RECTNG,0,w,0,tb ! Create rectangular areas RECTNG,0,w,tb,hb RECTNG,ta,ta+ws,0,h RECTNG,ta+space,ta+space+wc,tb+space,tb+space+hc AOVLAP,ALL RECTNG,0,w,0,hb+gap RECTNG,0,w,0,h AOVLAP,ALL NUMCMP,AREA ! Compress out unused area numbers APLOT ASEL,S,AREA,,2 ! Assign attributes to coil AATT,3,1,1,0 ASEL,S,AREA,,1 ! Assign attributes to armature ASEL,A,AREA,,12,13 AATT,4,1,1 ASEL,S,AREA,,3,5 ! Assign attributes to backiron ASEL,A,AREA,,7,8 AATT,2,1,1,0 /PNUM,MAT,1 ! Turn material numbers on ALLSEL,ALL APLOT ! Plot areas SMRTSIZE,4 ! Set smart size meshing level 4 (fine) AMESH,ALL ! Mesh all areas ESEL,S,MAT,,4 ! Select armature elements CM,ARM,ELEM ! Define armature as a component ALLSEL,ALL ARSCAL,ALL,,,.01,.01,1,,,1 ! Scale model to MKS (meters) FINISH /SOLU ESEL,S,MAT,,3 ! Select coil elements BFE,ALL,JS,1,,,jdens/.01**2 ! Apply current density (A/m**2) ESEL,ALL NSEL,EXT ! Select exterior nodes D,ALL,AZ,0 ! Set potentials to zero (flux-parallel) ALLSEL,ALL SOLVE FINISH /POST1 PLF2D ! Plot flux lines in the model CMSEL,S,'ARM' NSLE ! Select nodes attached to the armature ESLN ! Select elements attached to the selected nodes EMFT ! Summarize magnetic forces ALLSEL,ALL PLVECT,B,,,,VECT,ELEM,ON ! Plot flux density as vectors /GRAPHICS,POWER ! Turn PowerGraphics on AVRES,2 ! Don't average results across materials PLNSOL,B,SUM ! Plot flux density magnitude FINISH
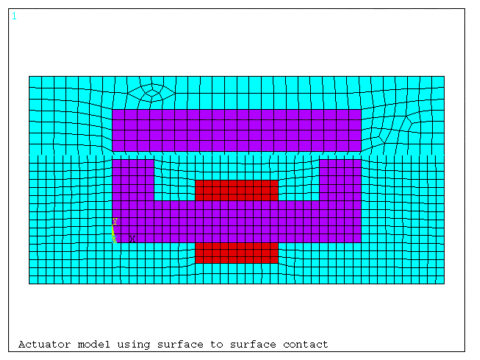
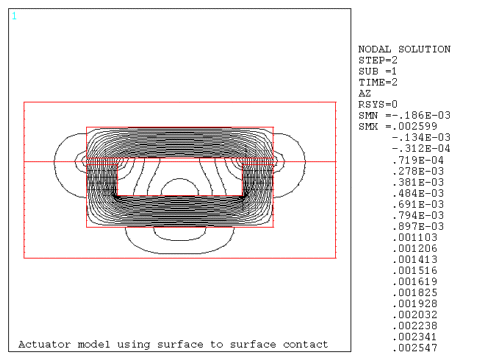
This example presents a 2D model of a coil actuator that demonstrates the use of surface-to-surface contact. Contact is typically used when multiple runs are required with re-positioning of a pole piece in a static or transient analysis, or for convenience in meshing regions with non-connecting meshes.
The contact region is located at the mid-span of the air gap. Two independent meshes are created; one for the lower portion of the model consisting of the back iron, coil, and lower air, and the upper portion consisting of the pole and the upper air. Target elements (TARGE169) are created using the ESURF command on the upper air elements at the air gap (coarser mesh). Contact elements (CONTA172) are created using the ESURF command on the lower air elements at the air gap (finer mesh). The MPC option is selected using bonded contact.
/prep7 /title, Actuator model using surface to surface contact et,1,233 ! plane233 et,2,169 ! Target et,3,172,7,2,,2 ! Contact, MPC option keyopt,3,12,5 ! Bonded contact mp,murx,1,1 tb,bh,2,,40 ! BH curve tbpt,,355,.7 ,,405,.8 ,,470,.9 ,,555,1. ,,673,1.1 ,,836,1.2 ,,1065,1.3 ,,1220,1.35 ,,1420,1.4 ,,1720,1.45 ,,2130,1.5 ,,2670,1.55 ,,3480,1.6 ,,4500,1.65 ,,5950,1.70 ,,7650,1.75 ,,10100,1.8 ,,13000,1.85 ,,15900,1.9 ,,21100,1.95 ,,26300,2. ,,32900,2.05 ,,42700,2.1 ,,61700,2.15 ,,84300,2.2 ,,110000,2.25 ,,135000,2.3 ,,200000,2.41 ,,400000,2.69 ,,800000,3.22 mp,murx,3,1 ! coil ! create backiron rectng,0,.06,0,.01 rectng,0,.01,.01,.02 rectng,.05,.06,.01,.02 ! create coil rectng,.02,.04,-.005,0 rectng,.02,.04,.01,.015 aglue,all ! create lower air domain rectng,-.02,.08,-.01,.021 aovlap,all numcmp,area cm,lower,area ! create pole rectng,0,.06,.022,.032 ! create upper air rectng,-.02,.08,.021,.04 aovlap,7,8 asel,s,area,,7,9 cm,upper,area asel,s,area,,4,6 aatt,2,1,1 ! backiron asel,s,area,,7 aatt,2,1,1 ! pole asel,s,area,,2,3 aatt,3,1,1 ! coil cmsel,s,lower esize,.002 amesh,all cmsel,s,upper esize,.003 amesh,all esla,s nsle,s nsel,r,loc,y,.021 real,2 ! target element needs a real constant ID type,2 esurf ! mesh target elements cmsel,s,lower esla,s nsle,s nsel,r,loc,y,.021 type,3 esurf ! mesh contact elements allsel,all nsel,s,loc,x,-.02 nsel,a,loc,x,.08 nsel,a,loc,y,-.01 nsel,a,loc,y,.04 d,all,az,0 ! flux parallel asel,s,area,,3 esla,s bfe,all,js,,,,5e6 ! coil current density asel,s,area,,2 esla,s bfe,all,js,,,,-5e6 allsel,all finish /solu solve finish /post1 plf2d plnsol,b,sum fini
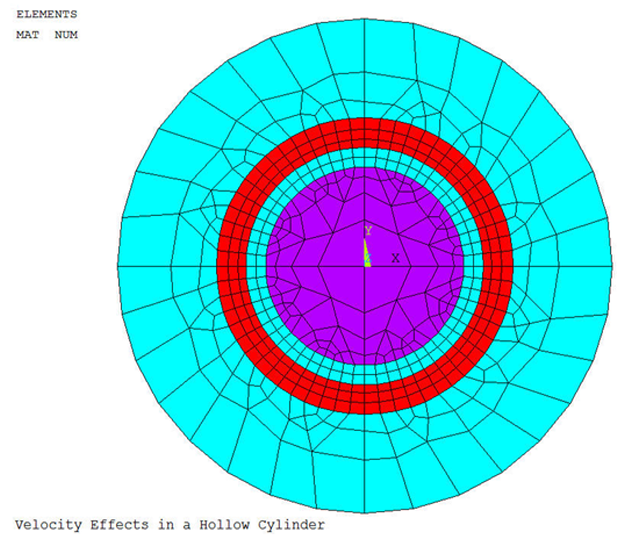
This example demonstrates the use of the velocity effects in a 2D model of a hollow conductive cylinder rotating around a stationary permanent magnet.
A long conductive hollow cylinder rotates about its axis. A stationary solid cylindrical permanent magnet resides with the hollow rotating one. The two bodies are concentric, and the permanent magnet is poled in a direction normal to its axis. The ends of the rotating hollow cylinder are electrically insulated, so the net current flowing in the axial direction is zero (open terminal conductor).
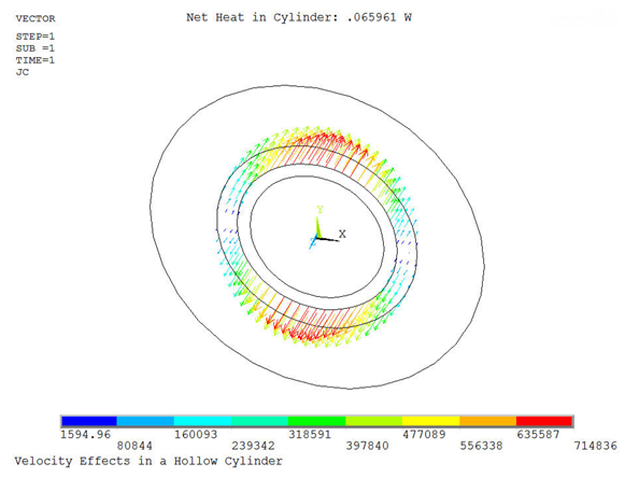
The objective is to determine the Joule heat per unit length in the rotating conductive cylinder and display the eddy currents induced in it by the velocity effects. The evaluation is made half-way along the length of the rotating cylinder, well away from insulated ends where the induced current will reverse direction and have significant non-axial components.
/title, Velocity Effects in a Hollow Cylinder /nopr /pnu,mat,1 /num,1 C********************************************************* C*** PARAMETERS C********************************************************* pi=acos(-1) r_PM=0.010 r1_cyl=0.012 r2_cyl=0.015 r_dmn=0.025 l=0.050 Hc_PM=1e6 mur_PM=1.04 rsv_cyl=3e-8 mur_cyl=1 omga=50 ! ANGULAR VELOCITY, RPM C********************************************************* C*** GEOMETRY C********************************************************* /prep7 asel,none pcir,r_PM,,0,90 aatt,2,2,2 asel,none pcirc,r1_cyl,r2_cyl,0,90 aatt,3,3,3 alls cm,keep_a,area asel,none pcirc,r_dmn,,0,90 cm,scrap_a,area alls asba,scrap_a,keep_a,,dele,keep cmse,u,keep_a aatt,1,1,1 alls aplo C********************************************************* C*** ATTRIBUTES, MESH C********************************************************* et,1,233 mp,murx,1,1 et,2,233 mp,murx,2,mur_PM mp,mgyy,2,Hc_PM et,3,233,1 ! CYLINDER mp,murx,3,mur_cyl mp,rsvx,3,rsv_cyl alls ames,all csys,1 agen,4,all,,,0,90,0 numm,node,1e-8,1e-8 numm,kp,1e-8,1e-8 C********************************************************* C*** BCs C********************************************************* alls nsel,s,ext d,all,az esel,s,mat,,3 nsle cp,1,volt,all alls C********************************************************* C*** LOAD C********************************************************* bf,all,velo,,,,,,omga*(2*pi)/60 ! Angular velocity, rad/sec C********************************************************* C*** SOLVE C********************************************************* /solu solve fini C********************************************************* C*** RESULTS C********************************************************* /post1 set etab,,jhea etab,,volu smul,ht,jhea,volu ssum *get,ht_total,ssum,,item,ht ht_total=ht_total*l /ann,dele /tla,-0.25,0.90, Net Heat in Cylinder: %ht_total% W /vie,1,1,2,3 plve,jc,,,,vect,,on /com, /com, Net Heat in Cylinder: %ht_total% W /com, fini
Another Ansys, Inc., publication, the Mechanical APDL Verification Manual, contains several additional examples of 2D static magnetic analyses: