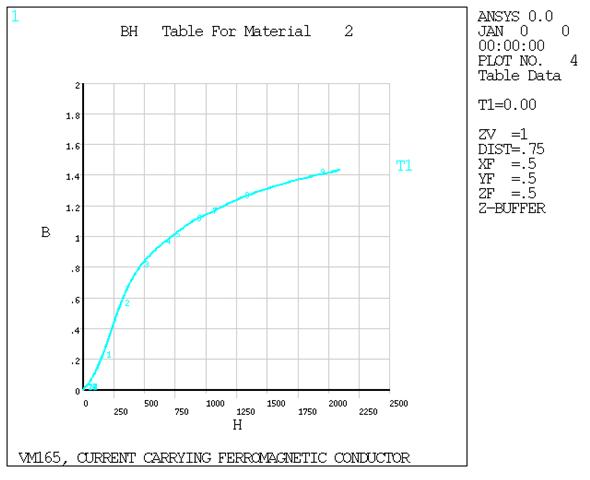
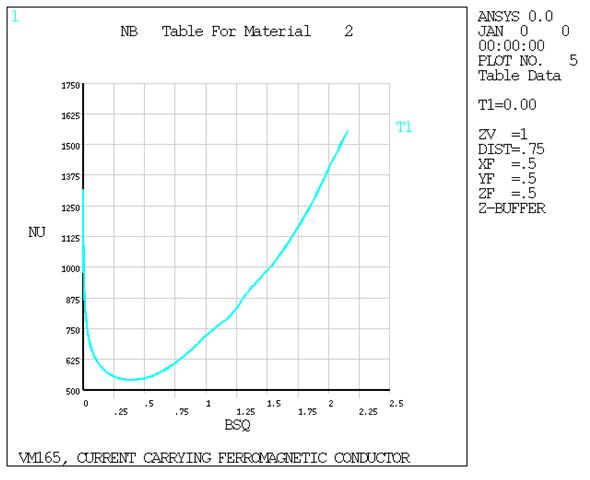
VM165

VM165
Current-Carrying Ferromagnetic Conductor

Overview

Reference:

W. B. Boast, Principles of Electric and Magnetic Fields, Harper & Brothers, New York, NY, 1948, pg. 225.

Analysis Type(s):

Nonlinear Static Magnetics Analysis (ANTYPE = 0)

Element Type(s):

2D 8-Node Electromagnetic Elements (PLANE233)

2D Infinite Solid Elements (INFIN110)

Input Listing:

vm165.dat

Test Case

A long cylindrical shell of cast steel carries a constant current I uniformly distributed within the conductor cross-section. Determine the tangential magnetic flux density B_θ at several locations within the conductor.

Figure 232: Current-Carrying Ferromagnetic Conductor Problem Sketch

Material Properties

Geometric Properties

B-H curve as shown in Table 2: B-H Data

Inner radius of the ring, r_i = 0.3 in

Outer radius of the ring, r_o = 0.45 in

Outer radius of the external air, r₁ = 0.75 in

I = 100 A

Table 2: B-H Data

B(T)[1]	0.21	0.55	0.80	0.95	1.0	1.1	1.15	1.25	1.40
H(A/m)[1]	150	300	460	640	720	890	1020	1280	1900

Graphical estimate from reference.

Analysis Assumptions and Modeling Notes

The conductor is assumed to be infinitely long, thus end effects can be ignored allowing for a two-dimensional planar analysis. Since the field is symmetric around the circumference, only a single, one-element width slice is chosen for modeling. The circumferential width of the slice is chosen as 5° to produce reasonable element aspect ratios. The external air is modeled to a radius of 0.75 inches. Infinite solid elements are used from there to a radius of 1.5 inches to model the far-field decay.

The MKS system of units is used for the analysis. The conversion factor, 0.0254, used in the KPSCALE command, converts the geometry input units from inches to meters. The current density is calculated as = 2.28019 x 10^-4 A/in² = 438559 A/m².

Results Comparison

	Target	Mechanical APDL	Ratio
Bangle, T @ r = .325 in	0.48	0.48	1.010
Bangle, T @ r = .375 in	1.03	1.03	0.996
Bangle, T @ r = .425 in	1.22	1.22	0.996

Figure 233: B-H Curve using PLANE233 elements

Figure 234: NU-B² Curve using PLANE233 elements