This section introduces the harmonic cyclic symmetry analysis capability with an example problem. The example presents a simplified ring-strut-ring structure used in many rotating-machinery applications.
The component is a simplified fan inlet case for a military aircraft engine. As part of the design process for the assembly, the harmonic response characteristics of the inlet case may be investigated, as shown in this example.
The geometric and material properties used for the harmonic cyclic analysis are the same as used in Example Modal Cyclic Symmetry Analysis.
All applicable degrees of freedom are used for the cyclic symmetry edge-component pairs. The harmonic response to a pressure load applied on the assembly is computed.
Use the input file given below (named harm_cyc_symm.inp) to perform the example harmonic cyclic symmetry analysis. The file contains the complete geometry, material properties and solution options for the finite element model.
! Harmonic Cyclic Symmetry Analysis Example ! Ring-Strut-Ring Configuration ! STEP #1 ! Start an interactive session ! STEP #2 ! Read in this input file: harm_cyc_symm.inp finish /clear r1=5 r2=10 d1=2 nsect=24 alpha_deg=360/nsect alpha_rad=2*acos(-1)/nsect /view,1,1,1,2 /plopts,minm,0 /plopts,date,0 /pnum,real,1 /number,1 /prep7 csys,1 k,1,0,0,0 k,2,0,0,d1 k,3,r1,0,0 k,4,r1,0,d1 l,3,4 arotat,1,,,,,,1,2,alpha_deg/2 k,7,r2,0,0 k,8,r2,0,d1 l,7,8 arotat,5,,,,,,1,2,alpha_deg/2 arotat,2,,,,,,1,2,alpha_deg/2 arotat,6,,,,,,1,2,alpha_deg/2 a,5,6,10,9 mshkey,1 et,1,181 r,1,0.20 r,2,0.1 mp,ex,1,10e6 mp,prxy,1,0.3 mp,dens,1,1e-4 esize,0.5 asel,,,,1,4 aatt,,1 asel,,,,5 aatt,,2 allsel dk,5,all,0 aplot /prep7 !/eof ! STEP #3 ! Configure the database for a cyclic symmetry analysis cyclic ! STEP #4 ! Mesh the areas amesh,all ! STEP #5 ! Turn on cyclic symmetry graphical expansion /cycexpand,,on ! STEP #6 ! Plot the elements eplot ! STEP #7 ! List the cyclic status cyclic,status ! STEP #8 ! List the cyclic solution option settings cycopt,status fini ! STEP #9 ! Solve the harmonic cyclic symmetry analysis /solution ! Specify harmonic analysis option and frequency sweep values antype,harmic hropt,full harfrq,860,878 nsub,9 ! Apply pressure load on the outer surface area asel,s,area,,2 asel,a,area,,4 ! Loading to be applied on sector number 3 cycopt,ldsect,3 sfa,all,,pres,-124 asel,all solve fini ! STEP #10 ! Go to database results post processor /post1 set,list ! STEP #11 ! Read results for "substep 3 - excitation freq. of 866 HZ" set,,3 plns,u,sum,1 fini ! STEP #12 ! Go to time/freq. history postprocessor /post26 ! STEP #13 ! Store X and Y disp. of node #34 on sector #3" nsol,2,34,U,x,UX_34,3 nsol,3,34,U,y,UY_34,3 ! STEP #14 ! Plot UX and UY disp. of node #34 as a function of freq. plvar,2,3
The following table describes the input listing and the steps involved in the example harmonic cyclic symmetry analysis in detail.
| Step | Step Description | Description |
| 1. | Start an interactive session. | --- |
| 2. | Read the input file: harm_cyc_symm.inp. | /INPUT,HARM,CYC_SYMM.INP |
| 3. | Specify a cyclic symmetry analysis and configure the database accordingly. | CYCLIC |
| 4. | Mesh the areas. | AMESH,ALL |
| 5. | Activate cyclic symmetry graphical expansion. | /CYCEXPAND,,ON |
| 6. | Plot the elements. Figure 5.5: Element Plot Showing Pressure Load on Sector 3 shows an element plot showing pressure load on sector 3. | EPLOT |
| 7. | List the cyclic status. | CYCLIC,STATUS |
| 8. | List the cyclic solution option settings. | CYCOPT,STATUS |
| 9. | Solve the harmonic cyclic symmetry analysis with non-cyclic loading. |
CYCOPT,LDSECT |
| 10. | Enter database results postprocessor. | /POST1 |
| 11. | Read results for sub step 3 – Frequency = 866. | SET,1,3 |
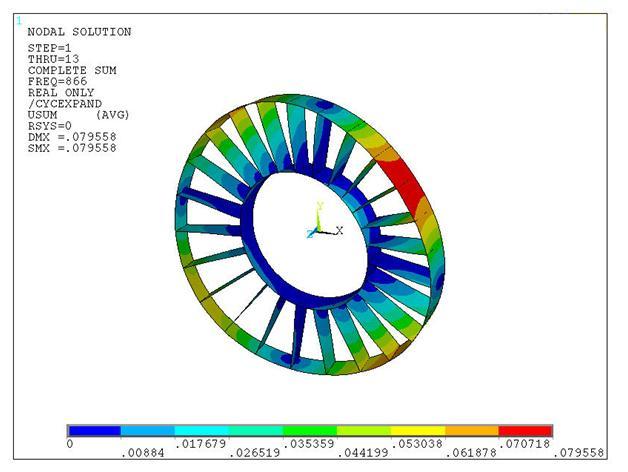
| 12. | Plot the displacement sum contour. Figure 5.6: Contour Plot of Displacement Sum at Frequency of 866 HZ shows a contour plot of displacement sum at frequency = 866 HZ. | PLNSOL,U,SUM |
| 13. | Enter time/frequency history postprocessor. | /POST26 |
| 14. | Store nodal data from results file for node 34, sector 3. | NSOL,2,34,u,x,UX_34,3 |
| NSOL,3,34,u,y,UY_34,3 | ||
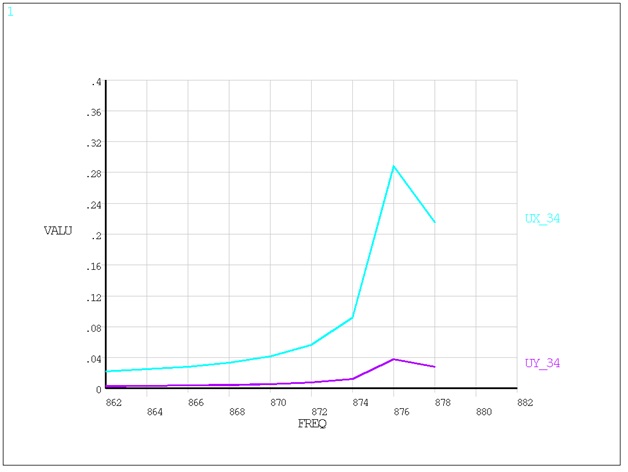
| 15. | Plot frequency versus displacement. Plot at node 34. Figure 5.7: Displacement Plot as a Function of Excitation Frequency shows the displacement plot as a function of the excitation frequency. | PLVAR,2,3 |
The results of your analysis should match those shown below: