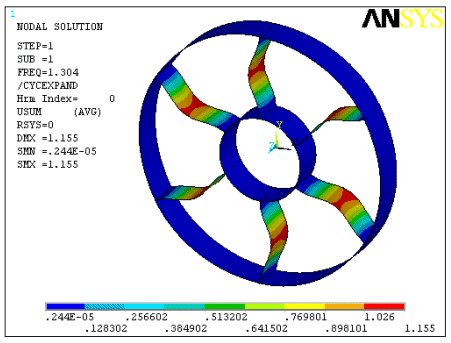
This example buckling cyclic symmetry analysis presents a simplified ring-strut-ring structure used in many rotating-machinery applications.
The object is a simplified structure that experiences a thermal load emanating outward from the center. The inner ring is kept at a constant 600° F temperature and the outer ring is kept at a constant 0° F. A linear eigenvalue buckling analysis determines when the struts will buckle as the temperature in the struts increases from 100° F to 500° F.
The geometric properties for this analysis are as follows:
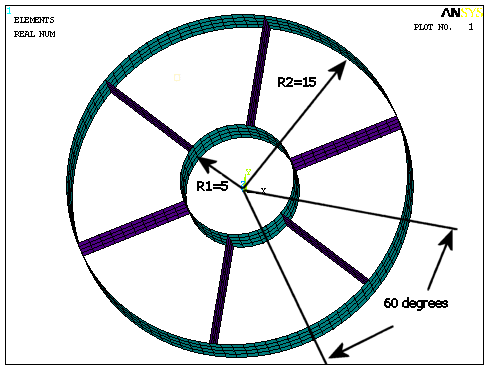
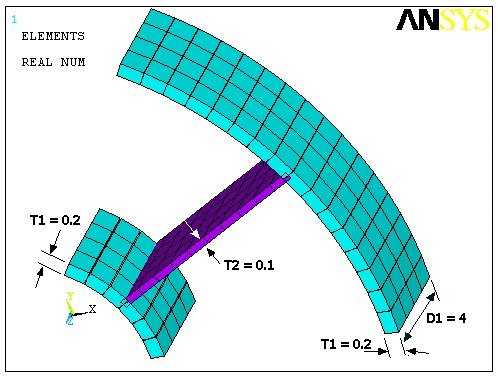
The material properties for this analysis are as follows:
| Poisson's ratio (υ) = 0.3 |
| Density = 1e-4 |
| Coefficient of thermal expansion (α) = 5e-5 |
| Young's modulus (E) = 10e6 (at 0° F) |
| Young's modulus (E) = 4e6 (at 600° F) |
The Young's modulus value varies linearly between 0 and 600° F. All applicable degrees of freedom (DOFs) are used for the cyclic symmetry edge-component pairs. The first six mode shapes for all applicable harmonic indices are requested.
Use this input file (named buck_cyc_sym.inp) to perform the buckling cyclic symmetry analysis example. The file contains the complete geometry, material properties and solution options for the finite element model.
! Cyclic Symmetry Buckling Example ! Ring-Strut-Ring Configuration ! STEP #1 ! Start an interactive session ! STEP #2 ! Read in the input file: buck_cyc_sym.inp r1=5 r2=15 d1=4 nsect=6 alpha_deg=360/nsect alpha_rad=2*acos(-1)/nsect /view,1,1,1,2 /plopts,minm,0 /plopts,date,0 /pnum,real,1 /number,1 /prep7 csys,1 k,1,0,0,0 k,2,0,0,d1 k,3,r1,0,0 k,4,r1,0,d1 l,3,4 arotat,1,,,,,,1,2,alpha_deg/2 k,7,r2,0,0 k,8,r2,0,d1 l,7,8 arotat,5,,,,,,1,2,alpha_deg/2 arotat,2,,,,,,1,2,alpha_deg/2 arotat,6,,,,,,1,2,alpha_deg/2 a,5,6,10,9 mshkey,1 et,1,181 r,1,0.20 r,2,0.1 mptemp,1,0 mptemp,2,600 mpdata,ex,1,1,10e6 mpdata,ex,1,2,4e6 mp,prxy,1,0.3,0.0 mp,dens,1,1e-4 mp,alpx,1,5e-5 tref,0 esize,1.0 asel,,loc,x,r1 bfa,all,temp,600 asel,a,loc,x,r2 aatt,,1 asel,inve bfa,all,temp,100 aatt,,2 allsel amesh,all lsel,,loc,z,d1/2 lsel,r,loc,y,alpha_deg/2 ksll nslk nrotate,all dk,all,uz,0 dk,all,uy,0 allsel finish aplot /prep7 /eof ! STEP #3 ! Configure the database for a cyclic symmetry analysis cyclic ! STEP #4 ! Turn on cyclic symmetry graphical expansion /cycexpand,,on ! STEP #5 ! Plot the elements eplot ! STEP #6 ! List the cyclic status cyclic,status ! STEP #7 ! List the cyclic solution option settings cycopt,status ! STEP #8 ! Specify static analysis type with prestress effects /solution antype,static pstres,on ! STEP #9 ! Solve the prestress static analysis solve ! STEP #10 ! Specify buckling analysis type finish /solution antype,buckle ! STEP #11 ! Specify buckling analysis options bucopt,lanb,3 ! STEP #12 ! Specify mode expansion options mxpand,3,,,yes ! STEP #13 ! Solve the buckling analysis solve ! STEP #14 ! Read results for the smallest load factor finish /post1 set,first,,,,,,,order ! STEP #15 ! Plot the buckled mode shape plnsol,u,sum
The following table describes the input listing and the steps involved in the example buckling cyclic symmetry analysis in more detail.
| Step | Description | Command |
|---|---|---|
| 1. |
Start an interactive session. |
--- |
| 2. |
Read in the input file: buck_cyc_sym.inp | /INPUT,buck_cyc_sym.inp |
| 3. |
Specify a cyclic symmetry analysis and configure the database accordingly. | CYCLIC |
| 4. |
Activate cyclic symmetry graphical expansion. | /CYCEXPAND,,ON |
| 5. |
Plot the elements. | EPLOT |
| 6. |
List the cyclic status. | CYCLIC,STATUS |
| 7. |
List the cyclic solution option settings. | CYCOPT,STATUS |
| 8. |
Specify a static analysis type with prestress effects. | |
| 9. |
Solve the prestress static analysis. | |
| 10. |
Specify a buckling analysis type. | |
| 11. |
Specify buckling analysis options | BUCOPT, LANB, 3 |
| 12. |
Specify mode expansion options. | MXPAND, 3, , , YES |
| 13. | Solve the buckling analysis. | SOLVE |
| 14. | Read the results from the smallest load factor. (This should correspond to the smallest frequency.) | |
| 15. |
Plot the buckled mode shape. ---- This step completes the example buckling cyclic symmetry analysis. Your results should match those shown in Figure 5.2: Example Buckling Cyclic Symmetry Analysis Results. | PLNSOL, U, SUM |
The results of your analysis should match those shown here:
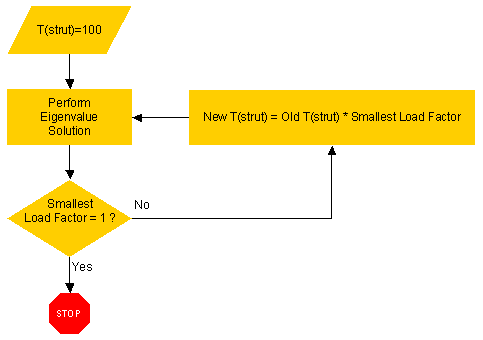
You can automatically solve for the critical strut temperature by iterating on the variable loads until the eigenvalue becomes 1.0 (or nearly 1.0 within some tolerance). The iterations ensure that the eigenvalue solution does not factor the stress stiffness matrix from the constant loads. The following flowchart illustrates the process:
Use the /PREP7 portion of the previous input file (buck_cyc_sym.inp) to construct your model. After defining the model parameters--but before activating cyclic symmetry--define the arrays and the programming operations, as follows:
*dim,Tstrut,array,10
*dim,Tfact,array,10
*do,I,1,10
/prep7
*if,I,eq,1,then
Tstrut(I)=100
*else
Tstrut(I)=Tstrut(I-1)*Tfact(I-1)
cyclic,undouble
*endif
asel,,real,,2
bfa,all,temp,Tstrut(I)
allsel
After you have defined the iterative parameters, proceed with the cyclic symmetry portion of the analysis:
cyclic /cycexpand,,on eplot cyclic,status cycopt,status /solution antype,static pstres,on solve finish /solution antype,buckle bucopt,lanb,3 mxpand,3,,,yes solve finish /post1 set,first,,,,,,,order plnsol,u,sum *get,loadmult,active,,set,freq Tfact(I)=loadmult *enddo
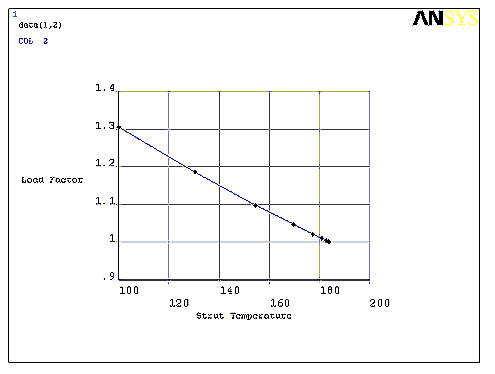
The program then plots the data to determine the critical strut temperature:
*dim,data,table,10,2 data(0,1)=1 data(0,2)=2 *do,I,1,10 data(I,0)=I data(I,1)=Tstrut(I) data(I,2)=Tfact(I) *enddo /AXLAB,X,Strut Temperature /AXLAB,Y,Load Factor /GROPT,DIVX,5 /GROPT,DIVY,5 /XRANGE,100,200 /YRANGE,0.9,1.4 /GTHK,CURVE,1 /GMARKER,1,3 *VPLOT,data(1,1),data(1,2)
The eigenvalues (frequencies) calculated for the buckling analysis represent the buckling load factors. The eigenvalues represent load factors for all applied loads.
The iteration strategy yields the following results:
Table 5.1: Buckling Cyclic Symmetry: Load Factor Iteration Results
| Iteration | T° (Strut) | Load Factor |
|---|---|---|
| 1 | 100.00 | 1.3039 |
| 2 | 130.39 | 1.1845 |
| 3 | 154.44 | 1.0972 |
| 4 | 169.45 | 1.0461 |
| 5 | 177.27 | 1.0206 |
| 6 | 180.91 | 1.0089 |
| 7 | 182.52 | 1.0038 |
| 8 | 183.21 | 1.0016 |
| 9 | 183.50 | 1.0007 |
| 10 | 183.62 | 1.0003 |
A graph of the results shows the convergence at Load Factor = 1.0: