VM-WB-MECH-087

VM-WB-MECH-087
Campbell Diagrams and Critical Speeds Using Symmetric Orthotropic Bearings

Overview

Reference:

Nelson, H.D., & McVaugh, J.M. (1976). The Dynamics of Rotor-Bearing Systems Using Finite Elements. Journal of Engineering for Industry, 98(4), 593-600.

Solver(s):

Ansys Mechanical

Analysis Type(s):

Modal Analysis

Element Type(s):

Line Body

Point Mass

Bearing Connection

Test Case

A rotor-bearing system is analyzed to determine the forward and backward whirl speeds. The distributed rotor is modeled as a configuration of six elements, with each element composed of subelements. See Table 1: Geometric Data of Rotor-Bearing Elements for a list of the geometric data of the individual elements. Two symmetric orthotropic bearings are located at positions four and six. A modal analysis is performed on the rotor-bearing system with multiple load steps to determine the whirl speeds and Campbell values for the system.

This problem is also presented in

VM254

in the Mechanical APDL Verification Manual.

Figure 116: Rotor-Bearing Configuration

Table 1: Geometric Data of Rotor-Bearing Elements

Element Number	Subelement number	Axial Distance to Subelement	Inner Diameter (cm)	Outer Diameter (cm)
1	1	0.00		1.02
1	2	1.27		2.04
2	1	5.08		1.52
2	2	7.62		4.06
3	1	8.89		4.06
	2	10.16		6.60
	3	10.67	1.52	6.60
	4	11.43	1.78	5.08
	5	12.70		5.08
	6	13.46		2.54
4	1	16.51		2.54
4	2	19.05		3.04
5	1	22.86		3.04
5	2	26.67		2.54
6	1	28.70		2.54
	2	30.48		7.62
	3	31.50		4.06
	4	34.54	1.52	4.06

Material Properties

Geometric Properties

Shaft

E₁₁ = 2.078 x 10¹¹ Pa

G₁₂ = 1.0 x 10¹⁴ Pa

Density = 7806 kg/m³

Mass Element

Mass = 1.401 kg

Polar inertia = 0.002 kg⋅m²

Diametral inertia = 0.00136 kg⋅m²

Bearing Element

Spring coefficients

K11 = K22 = 3.503 x 10⁷ N/m

K12 = K21 = -8.756 x 10⁶ N/m

Refer to Table 1: Geometric Data of Rotor-Bearing Elements

Rotational Velocity

Spin (1) = 1000 RPM

Spin (2) = 20000 RPM

Spin (3) = 40000 RPM

Spin (4) = 60000 RPM

Spin (5) = 80000 RPM

Spin (6) = 100000 RPM

Analysis Assumptions and Modeling Notes

A modal analysis is performed on the rotor-bearing system with QR Damp methods using pipe elements (PIPE288) to determine the whirl speeds and Campbell values.

A point mass is used to model the rigid disk (concentrated mass). Two symmetric orthotropic bearings are used to assemble the rotor system. No shear effect is included in the rotor-bearing system. The displacement and rotation along and around the X-axis is constrained so that the rotor-bearing system does not have any torsion or traction related displacements.

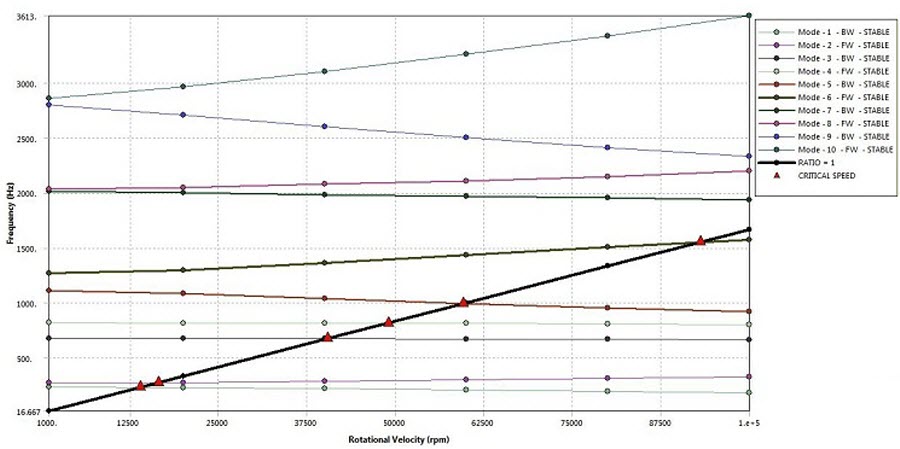
Backward and forward whirl speeds for slope = 1 @ 100000 RPM are determined from the modal analysis.

Results Comparison

	Target	Mechanical	Error (%)
Backward and forward whirl speeds for slope = 1 @ 100000 RPM RPM = Hz * 60
PIPE288
Mode 1 (BW)	10747	10757.4	0.9677
Mode 2 (FW)	19665	19518	-0.7475
Mode 3 (BW)	39077	39656.4	1.4827
Mode 4 (FW)	47549	48196.2	1.3611

Figure 117: Campbell Diagram for Rotor-Bearing System