VM-WB-MECH-088

VM-WB-MECH-088
Harmonic Response of a Guitar String

Overview

Reference:	Blevins, R.D. (1979). Formulas for Natural Frequency and Mode Shape (p. 90, tab. 7-1). New York, NY: Nostrand Reinhold Co.
Solver(s):	Ansys Mechanical
Analysis Type(s):	Static Structural Linear Perturbed Modal Linear Perturbed Harmonic
Element Type(s):	Beam

Test Case

A uniform stainless steel guitar string of length l and diameter d is stretched between two rigid supports by a tensioning force F₁, which is required to tune the string to the E note of a C scale. The string is then struck near the quarter point with a force F₂. Determine the fundamental frequency, f₁. Also, show that only the odd-numbered frequencies produce a response at the midpoint of the string for this excitation.

This problem is also presented in

VM76

in the Mechanical APDL Verification Manual.

Material Properties

Geometric Properties

E = 190 x 10⁹ Pa

ρ = 7920 kg/m³

l = 710 mm

c = 165 mm

d = 0.254 mm

F₁ = 84 N

F₂ = 1 N

Analysis Assumptions and Modeling Notes

Enough elements are selected so that the model can be used to adequately characterize the string dynamics. The stress stiffening capability of the elements is used. Linear perturbed harmonic analysis determines the displacement response to the lateral force F₂.

Figure 118: Guitar String Problem

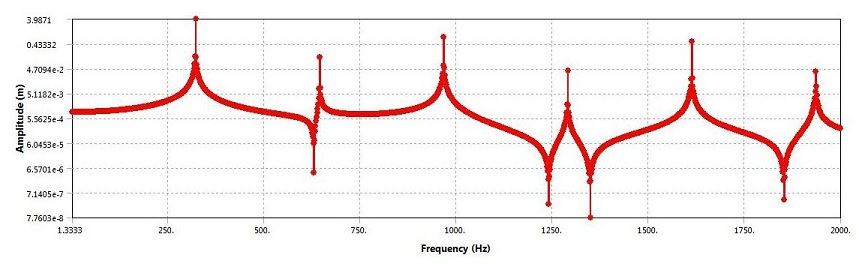
Results Comparison

		Target	Mechanical	Error (%)
Modal	f, Hz	322.2	322.67	0.15
Frequency Response	f₁, (322.2 Hz)	Response	Response, 320 < f < 328	-
	f₂, (644.4 Hz)	No Response	No Response	-
	f₃, (966.6 Hz)	Response	Response, 966 < f < 974	-
	f₄, (1288.8 Hz)	No Response	No Response	-
	f₅, (1611.0 Hz)	Response	Response, 1611 < f < 1619	-
	f₆, (1933.2 Hz)	No Response	No Response	-

Figure 119: String Midpoint Displacement Amplitude