Two significant advantages of the unstructured mesh capability in Ansys Fluent are:
reduced setup time compared to structured meshes
the ability to incorporate solution-adaptive refinement of the mesh
By using solution-adaptive refinement, you can add cells where they are needed in the mesh, thus enabling the features of the flow field to be better resolved. When adaption is used properly, the resulting mesh is optimal for the flow solution because the solution is used to determine where more cells need to be added. Thus, computational resources are not wasted by the inclusion of unnecessary cells, as occurs in the structured mesh approach. Also, the effect of mesh refinement on the solution can be studied without completely regenerating the mesh.
Note: When you are running in parallel, Fluent performs load balancing, which redistributes cells across compute nodes. Refer to Partitioning the Mesh Automatically and Load Balancing for additional information on load balancing. After the mesh is adapted, Fluent automatically performs a load balancing step, by default.
For more information about the adaption process, see Adaption Process in the Theory Guide.
See the following sections for information on performing mesh adaption:
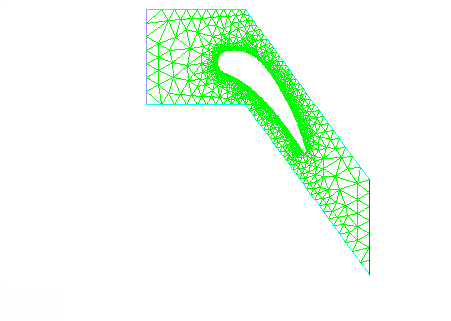
An example of the effective use of adaption is in the solution of the compressible, turbulent flow through a 2D turbine cascade. The initial mesh around the blade is fine, as shown in Figure 38.1: Turbine Cascade Mesh Before Adaption. The surface node distribution thus provides adequate definition of the blade geometry, and enables the turbulent boundary layer to be properly resolved without further adaption. On the other hand, the mesh on the inlet, outlet, and periodic boundaries is comparatively coarse. To ensure that the flow in the blade passage is appropriately resolved, solution-adaptive refinement was used to create the mesh shown in Figure 38.2: Turbine Cascade Mesh after Adaption.
While the procedure for solution adaption will vary according to the flow being solved, it is instructive to examine the adaption process used for the turbine cascade shown in the previous figure. Though this example involves compressible flow, the general procedure is applicable for incompressible flows as well.
Display contours of pressure to determine a suitable refinement threshold.
Mark the cells within the refinement threshold, creating a refinement register (see Field Variable).
Repeat the process described in steps 1 and 2, using gradients of Mach number as a refinement criterion.
To refine in the wake region, use isovalues of total pressure as a criterion (see Field Variable). This causes cells within the boundary layer and the wake to be marked, since these are both regions of high total-pressure loss.
Refine the cells contained in the register (see Refining and Coarsening).
The effect of refining on gradients is evident in the finer mesh ahead of the leading edge of the blade and within the blade passage (Figure 38.2: Turbine Cascade Mesh after Adaption). The finer mesh in the wake region is due to the adaption using isovalues of total pressure.
The advantages of solution-adaptive refinement, when used properly (as in the turbine cascade example in Adaption Example), are significant. However, this capability must be used carefully to avoid certain pitfalls. Some guidelines for proper usage of solution-adaptive refinement are as follows:
The surface mesh must be fine enough to adequately represent the important features of the geometry.
For example, it would be bad practice to place too few nodes on the surface of a highly-curved airfoil, and then use solution refinement to add nodes on the surface. The surface will always contain the facets contained in the initial mesh, regardless of the additional nodes introduced by refinement.
The initial mesh should contain sufficient cells to capture the essential features of the flow field.
Consider the following example, in which you want to predict the shock forming around a bluff body in supersonic flow. To obtain a reasonable first solution, the initial mesh should contain enough cells and also have sufficient resolution to represent the shape of the body. Subsequent gradient adaption can be used to sharpen the shock and to establish a mesh-independent solution.
Polyhedral cells are only eligible for adaption with the default polyhedral unstructured mesh adaption (PUMA) method.
For the hanging node adaption method, the presence of polyhedral cells in a mesh may or may not limit the eligibility of other cells for adaption, depending on the manner in which the polyhedral cells were created:
If the domain was converted to polyhedra (see Converting the Domain to a Polyhedra), then no part of the mesh can be adapted (even if hexahedral cells are present in the mesh after conversion).
If the polyhedra are a result of converting skewed tetrahedral cells (see Converting Skewed Cells to Polyhedra) or converting cells adjacent to hanging nodes / edges (see Converting Cells with Hanging Nodes / Edges to Polyhedra), then the non-polyhedral cells may be adapted. The polyhedral cells, however, will be automatically unmarked from the register when adaption is initiated and will remain unchanged.
Obtain a reasonably well-converged solution before performing an adaption. If you adapt to an incorrect solution, cells will be added in the wrong region of the flow.
Use careful judgment in deciding how well to converge the solution before adapting, because there is a trade-off between adapting too early to an unconverged solution and wasting time by continuing to iterate when the solution is not changing significantly. This does not directly apply to automatic adaption, because here the solution is adapted at regular intervals of iterations or time steps, depending on which solver is being used.
Write a case and data file before starting the adaption process. If you generate an undesirable mesh, you can restart the process with the saved files. This does not directly apply to automatic adaption, because here the solution is adapted at regular intervals of iterations or time steps, depending on which solver is being used.
Select suitable variables when performing gradient adaption. For some flows, the choice is clear. For instance, adapting on gradients of pressure is a good criterion for refining in the region of shock waves. In most incompressible flows, however, it makes little sense to refine on pressure gradients. A more suitable parameter in an incompressible flow might be mean velocity gradients. If the flow feature of interest is a turbulent shear flow, it will be important to resolve the gradients of turbulent kinetic energy and turbulent energy dissipation, so these might be appropriate refinement variables. In reacting flows, temperature or concentration (or mole or mass fraction) of reacting species might be appropriate.
Do not over-refine a particular region of the solution domain. It causes very large gradients in cell volume. Such poor adaption practice can adversely affect the accuracy of the solution.