Plasticity theory provides a mathematical relationship that characterizes the elastoplastic response of materials. There are three ingredients in the rate-independent plasticity theory: the yield criterion, flow rule and the hardening rule. Table 4.1: Notation summarizes the notation used in the remainder of this chapter.

The yield criterion determines the stress level at which yielding is initiated. For multi-component stresses, this is represented as a function of the individual components, , which can be interpreted as an equivalent stress :

(4–4)

where:

= stress vector

Table 4.1: Notation

Variable	Definition	Mechanical APDL Output Label
	elastic strains	EPEL
	plastic strains	EPPL
	trial strain
	equivalent plastic strain	EPEQ
	stresses	S
	equivalent stress
	material yield parameter
	mean or hydrostatic stress	HPRES
	equivalent stress parameter	SEPL
	plastic multiplier
	yield surface translation
	plastic work
	translation multiplier
	stress-strain matrix
	tangent modulus
	yield criterion
	stress ratio	SRAT
	plastic potential
	deviatoric stress

When the equivalent stress is equal to a material yield parameter σ_y,

(4–5)

the material will develop plastic strains. If is less than , the material is elastic and the stresses will develop according to the elastic stress-strain relations. Note that the equivalent stress can never exceed the material yield since in this case plastic strains would develop instantaneously, thereby reducing the stress to the material yield. Equation 4–5 can be plotted in stress space as shown in Figure 4.2: Various Yield Surfaces for some of the plasticity options. The surfaces in Figure 4.2: Various Yield Surfaces are known as the yield surfaces and any stress state inside the surface is elastic, that is, they do not cause plastic strains.

Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options

Figure 4.2: Various Yield Surfaces

The flow rule determines the direction of plastic straining and is given as:

(4–6)

where:

= plastic multiplier (which determines the amount of plastic straining)

= function of stress termed the plastic potential (which determines the direction of plastic straining)

If is the yield function (as is normally assumed), the flow rule is termed associative and the plastic strains occur in a direction normal to the yield surface.

The hardening rule describes the changing of the yield surface with progressive yielding, so that the conditions (stress states) for subsequent yielding can be established. Two hardening rules are available: work (or isotropic) hardening and kinematic hardening. In work hardening, the yield surface remains centered about its initial center line and expands in size as the plastic strains develop. For materials with isotropic plastic behavior this is termed isotropic hardening and is shown in Figure 4.3: Types of Hardening Rules (a). Kinematic hardening assumes that the yield surface remains constant in size and the surface translates in stress space with progressive yielding, as shown in Figure 4.3: Types of Hardening Rules (b).

The yield criterion, flow rule and hardening rule for each option are summarized in Table 4.2: Summary of Plasticity Options and are discussed in detail later in this chapter.

Figure 4.3: Types of Hardening Rules

If the equivalent stress calculated using elastic properties exceeds the material yield, then plastic straining must occur. Plastic strains reduce the stress state so that it satisfies the yield criterion, Equation 4–5. Based on the theory presented in the previous section, the plastic strain increment is readily calculated.

The hardening rule states that the yield criterion changes with work hardening and/or with kinematic hardening. Incorporating these dependencies into Equation 4–5, and recasting it into the following form:

(4–7)

where:

= plastic work

= translation of yield surface

and are termed internal or state variables. Specifically, the plastic work is the sum of the plastic work done over the history of loading:

(4–8)

where:

and translation (or shift) of the yield surface is also history dependent and is given as:

(4–9)

where:

= material parameter

= backstress (location of the center of the yield surface)

Equation 4–7 can be differentiated so that the consistency condition is:

(4–10)

Noting from Equation 4–8 that

(4–11)

and from Equation 4–9 that

(4–12)

Equation 4–10 becomes

(4–13)

The stress increment can be calculated via the elastic stress-strain relations

(4–14)

where:

= stress-strain matrix

with

(4–15)

since the total strain increment can be divided into an elastic and plastic part. Substituting Equation 4–6 into Equation 4–13 and Equation 4–15 and combining Equation 4–13, Equation 4–14, and Equation 4–15 yields

(4–16)

The size of the plastic strain increment is therefore related to the total increment in strain, the current stress state, and the specific forms of the yield and potential surfaces. The plastic strain increment is then calculated using Equation 4–6:

(4–17)

An Euler backward scheme is used to enforce the consistency condition Equation 4–10. This ensures that the updated stress, strains and internal variables are on the yield surface. The algorithm proceeds as follows:

Note that the Euler backward integration scheme in step 4 is the radial return algorithm (Krieg([47])) for the von Mises yield criterion.

The tangent or elastoplastic stress-strain matrix is derived from the local Newton-Raphson iteration scheme used in step 4 above (Simo and Taylor([156])). It is therefore the consistent (or algorithmic) tangent. If the flow rule is nonassociative (), then the tangent is unsymmetric.

These options use the von Mises yield criterion with the associated flow rule and isotropic (work) hardening (accessed via TB,PLASTIC,,,,BISO).

The equivalent stress Equation 4–4 is:

(4–27)

where {s} is the deviatoric stress Equation 4–37. When is equal to the current yield stress the material is assumed to yield. The yield criterion is:

(4–28)

For work hardening, is a function of the amount of plastic work done. For the case of isotropic plasticity assumed here, can be determined directly from the equivalent plastic strain of Equation 4–43 (output as EPEQ) and the uniaxial stress-strain curve as depicted in Figure 4.4: Uniaxial Behavior. is output as the equivalent stress parameter (output as SEPL).

Figure 4.4: Uniaxial Behavior

For Determination

Both the Voce([253]) hardening law, and the nonlinear power hardening law can be used to model nonlinear isotropic hardening. The Voce hardening law for nonlinear isotropic hardening behavior (accessed with TB,NLISO,,,,VOCE) is specified by the following equation:

(4–29)

where:

= elastic limit

, , b = material parameters characterizing the isotropic hardening behavior of materials

= equivalent plastic strain

The constitutive equations are based on linear isotropic elasticity, the von Mises yield function and the associated flow rule. The yield function is:

(4–30)

The plastic strain increment is:

(4–31)

where:

= plastic multiplier

The equivalent plastic strain increment is then:

(4–32)

The accumulated equivalent plastic strain is:

(4–33)

The power hardening law for nonlinear isotropic hardening behavior (accessed with TB,NLISO,,,,POWER) which is used primarily for ductile plasticity and damage is developed in the Gurson's Model:

(4–34)

where:

= current yield strength

= initial yield strength

= shear modulus

is the microscopic equivalent plastic strain and is defined by:

(4–35)

where:

= macroscopic plastic strain tensor

= rate change of variables

= Cauchy stress tensor

= inner product operator of two second order tensors

= porosity

This option uses the von Mises yield criterion with the associated flow rule and kinematic hardening (TB,PLASTIC,,,,BKIN).

The equivalent stress Equation 4–4 is therefore:

(4–36)

where = deviatoric stress vector:

(4–37)

where:

= mean or hydrostatic stress

= yield surface translation vector Equation 4–9

Because Equation 4–36 is dependent on the deviatoric stress, yielding is independent of the hydrostatic stress state. When is equal to the uniaxial yield stress, , the material is assumed to yield. The yield criterion Equation 4–7 is therefore:

(4–38)

The associated flow rule yields:

(4–39)

so that the increment in plastic strain is normal to the yield surface. The associated flow rule with the von Mises yield criterion is known as the Prandtl-Reuss flow equation.

The yield surface translation is defined as:

(4–40)

where:

= shear modulus

= Young's modulus (input as EX on MP command)

= Poisson's ratio (input as PRXY or NUXY on MP command)

The shift strain is calculated analogously to Equation 4–24:

(4–41)

where:

(4–42)

where:

= Young's modulus (input as EX on MP command)

= tangent modulus from the bilinear uniaxial stress-strain curve

The yield surface translation is initially zero and changes with subsequent plastic straining.

The equivalent plastic strain is dependent on the loading history and is defined to be:

(4–43)

where:

= equivalent plastic strain for this time point (output as EPEQ)

= equivalent plastic strain from the previous time point

The equivalent stress parameter is equal to the yield stress.

 

4.2.10.1. Applying an Initial Backstress

For bilinear kinematic hardening, shifting the yield center is possible by applying an initial backstress in the yield criteria. The yield function becomes:

(4–44)

and the associated flow rule is:

(4–45)

where is the initial backstress (defined via INISTATE). The equivalent stress becomes:

(4–46)

The effective backstress is still constituted according to Rice's hardening rule, which behaves as a linear relationship with the plastic strain. In the case of a non-zero initial backstress for this model, the total backstress does not maintain a straightforward linear relationship with the plastic strain. As a result, the yield center is naturally shifted due to the definition of .

This option (TB,PLASTIC,,,,KINH) uses the Besseling(54) model, also called the sublayer or overlay model (Zienkiewicz(55)), to characterize the material behavior. The material behavior is assumed to be composed of various portions (or subvolumes), all subjected to the same total strain, but each subvolume having a different yield strength. (For a plane stress analysis, the material can be thought to be made up of a number of different layers, each with a different thickness and yield stress.) Each subvolume has a simple stress-strain response but when combined the model can represent complex behavior. This allows a multilinear stress-strain curve that exhibits the Bauschinger (kinematic hardening) effect (Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options (b)).

The following steps are performed in the plasticity calculations:

The portion of total volume (the weighting factor) and yield stress for each subvolume is determined by matching the material response to the uniaxial stress-strain curve. A perfectly plastic von Mises material is assumed and this yields for the weighting factor for subvolume

(4–47)

where:

= weighting factor (portion of total volume) for subvolume and is evaluated sequentially from 1 to the number of subvolumes

= slope of the kth segment of the stress-strain curve (see Figure 4.5: Uniaxial Behavior for Multilinear Kinematic Hardening)

= sum of the weighting factors for the previously evaluated subvolumes

Figure 4.5: Uniaxial Behavior for Multilinear Kinematic Hardening

The yield stress for each subvolume is given by

(4–48)

where (, ) is the breakpoint in the stress-strain curve. The number of subvolumes corresponds to the number of breakpoints specified.

The increment in plastic strain for each subvolume is calculated using a von Mises yield criterion with the associated flow rule. The section on specialization for bilinear kinematic hardening is followed but since each subvolume is elastic-perfectly plastic, and therefore is zero.

The plastic strain increment for the entire volume is the sum of the subvolume increments:

(4–49)

where:

= number of subvolumes

The current plastic strain and elastic strain can then be calculated for the entire volume via Equation 4–20 and Equation 4–21.

The equivalent plastic strain (output as EPEQ) is defined by Equation 4–43 and equivalent stress parameter (output as SEPL) is calculated by evaluating the input stress-strain curve at (after adjusting the curve for the elastic strain component). The stress ratio (output as SRAT, Equation 4–25) is defined using the and values of the first subvolume.

The material model considered is a rate-independent version of the nonlinear kinematic hardening model proposed by Chaboche([245], [246]) (accessed via TB,CHABOCHE). The constitutive equations are based on linear isotropic elasticity, a von Mises yield function and the associated flow rule. Like the bilinear hardening option, the model can be used to simulate the monotonic hardening and the Bauschinger effect. The model is also applicable to simulate the ratcheting effect of materials. In addition, the model allows the superposition of several kinematic models as well as isotropic hardening models. It is thus able to model the complicated cyclic plastic behavior of materials, such as cyclic hardening or softening and ratcheting or shakedown.

The model uses the von Mises yield criterion with the associated flow rule, the yield function is:

(4–50)

where:

= isotropic hardening variable

According to the normality rule, the flow rule is written:

(4–51)

where:

= plastic multiplier

The backstress is superposition of several kinematic models as:

(4–52)

where:

= number of kinematic models to be superposed.

The evolution of the backstress (kinematic hardening rule) for each component is defined as:

(4–53)

where:

= material constants for kinematic hardening

The associated flow rule yields:

(4–54)

The plastic strain increment, Equation 4–51 is rewritten as:

(4–55)

The equivalent plastic strain increment is then:

(4–56)

The accumulated equivalent plastic strain is:

(4–57)

The isotropic hardening variable can be defined by:

(4–58)

where:

= elastic limit

, , = material constants characterizing the material isotropic hardening behavior.

The material hardening behavior in Equation 4–50 can also be defined via bilinear or multilinear isotropic hardening options, discussed earlier in Bilinear Isotropic Hardening.

The return mapping approach with consistent elastoplastic tangent moduli that was proposed by Simo and Hughes([252]) is used for numerical integration of the constitutive equation described above.

 

4.2.12.1. Applying an Initial Backstress

The Chaboche model supports an initial backstress definition (INISTATE,SET,DTYP,BSTR). The yield function in Equation 4–50 becomes:

(4–59)

Adhering to the Chaboche constitutive framework, only the associated flow rule changes:

(4–60)

This option is an extension of the linear Drucker-Prager yield criterion (input with TB,EDP). Both yield surface and the flow potential, (input with TBOPT on TB,EDP command) can be taken as linear, hyperbolic and power law independently, and thus results in either an associated or nonassociated flow rule. The yield surface can be changed with progressive yielding of the isotropic hardening plasticity material options, see hardening rule Figure 4.1: Stress-Strain Behavior of Each of the Plasticity Options (c) Bilinear Isotropic and (d) Multilinear Isotropic.

The yield function with linear form (input with TBOPT = LYFUN) is:

(4–61)

where:

= material parameter referred to pressure sensitive parameter (input as C1 on TBDATA command using TB,EDP)

where is the deviatoric Cauchy stress tensor

= yield stress of material (input as C2 on TBDATA command or input as TB,BISO, TB,NLISO, or TB,PLAST)

The yield function with hyperbolic form (input with TBOPT = HYFUN) is:

(4–62)

where:

= material parameter characterizing the shape of yield surface (input as C2 on TBDATA command using TB,EDP)

The yield function with power law form (input with TBOPT = PYFUN) is:

(4–63)

where:

= material parameter characterizing the shape of yield surface (input as C2 on TBDATA command using TB,EDP):

Similarly, the flow potential for linear form (input with TBOPT = LFPOT) is:

(4–64)

The flow potential for hyperbolic form (input with TBOPT = HFPOT) is:

(4–65)

The flow potential for power law form (input with TBOPT = PFPOT) is:

(4–66)

The plastic strain is defined as:

(4–67)

where:

= plastic multiplier

When the flow potential is the same as the yield function, the plastic flow rule is associated, which in turn results in a symmetric stiffness matrix. When the flow potential is different from the yield function, the plastic flow rule is nonassociated, and this results in an unsymmetric material stiffness matrix. By default, the unsymmetric stiffness matrix (accessed by NROPT,UNSYM) will be symmetricized.

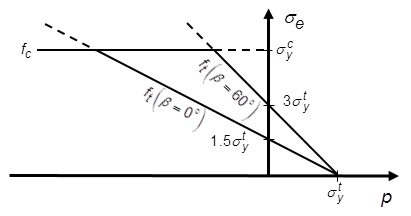
The cap model focuses on geomaterial plasticity resulting from compaction at low mean stresses followed by significant dilation before shear failure ([383]). A three-invariant cap plasticity model with three smooth yielding surfaces including a compaction cap, an expansion cap, and a shear envelope proposed by Pelessone ([384]) is described here.

Geomaterials typically have much higher triaxial strength in compression than in tension. The cap model accounts for this by incorporating the third-invariant of stress tensor (J₃) into the yielding functions.

Introduced first are functions to be used in the cap model, including shear failure envelope function, compaction cap function, expansion cap function, the Lode angle function, and hardening functions. Then, a unified yielding function for the cap model that is able to describe all the behaviors of shear, compaction, and expansion yielding surfaces is derived using the shear failure envelope and cap functions.

 

4.2.14.1. Shear Failure Envelope Function

A typical geomaterial shear envelope function is based on the exponential format given below:

(4–68)

where:

= first invariant of Cauchy stress tensor

subscript s = shear envelope function

superscript y = yielding related material constants

= current cohesion-related material constant (input using TB,EDP with TBOPT = CYFUN)

= material constants (input using TB,EDP with TBOPT = CYFUN)

Equation 4–68 reduces to the Drucker-Prager yielding function if parameter is set to zero. All material constants in Equation 4–68 are defined based on and , which are different from those in the previous sections. The effect of hydrostatic pressure on material yielding may be exaggerated at high pressure range by only using the linear term (Drucker-Prager) in Equation 4–68. Such an exaggeration is reduced by using both the exponential term and linear term in the shear function. Figure 4.6: Shear Failure Envelope Functions shows the configuration of the shear function. In Figure 4.6: Shear Failure Envelope Functions the dots are the testing data points, the finer dashed line is the fitting curve based on the Drucker-Prager linear yielding function, the solid curved line is the fitting curve based on Equation 4–68, and the coarser dashed line is the limited state of Equation 4–68 at very high pressures. In the figure is the current modified cohesion obtained by setting I₁ in Equation 4–68 to zero.

For positive values of , the shear envelope function of the EDP Cap model is evaluated at , giving the constant value .

Figure 4.6: Shear Failure Envelope Functions

 

4.2.14.2. Compaction Cap Function

The compaction cap function is formulated using the shear envelope function defined in Equation 4–68.

(4–69)

where:

= Heaviside (or unit step) function

subscript C = compaction cap-related function or constant

= ratio of elliptical x-axis to y-axis ( to )

= key flag indicating the current transition point at which the compaction cap surface and shear portion intersect.

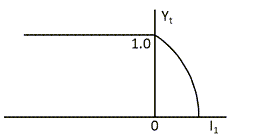
In Equation 4–69, is an elliptical function combined with the Heaviside function. is plotted in Figure 4.7: Compaction Cap Function.

This function implies:

1. When , the first invariant of stress, is greater than , the compaction cap takes no effect on yielding. The yielding may happen in either shear or expansion cap portion.

2. When is less than , the yielding may only happen in the compaction cap portion, which is shaped by both the shear function and the elliptical function.

Figure 4.7: Compaction Cap Function

 

4.2.14.3. Expansion Cap Function

Similarly, is an elliptical function combined with the Heaviside function designed for the expansion cap. is shown in Figure 4.8: Expansion Cap Function.

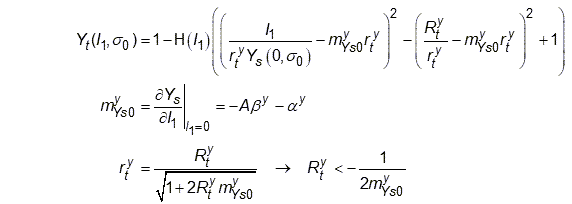(4–70)

where:

subscript t = expansion cap-related function or constant

This function implies that:

1. When is negative, the yielding may happen in either shear or compaction cap portion, while the tension cap has no effect on yielding.

2. When is positive, the yielding may only happen in the tension cap portion. The tension cap is shaped by both the shear function and by another elliptical function.

Equation 4–70 assumes that is only a function of and not a function of as is set to zero in function .

Figure 4.8: Expansion Cap Function

 

4.2.14.4. Lode Angle Function

Unlike metals, the yielding and failure behaviors of geomaterials are affected by their relatively weak (compared to compression) tensile strength. The ability of a geomaterial to resist yielding is lessened by nonuniform stress states in the principal directions. The effect of reduced yielding capacity for such geomaterials is described by the Lode angle and the ratio of triaxial extension strength to compression strength. The Lode angle can be written in a function of stress invariants and :

(4–71)

where:

and = second and third invariants of the deviatoric tensor of the Cauchy stress tensor.

The Lode angle function is defined by:

(4–72)

where:

= ratio of triaxial extension strength to compression strength

The three-invariant plasticity model is formulated by multiplying in the yielding function by the Lode angle function described by Equation 4–72. The profile of the yielding surface in a three-invariant plasticity model is presented in Figure 4.9: Yielding Surface in π-Plane.

Figure 4.9: Yielding Surface in π-Plane

 

4.2.14.5. Hardening Functions

The cap hardening law is defined by describing the evolution of the parameter , the intersection point of the compaction cap and the axis. The evolution of is related only to the plastic volume strain . A typical cap hardening law has the exponential form proposed in Fossum and Fredrich([93]):

(4–73)

where:

= initial value of at which the cap takes effect in the plasticity model.

= maximum possible plastic volumetric strain for geomaterials.

Parameters and have units of 1 / (Force / Length) and 1 / (Force / Length)², respectively. All constants in Equation 4–73 are non-negative.

Besides cap hardening, another hardening law defined for the evolution of the cohesion parameter used in the shear portion described in Equation 4–68 is considered. The evolution of the modified cohesion is assumed to be purely shear-related and is the function of the effective deviatoric plastic strain :

(4–74)

The effective deviatoric plastic strain is defined by its rate change as follows:

(4–75)

where:

= plastic strain tensor

= rate change of variables

= second order identity tensor

The unified and compacted yielding function for the cap model with three smooth surfaces is formulated using above functions as follows:

(4–76)

where:

= function of both and

Again, the parameter is the intersection point of the compaction cap and the axis. The parameter is the state variable and can be implicitly described using and given below:

(4–77)

The yielding model described in Equation 4–76 is used and is drawn in the and plane in Figure 4.10: Cap Model.

Figure 4.10: Cap Model

The cap model also allows non-associated models for all compaction cap, shear envelope, and expansion cap portions. The nonassociated models are defined through using the yielding functions in Equation 4–76 as its flow potential functions, while providing different values for some material constants. It is written below:

(4–78)

where:

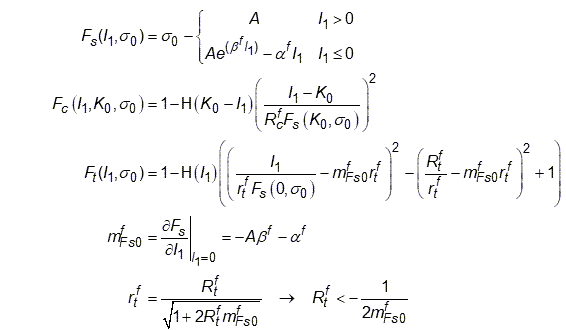(4–79)

where:

superscript f = flow-related material constant

This document refers to the work of Schwer ([385]) and Foster ([386]) for the numerical formulations used in the Pelessone ([384]) smooth cap plasticity model. Ansys, Inc. developed a new material integrator that is able to achieve a faster convergence rate for the transition zone between the cap and shear portions.

The flow functions in Equation 4–78 and Equation 4–79 are obtained by replacing , , , and in Equation 4–76 and Equation 4–77 with , , , and . The nonassociated cap model is input by using TB,EDP with TBOPT = CFPOT.

Shear hardening can be taken into account on by providing (via TB,PLASTIC or TB,NLISO). The initial value of must be consistent to . This input regulates the relationship between the modified cohesion and the effective deviatoric plastic strain.

As the smooth models have more numerical advantages, it is often necessary to transfer nonsmooth caps such as the Sandler model ([383]) to a smooth model. To facilitate the model transformation from the nonsmooth cap model to the Pelessone smooth cap model ([384]), two simple and robust methods are used ([387]); rather than solving a group of nonlinear equations, the Ansys, Inc. implementation solves only one scalar nonlinear equation.

Calibrating CAP Constants

Calibrating the CAP constants , , , , , and the hardening input for differs significantly from the other EDP options. The CAP parameters are all defined in relation to and , while the other EDP coefficients are defined according to and .

The Gurson model is used to represent plasticity and damage in ductile porous metals. The model theory is based on Gurson([363]) and Tvergaard and Needleman([364]). When plasticity and damage occur, ductile metal goes through a process of void growth, nucleation, and coalescence. Gurson’s method models the process by incorporating these microscopic material behaviors into macroscopic plasticity behaviors based on changes in the void volume fraction (porosity) and pressure. A porosity index increase corresponds to an increase in material damage, which implies a diminished material load-carrying capacity.

The microscopic porous metal representation in Figure 4.11: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale(a), shows how the existing voids dilate (a phenomenon, called void growth) when the solid matrix is in a hydrostatic-tension state. The solid matrix portion is assumed to be incompressible when it yields, therefore any material volume growth (solid matrix plus voids) is due solely to the void volume expansion.

The second phenomenon is void nucleation which means that new voids are created during plastic deformation. Figure 4.11: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale(b), shows the nucleation of voids resulting from the debonding of the inclusion-matrix or particle-matrix interface, or from the fracture of the inclusions or particles themselves.

The third phenomenon is the coalescence of existing voids. In this process, shown in Figure 4.11: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale(c), the isolated voids establish connections. Although coalescence may not discernibly affect the void volume, the load carrying capacity of this material begins to decay more rapidly at this stage.

Figure 4.11: Growth, Nucleation, and Coalescence of Voids in Microscopic Scale

The evolution equation of porosity is given by

(4–80)

where:

= porosity

= rate change of variables

The evolution of the microscopic equivalent plastic work is:

(4–81)

where:

= microscopic equivalent plastic strain

= Cauchy stress

= inner product operator of two second order tensors

= macroscopic plastic strain

= current yielding strength

The evolution of porosity related to void growth and nucleation can be stated in terms of the microscopic equivalent plastic strain, as follows:

(4–82)

where:

= second order identity tensor

The void nucleation is controlled by either the plastic strain or stress, and is assumed to follow a normal distribution of statistics. In the case of strain-controlled nucleation, the distribution is described in terms of the mean strain and its corresponding deviation. In the case of stress-controlled nucleation, the distribution is described in terms of the mean stress and its corresponding deviation. The porosity rate change due to nucleation is then given as follows:

(4–83)

where:

= volume fraction of the segregated inclusions or particles

= mean strain

= strain deviation

= mean stress

= stress deviation (scalar with stress units)

= pressure

It should be noted that "stress controlled nucleation" means that the void nucleation is determined by the maximum normal stress on the interfaces between inclusions and the matrix. This maximum normal stress is measured by . Thus, more precisely, the "stress" in the mean stress refers to . This relationship better accounts for the effect of triaxial loading conditions on nucleation.

Given Equation 4–80 through Equation 4–83, the material yielding rule of the Gurson model is defined as follows:

(4–84)

where:

, , and = Tvergaard-Needleman constants

= yield strength of material

= equivalent stress

, the Tvergaard-Needleman function is:

(4–85)

where:

= critical porosity

= failure porosity

The Tvergaard-Needleman function is used to model the loss of material load carrying capacity, which is associated with void coalescence. When the current porosity reaches a critical value , the material load carrying capacity decreases more rapidly due to the coalescence. When the porosity reaches a higher value , the material load carrying capacity is lost completely. The associative plasticity model for the Gurson model has been implemented.

 

4.2.15.1. Gurson Plasticity with Isotropic/Chaboche Kinematic Hardening

Gurson's model accounts for hydrostatic pressure and material isotropic hardening effects on porous metals. The Chaboche model is essentially the von Mises plasticity model incorporating Chaboche-type kinematic hardening.

The Gurson-Chaboche model, also used for modeling porous metals, is an extension of the Gurson model, combining both material isotropic and kinematic hardening. The model is based on the work of Mϋhlich and Brocks ([427]).

The yielding function of the Gurson-Tvergaard and Needleman model is modified as follows:

(4–86)

where:

is the total effective backstress, and the total backstress is the summation of several sub-backstresses:

where the evolution of each sub-backstress is defined by the Chaboche kinematic law:

(4–87)

The evolution of the equivalent plastic strain is defined through:

This model first requires the input parameters for Gurson plasticity with isotropic hardening, and then additional input parameters for Chaboche kinematic hardening. For more information, see Hardening in the Material Reference.

The cast iron plasticity model is designed to model gray cast iron. The microstructure of gray cast iron can be looked at as a two-phase material, graphite flakes inserted into a steel matrix (Hjelm([334])). This microstructure leads to a substantial difference in behavior in tension and compression. In tension, the material is more brittle with low strength and cracks form due to the graphite flakes. In compression, no cracks form, the graphite flakes behave as incompressible media that transmit stress and the steel matrix only governs the overall behavior.

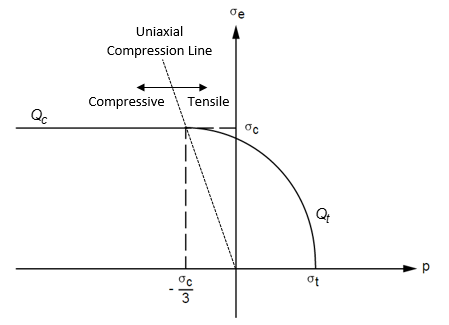
The model assumes isotropic elastic behavior, and the elastic behavior is assumed to be the same in tension and compression. The plastic yielding and hardening in tension may be different from that in compression. (See Figure 4.12: Idealized Response of Gray Cast Iron in Tension and Compression.)

Figure 4.12: Idealized Response of Gray Cast Iron in Tension and Compression

Yield Criteria

A composite yield surface is used to describe the different behavior in tension and compression. The tension behavior is pressure-dependent and the Rankine maximum stress criterion is used. The compression behavior is pressure-independent and the von Mises yield criterion is used. In principal stress space, the yield surface is a cylinder with a tension cutoff (cap). Figure 4.13: Cross-Section of Yield Surface shows a cross section of the yield surface on principal deviatoric-stress space and Figure 4.14: Yield Surface in the Meridional Plane shows the composite yield surface in the meridional plane.

Figure 4.13: Cross-Section of Yield Surface

(Viewed along the hydrostatic pressure axis)

Figure 4.14: Yield Surface in the Meridional Plane

The yield surface for tension and compression "regimes" are described by Equation 4–88 and Equation 4–89 (Chen and Han([332])).

The yield function for the tension cap is:

(4–88)

and the yield function for the compression regime is:

(4–89)

where:

= hydrostatic pressure

= von Mises equivalent stress

= deviatoric stress tensor

= Lode angle

= second invariant of deviatoric stress tensor

= third invariant of deviatoric stress tensor

= tension yield stress

= compression yield stress

Flow Rule

The plastic strain increments are defined as:

(4–90)

where is the so-called plastic flow potential, which consists of the von Mises cylinder in compression and modified to account for the plastic Poisson's ratio in tension, and takes the form:

(4–91)

(4–92)

where:

= plastic Poisson's ratio (input via TB,CAST)

= flow potential in compression

= flow potential in tension

Experimental evidence suggests that is always less than 0.5. For = 0.5, Equation 4–92 reduces to the von Mises cylinder. The flow potentials in the meridional plane are shown in this figure:

Figure 4.15: Flow Potential for Cast Iron

The region to the left of the uniaxial compression line is the compressive flow potential, while the region to the right is the tensile flow potential. As the flow potential is different from the yield function (nonassociated flow rule), the resulting material Jacobian is unsymmetric.

Hardening

The yield stress in uniaxial tension, , depends on the equivalent uniaxial plastic strain in tension, , and the temperature . Also the yield stress in uniaxial compression, , depends on the equivalent uniaxial plastic strain in compression, , and the temperature .

To calculate the change in the equivalent plastic strain in tension, the plastic work expression in the uniaxial tension case is equated to general plastic work expression as:

(4–93)

where:

= plastic strain vector increment

The change in the equivalent plastic strain in compression is defined as:

(4–94)

where: