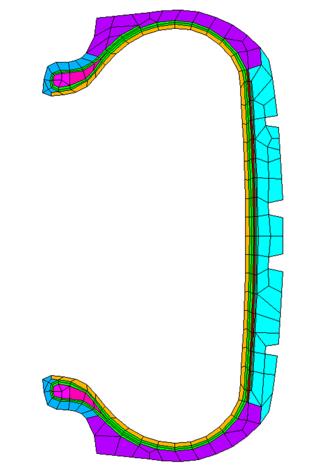
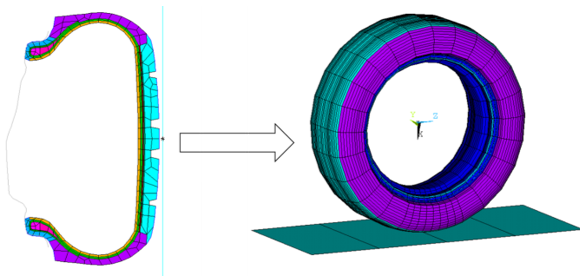
The 2D axisymmetric tire model uses PLANE182 axisymmetric elements with torsion degrees of freedom (KEYOPT(3) = 6):
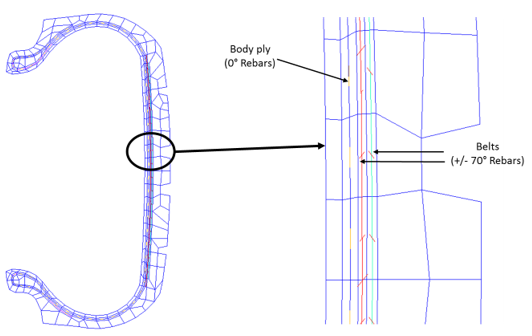
Reinforcings in the belt and body-ply regions are modeled with REINF263 smeared-reinforcing elements:
Two methods are available for defining the reinforcings:
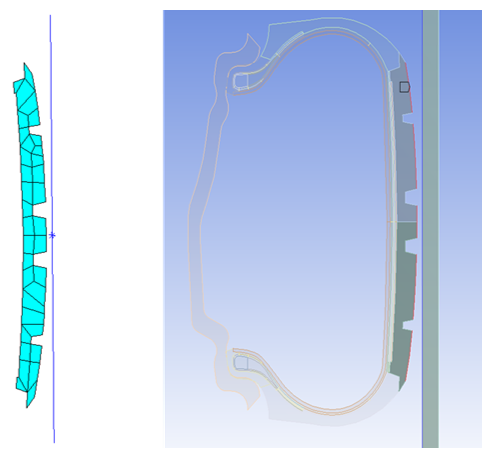
For the purpose of demonstration, both methods for defining reinforcing are used in this problem. The belt 1 reinforcings are created via the mesh-independent method, and the belt 2 reinforcings are created via the standard method.
The mesh-independent method for defining reinforcing offers much flexibility when the base elements (PLANE182 in this case) are arbitrary and have no distinct patterns for the reinforcing to attach.
The reinforcing location is represented via a mesh with
MESH200 elements. Other model information (such as
reinforcing material, cross-section area, spacing, and orientation) can be
provided by a reinforcing element (REINFnnn) section
(SECDATA) or MESH200 element
data.
In the 2D axisymmetric model, line geometries meshed with MESH200 can be used as reinforcing locations in the belt and body-ply regions.
For more information, see Mesh-Independent Method for Defining Reinforcing in the Structural Analysis Guide.
Example 57.1: Using the Mesh-Independent Method to Create Reinforcings in the Belt 1 Region
! Create reinforcing elements at Belt_1 a1 = 0.22e-06 ! Cross-section area s1=1.1e-03 ! Spacing m1=10 ! Material number sectype,9,reinf,smear secdata,m1,a1,s1,,-70,mesh ! Use "Mesh" pattern et,2,200 keyopt,2,1,0 secn,9 ! Use reinforcing section for Mesh200 mat,m1 type,2 lsel,s,,,355,358 ! Select lines representing reinforcing locations cm,belt1_lines,line lmesh,all ! Mesh selected lines with MESH200 allsel,below,line cm,belt1_mesh200,elements allsel,all cmsel,s,belt1 ! Select base elements in the belt1 region cmsel,a,belt1_mesh200 ! Select MESH200 elements mat,m1 ereinf ! Create reinforcing elements allsel,all ! Delete Mesh200 elements after creating the reinforcing elements: cmsel,s,belt1_lines lclear,all,all etdel,2 allsel,all
The standard method for defining reinforcing is convenient when the base elements (PLANE182 in this case) have a consistent element orientation. The reinforcing location is directly defined with respect to the connectivity and orientation of the base elements. For more information, see Standard Method for Defining Reinforcing in the Structural Analysis Guide.
Example 57.2: Using the Standard Method to Create Reinforcings in the Belt 2 Region
! Creating reinforcing elements at Belt_2 a2 = 0.22e-06 ! Cross-section area s2=1.1e-03 ! Spacing m2=10 ! Material number sectype,11,reinf,smear secdata,m2,a2,s2,,70,edgo,1,.5 cmsel,s,belt2 ! Select base elements in the belt2 region eplot secnum,11 mat,10 ereinf ! Create reinforcing elements allsel,all
The 2D axisymmetric tire model has two contact pairs:
Between the rim and the tire
Between the road and the tire
The contact pair between the rim and the tire is initially made as a frictionless contact pair in the 2D axisymmetric model:
After the 2D axisymmetric analyses, the contact pair is converted to a bonded type contact pair for further analyses on the 3D model, as no relative motion is needed between the rim and the tire during steady-state rolling.
The rim is modeled as a rigid body. If required during the 2D to 3D analysis, other contact settings for this contact pair can be changed. In this example problem, convergence issues during rebalancing are resolved by adjusting the pinball radius.
The contact pair between the road and the tire plays no role in the 2D axisymmetric analyses:
After the 2D axisymmetric analyses when the model is extruded to 3D, this contact pair is converted for the 3D model. Initially, the contact pair is frictionless. During the steady-state rolling load step on the 3D model, the coefficient of friction is gradually increased from 0 to 1.
The contact pair uses a default value representing the allowable elastic slip (SLTO). If problems occur when trying to obtain a free-rolling solution, you can override the default SLTO values by defining a scaling factor (a positive value when using command input) or an absolute value (a negative value when using command input).
After the rim-mounting and inflation analyses on the 2D model, both contact pairs are extruded when the 2D model is converted to the 3D model. The rim surface is extruded in the circumferential direction, and the road surface is extruded in the global Z direction:
After performing the analyses on the 2D model, some contact settings for the contact pairs can be modified if necessary. For example:
The coefficient of friction is introduced for the road-tire contact pair in the steady-state rolling analysis only.
The behavior of the rim-tire contact is changed from frictionless in the 2D model to bonded in the 3D model.