This section provides information to help you perform a successful nonlinear analysis.
Ansys, Inc. recommends using current-technology elements for nonlinear analyses.
The following topics are available:
By taking your time and proceeding carefully, you can avoid many difficulties commonly associated with nonlinear analyses.
Consider these suggestions:
If you have not used a particular nonlinear feature before, construct a very simple model (containing only a few elements), and make sure you understand how to handle this feature before you use it in a large, complicated model.
Gain preliminary insight into your structure's behavior by analyzing a preliminary simplified model first. For nonlinear static models, a preliminary linear static analysis can reveal which regions of your model will first experience nonlinear response, and at what load levels these nonlinearities will come into play. For nonlinear transient dynamic analyses, a preliminary model of beams, masses, and springs can provide insight into the structure's dynamics at minimal cost. Preliminary nonlinear static, linear transient dynamic, and/or modal analyses can also help you to understand various aspects of your structure's nonlinear dynamic response before you undertake the final nonlinear transient dynamic analysis.
Read and understand the program's output messages and warnings. At a minimum, before you try to postprocess your results, verify that your problem converged. For path-dependent problems, the printout's equilibrium iteration record can be especially important in helping you to determine if your results are valid or not.
Keep your final model as simple as possible. For example, if applicable to your analysis, try any or all of the following:
Represent your 3D structure as a 2D plane stress, plane strain, or axisymmetric model.
Reduce your model size by using symmetry or antisymmetry surfaces.
If your model is loaded antisymmetrically, however, you can generally not take advantage of antisymmetry to reduce a nonlinear model's size. Antisymmetry can also be rendered inapplicable by large deflections.
Omit a nonlinear detail if you can do so without affecting results in critical regions of your model.
Model transient dynamic loading in terms of static-equivalent loads.
Consider substructuring the linear portions of your model to reduce the computational effort required for intermediate load or time increments and equilibrium iterations.
Recognize that regions undergoing plastic deformation require a reasonable integration point density (mesh density is particularly important in plastic-hinge regions).
Provide an adequate mesh density on contact surfaces to allow contact stresses to be distributed in a smooth fashion. Likewise, provide a mesh density adequate for resolving stresses; areas where stresses or strains are of interest require a relatively fine mesh compared to that needed for displacement or nonlinearity resolution.
Use a mesh density adequate to characterize the highest mode shape of interest. The number of elements needed depends on the elements' assumed displacement shape functions, as well as on the mode shape itself. Also, use a mesh density adequate to resolve any transient dynamic wave propagation through your structure; if wave propagation is important, then provide at least 20 elements to resolve one wavelength.
For nonconservative, path-dependent systems, you need to apply the load in small enough increments to ensure that your analysis closely follows the structure's load-response curve.
You can sometimes improve the convergence behavior of conservative systems by applying the load gradually, so as to minimize the number of Newton-Raphson equilibrium iterations required.
This section provides information to help you fix convergence problems in a nonlinear analysis. The following topics are available:
- 8.12.2.1. Overview of Convergence Problems
- 8.12.2.2. Performing Nonlinear Diagnostics
- 8.12.2.3. Tracking Convergence Graphically
- 8.12.2.4. Automatic Time-Stepping
- 8.12.2.5. Line Search
- 8.12.2.6. Nonlinear Stabilization
- 8.12.2.7. Arc-Length Method
- 8.12.2.8. Artificially Inhibit Divergence in Your Model's Response
- 8.12.2.9. Use the Nonlinear Adaptivity Feature
- 8.12.2.10. Dispense with Extra Element Shapes
- 8.12.2.11. Using Element Birth and Death Wisely
- 8.12.2.12. Read Your Output
- 8.12.2.13. Graph the Load and Response History
- 8.12.2.14. Semi-Implicit Method
- 8.12.2.15. Solution Transition Method
When performing a nonlinear analysis you may encounter convergence difficulties due to a number of reasons. Some examples may be initially open contact surfaces causing rigid body motion, large load increments causing nonconvergence, material instabilities, or large deformations causing mesh distortion that result in element shape errors. The program automatically adjusts solution parameters and attempts to obtain a robust, accurate solution. In addition, several tools are available to help you identify potential problems before, during, and after a solution.
CHECK, MCHECK, and CNCHECK commands help you verify if there are any obvious problems with the model before you start the solution. The CHECK command does an overall verification of the model, including missing elastic properties, unconstrained model, and element shape checks. The MCHECK command can help you identify defects in the mesh such as holes or cracks, especially when the mesh is imported from a third party software. The CNCHECK command provides the initial contact status of contact pairs, identifying whether the contacts are initially open or closed. If, for example, a part in your model is constrained only through contact with other parts and if the contact surfaces are open, the CNCHECK command can help you identify this potential error condition.
When you analyze models with large deformations, some portions of the initial mesh can become highly distorted. Highly distorted elements can take on unacceptable shapes, providing inaccurate results. This can cause your nonlinear solution to stop. When this happens, use the ESCHECK command to perform shape checking of deformed elements in the postprocessor (based on the current set of results in database). This deformed-shape checker helps you to identify the portions of your model that require different meshing, thereby allowing them to retain acceptable shapes. Using ESCHECK at different time points helps you to identify the load conditions that cause mesh deterioration.
A convergence failure can also indicate a physical instability in the structure, or it can merely be the result of some numerical problem in the finite element model.
The following sections detail some of the techniques that you can use to attempt to improve the convergence performance of your analysis.
The nonlinear diagnostics tool NLDIAG can help you find problems in your model when an analysis does not converge.
Identify Regions of High Residual Forces — Issue the NLDIAG,NRRE command to write the
Newton-Raphson residuals from equilibrium iterations to a file
(Jobname.nrxxx
). You can then contour plot the residual forces via the
PLNSOL,NRRE command, which helps to identify regions
of high residual forces.
Such a capability can be useful when you experience convergence difficulties in the middle of a load step, where the model has a large number of contact surfaces and other nonlinearities. You can restart the analysis and issue an NLDIAG,NRRE command to write out the residuals. By tracking the way the residuals change over several equilibrium iterations you can identify a portion of your model where large residuals persist. You can then focus on the nonlinearities in that area (for example, a contact pair's properties) instead of having to deal with the entire model.
Identify Problem Elements — Typically, nonlinear analyses fail to converge for the following reasons:
Too large a distortion
Elements contain nodes that have near zero pivots (nonlinear analyses)
Too large a plastic or creep strain increment
Elements where mixed u-P constraints are not satisfied (mixed u-P option of current-technology solid elements only)
Hyperelastic element (EPHY), cohesive zone material (EPCZ), or damage strain (EPDM) not converged
Radial displacement (RDSP) not converged
MPC184 multipoint constraint elements (184J) using the Lagrangian multiplier option fail to satisfy constraint conditions
The program has default limits which, when exceeded, determine when convergence criteria have been violated. Some limits are user-controlled; for example, the CUTCONTROL command sets the maximum plastic/creep strain increments allowed in an iteration. Other limits are fixed.
The NLDIAG,EFLG command identifies elements that violate
the above criteria and records them in a file
(Jobname.ndxxx
).
Convergence problems may occur when material algorithms fail (for example, local element level Newton-Raphson convergence failure, or extreme element distortion). The error message identifies the corresponding element number and/or the material ID for these cases. Be sure to read any error messages generated during solution.
Process the Tracked Results — Issue the NLDPOST command to process the
.nd
xxx nonlinear diagnostics files. The command
creates components of elements that violate a certain criterion for a
particular equilibrium iteration (or iterations).
Identify contact pairs causing convergence difficulties — Issue the NLDIAG,CONT command to write various contact information for all defined contact pairs to a single Jobname.cnd text file. The file is written during solution at a user-specified frequency (each iteration, substep, or load step).
Information stored in this file helps identify when and how contact occurs, determine the regions where contact is unstable, and identify the corresponding contact parameters. You can then focus on the specific settings for those particular contact pairs that need attention.
Monitor the Diagnostics Results in Real Time — The NLHIST command enables you to monitor results of interest in real time during solution. Before starting the solution, you can request nodal data such as displacements or reaction forces at specific nodes. You can also request element nodal data such as stresses and strains at specific elements to be graphed. Pair-based contact data are also available. The result data are written to a file named Jobname.nlh.
For example, a reaction force-deflection curve could indicate when possible buckling behavior occurs. Nodal results and contact results are monitored at every converged substep while element nodal data are written as specified via the OUTRES setting.
You can also track results during batch runs. Either access the Launcher and select from the menu, or type nlhist242 at the command line. Use the supplied file browser to navigate to your Jobname.nlh file, and click on it to invoke the tracking utility. You can use this utility to read the file at any time, even after the solution is complete (the data in the file must be formatted correctly).
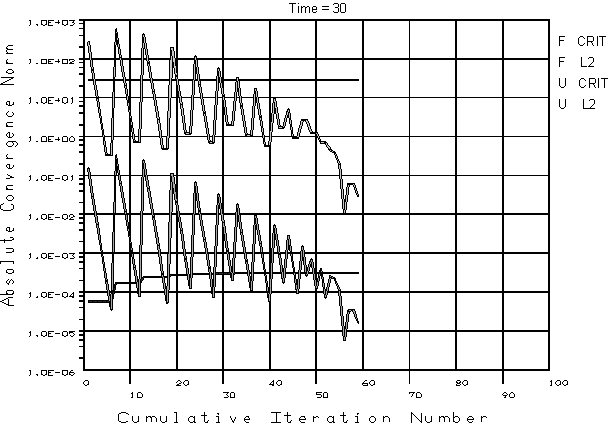
As a nonlinear structural analysis proceeds, the program calculates convergence norms with corresponding convergence criteria each equilibrium iteration. Available in both batch and interactive sessions, the Graphical Solution Tracking (GST) feature displays the computed convergence norms and criteria while the solution is in process. By default, GST is ON for interactive sessions and OFF for batch runs. To turn GST on or off, use either of the following:
Figure 8.21: Convergence Norms Displayed By the Graphical Solution Tracking (GST) Feature shows a typical GST display:
Place an upper limit on the time-step size (DELTIM or NSUBST), especially for complicated models. Doing so ensures that all of the modes and behaviors of interest are accurately included. This can be important in the following situations:
Problems that have only localized dynamic behavior (for example, turbine blade and hub assemblies) in which the low-frequency energy content of the system could dominate the high-frequency areas.
Problems with short ramp times on some of their loads. If the time-step size is allowed to become too large, ramped portions of the load history may be inaccurately characterized.
Problems that include structures that are continuously excited over a range of frequencies (for example, seismic problems).
Exercise caution when modeling kinematic structures (systems with rigid-body motions). These following guidelines can usually help you to obtain a good solution:
Incorporate significant numerical damping (0.05 < γ < 0.1 on the TINTP command) into the solution to filter out the high frequency noise, especially if a coarse time step is used. Do not use α-damping (mass matrix multiplier, ALPHAD command) in a dynamic kinematic analysis, as it dampens the rigid body motion (zero frequency mode) of the system.
Avoid imposed displacement history specifications, because imposed displacement input has (theoretically) infinite jumps in acceleration, which causes stability problems for the Newmark time-integration algorithm.
Line search (LNSRCH) can be useful for enhancing convergence, but it can be expensive (especially with plasticity). You might consider setting line search on in the following cases:
When your structure is force-loaded (as opposed to displacement-controlled).
If you are analyzing a "flimsy" structure which exhibits increasing stiffness (such as a fishing pole).
If you notice (from the program output messages) oscillatory convergence patterns.
You can use the nonlinear stabilization method to solve both locally and globally unstable problems, and to overcome convergence for general problems. For more information, see Using Nonlinear Stabilization.
You can use the arc-length method (ARCLEN and ARCTRM) to obtain numerically stable solutions for many physically unstable structures. For more information, see Using the Arc-Length Method.
If you do not want to use both nonlinear stabilization and the arc-length method to analyze a force-loaded structure that starts at, or passes through, a singular (zero stiffness) configuration, you can sometimes use other alternatives to artificially inhibit divergence in your model's response:
In some cases, you can use imposed displacements instead of applied forces. This approach can be used to start a static analysis closer to the equilibrium position, or to control displacements through periods of unstable response (for example, snap-through or postbuckling).
Another technique that can be effective in circumventing problems due to initial instability is running a static problem as a "slow dynamic" analysis (that is, using time-integration effects in an attempt to prevent the solution from diverging in any one load step).
You can also apply temporary artificial stiffness to unstable degrees of freedom, using control elements (such as COMBIN37), or using the birth and death option on other elements. The idea here is to artificially restrain the system during intermediate load steps in order to prevent unrealistically large displacements from being calculated. As the system displaces into a stable configuration, the artificial stiffness is removed.
If the solution fails to converge and the mesh is severely distorted, consider using nonlinear adaptivity, which repairs the distorted mesh automatically during simulation. For more information, see the Nonlinear Adaptivity Analysis Guide.
The program provides "incompatible" modes" formulation (also referred to as "extra shapes") for modeling bending applications. If your problem is predominantly bulk deformation, then you may choose to turn extra shapes off to reduce CPU/storage requirements and enhance convergence. However, doing so precludes the ability to model any bending.
Realize that any sudden change in your structure's stiffness matrix is likely to cause convergence problems. When activating or deactivating elements, try to spread the changes out over a number of substeps. (Use a small time-step size if necessary to accomplish this.) Also be aware of possible singularities (such as sharp reentrant corners) that might be created as you activate or deactivate elements. Such singularities can cause convergence problems.
The program performs a nonlinear analysis as a series of linear approximations with corrections. The program printout gives you continuous feedback on the progress of these approximations and corrections. (Printout either appears directly on your screen, is captured on Jobname.out, or is written to some other file (/OUTPUT).) You can examine some of this same information in POST1, using the PRITER command, or in POST26, using the SOLU and PRVAR commands. You should make sure that you understand the iteration history of your analysis before you accept the results. In particular, do not dismiss any program error or warning statements without fully understanding their meaning. A typical nonlinear output listing is shown in Figure 8.22: Typical Nonlinear Output Listing.
Figure 8.22: Typical Nonlinear Output Listing
| SOLVE command echo |
***** SOLVE COMMAND ***** |
| Checking Logic |
*** NOTE *** CP= 13.891 TIME= 11:09:22 Nonlinear analysis, NROPT set to 1 (full Newton-Raphson solution procedure) for all degrees of freedom. |
| Load step summary table |
L O A D S T E P O P T I O N S
LOAD STEP NUMBER. . . . . . . . . . . . . . . . 2
TIME AT END OF THE LOAD STEP. . . . . . . . . . 200.00
AUTOMATIC TIME-STEPPING . . . . . . . . . . . . ON
INITIAL NUMBER OF SUBSTEPS . . . . . . . . . 100
MAXIMUM NUMBER OF SUBSTEPS . . . . . . . . . 10000
MINIMUM NUMBER OF SUBSTEPS . . . . . . . . . 10
MAXIMUM NUMBER OF EQUILIBRIUM ITERATIONS. . . . 15
STEP CHANGE BOUNDARY CONDITIONS . . . . . . . . NO
TERMINATE ANALYSIS IF NOT CONVERGED . . . . . .YES (EXIT)
CONVERGENCE CONTROLS. . . . . . . . . . . . . .USE DEFAULTS
PRINT OUTPUT CONTROLS . . . . . . . . . . . . .NO PRINTOUT
DATABASE OUTPUT CONTROLS
ITEM FREQUENCY COMPONENT
BASI -10
|
| Load step 2 substep 1 |
FORCE CONVERGENCE VALUE = 0.2006E+06 CRITERION= 1125.
EQUIL ITER 1 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.1272E-01
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.1272E-01
FORCE CONVERGENCE VALUE = 4267. CRITERION= 480.2
EQUIL ITER 2 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= -0.9019E-03
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = -0.9019E-03
FORCE CONVERGENCE VALUE = 1751. CRITERION= 488.2
EQUIL ITER 3 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.1746E-03
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.1746E-03
FORCE CONVERGENCE VALUE = 778.5 CRITERION= 497.7
EQUIL ITER 4 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.6943E-04
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.6943E-04
FORCE CONVERGENCE VALUE = 347.4 CRITERION= 507.7 <<< CONVERGED
>>> SOLUTION CONVERGED AFTER EQUILIBRIUM ITERATION 4
*** LOAD STEP 2 SUBSTEP 1 COMPLETED. CUM ITER = 7
*** TIME = 101.000 TIME INC = 1.00000
|
| Load step 2 substep 2 |
FORCE CONVERGENCE VALUE = 0.6674E+05 CRITERION= 594.3
EQUIL ITER 1 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.4318E-02
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.4318E-02
FORCE CONVERGENCE VALUE = 626.2 CRITERION= 502.9
EQUIL ITER 2 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.8570E-04
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.8570E-04
FORCE CONVERGENCE VALUE = 77.87 CRITERION= 512.9 <<< CONVERGED
>>> SOLUTION CONVERGED AFTER EQUILIBRIUM ITERATION 2
*** LOAD STEP 2 SUBSTEP 2 COMPLETED. CUM ITER = 9
*** TIME = 102.000 TIME INC = 1.00000
|
| Load step 2 substep 3 Equilibrium iteration summaries |
FORCE CONVERGENCE VALUE = 0.1333E+05 CRITERION= 575.4
EQUIL ITER 1 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= -0.5329E-02
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = -0.5329E-02
FORCE CONVERGENCE VALUE = 8237. CRITERION= 534.2
EQUIL ITER 2 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.3628E-02
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.3628E-02
FORCE CONVERGENCE VALUE = 3905. CRITERION= 532.9
EQUIL ITER 3 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.1451E-02
LINE SEARCH PARAMETER = 1.000 SCALED MAX DOF INC = 0.1451E-02
FORCE CONVERGENCE VALUE = 1135. CRITERION= 540.3
EQUIL ITER 4 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.1034E-03
LINE SEARCH PARAMETER = 0.9578 SCALED MAX DOF INC = 0.9905E-04
FORCE CONVERGENCE VALUE = 41.95 CRITERION= 551.4 <<< CONVERGED
>>> SOLUTION CONVERGED AFTER EQUILIBRIUM ITERATION 4
|
| Substep summary |
*** LOAD STEP 2 SUBSTEP 3 COMPLETED. CUM ITER = 13
*** TIME = 103.500 TIME INC = 1.50000
|
This verification technique may be considered to be a graphical combination of two other techniques: checking for reasonableness, and reviewing the iteration history. POST26 graphs of load and response histories should agree with your informed expectations about your structure's behavior. The results of interest (displacements, reaction forces, stresses, and so on) should show relatively smooth response histories. Any non-smoothness may indicate that too coarse of a time step was used.
Analyses that experience brief periods of extreme nonlinearity (for example, models with local buckling or sudden changes in material constitutive behavior) can benefit from the semi-Implicit method (SEMIIMPLICIT command). By this method, the analysis starts out using an implicit solution scheme but transitions to a semi-implicit solution scheme when the implicit solution fails to converge. By using the semi-implicit approach to solve the brief period of nonlinear loading, the semi-implicit method increases the robustness of the implicit solution. For more information, see Semi-Implicit Method in the Advanced Analysis Guide.
The solution transition procedure is useful in overcoming convergence problems in some difficult implicit static analyses: for example, analyses that experience rigid body motion or local buckling.
By this procedure, the analysis starts out as a static solution and automatically transitions to a transient dynamic solution based on a user-defined criterion specified via the SOLOPTION command. Once the solution overcomes the convergence difficulty, the analysis may attempt to come back to a static solution based on a user-specified criterion for time spent in the transient phase.
For more information, see Automatic Transition Between Static and Transient Solutions in the Advanced Analysis Guide.