At the solution (SOLVE) stage of a cyclic symmetry analysis, the program applies the appropriate cyclic symmetry boundary conditions for each harmonic index solution requested (via the CYCOPT command) and solves. The program performs each harmonic index solution as a separate load step.
The following solution architecture topics are available for cyclic symmetry analysis:
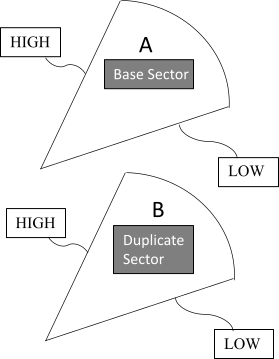
The architecture of the cyclic symmetry solution process depends upon how the compatibility and equilibrium conditions of the cyclic sector are enforced in the matrix-solution process. The two most common solution methods are Duplicate Sector and Complex Hermitian. For faster performance, the program uses the Duplicate Sector method.
During the solution stage, the program generates a duplicate sector of elements at the same geometric location as the base sector. (Duplicate sector creation occurs automatically and transparently.) The program applies all loading, boundary conditions, and coupling and constraint equations present on the base sector to the duplicate sector.
The program enforces cyclic symmetry compatibility conditions for each harmonic index solution via coupling and/or constraint equations (CEs) connecting the nodes on the low- and high-edge components on the base and duplicate sectors. The program deletes the coupling and/or constraint equations after each harmonic index solution, preserving any internal coupling and constraint equations that you may have defined on the base sector for subsequent analyses. The constraint equations for edge-component nodes have the form shown in Equation 3–1.
Note: These internal CEs cannot be listed or viewed after a cyclic symmetry solution.
During the solution stage of a cyclic symmetry analysis, the program automatically rotates the nodal coordinate systems of all nodes on the low and high sector edges to be parallel with the cyclic coordinate system.
 | (3–1) |
where,
 = Harmonic index -- (0,1,2,…, / 2) when  is even, (0,1,2,…,( -1) / 2) when  is odd. ( is an integer representing the number of sectors in
360°.) |
 = Sector angle ( ) |
 = Vector of displacement and rotational degrees of
freedom |
 represents the base
sector low side edge |
 represents the base
sector high side edge |
 represents the duplicate
sector low side edge |
 represents the duplicate
sector high side edge |
The equation is a function of harmonic index k
generating different sets of constraint equations for each harmonic index.
Therefore, for each harmonic index solution requested, the program creates the
appropriate constraint equations automatically, connects the edge-component nodes on
base sector A and duplicate sector B, and solves.
Constraint equations that tie together the low and high edges of your model are generated from the low- and high-edge components, and nowhere else. You should verify that automatically detected components are in the correct locations and that you are able to account for all components; to do so, you can list (CMLIST) or plot (CMPLOT) the components.
Non-cyclically symmetric loading is applicable to static and full harmonic cyclic solutions. A load is non-cyclically symmetric when it varies between sectors and involves at least one harmonic index greater than zero. Support is available for cyclic analyses that have some combination of cyclically symmetric and non-cyclically symmetric loading.
The arbitrary forces acting on an equivalent full system can be modeled as the sum of a finite number of spatial Fourier harmonics in cyclic symmetry. The structure for each spatial harmonic index is formed by applying constraint equations between the base sector and duplicate sector. For each spatial Fourier harmonic of the cyclic symmetry model, a corresponding set of equations is solved and expanded. The arbitrary forces are projected into each harmonic space and used to calculate the response for each harmonic. The responses for each harmonic are summed to give the complete response of the equivalent full system. For more information, see Cyclic Symmetry Transformations in the Mechanical APDL Theory Reference.
Table 3.1: Valid Non-Cyclically Symmetric Loads
| Non-cyclically symmetric load type | Commands | Loads | Comments |
|
Nodal Loads |
following the sector specifications
(CYCOPT,LDSECT, |
FX, FY, and FZ |
HFLOW is blocked for sector-restricted loading but can follow afterwards. All other nodal loads are not supported for non-cyclically symmetric loading. |
|
Surface Loads |
following the sector specifications
(CYCOPT,LDSECT, |
PRES |
CONV is blocked for sector-restriced loading but can follow afterwards. All other surface loads are not supported for non-cyclically symmetric loading. |
|
Inertia Loads |
Applies to all sectors. (Not affected by
CYCOPT,LDSECT, Default load in global X, Y, and Z on all sectors. |
May require harmonic index 0 and/or 1 only. |
Note: When cyclically-symmetric loading is applied, non-cyclically symmetric loading defined using the CYCOPT,LDSECT command is ignored. If a combination of cyclically-symmetric and non-cyclically symmetric loading is desired, both types must be applied using the CYCOPT,LDSECT command.
This section is applicable to static and full harmonic cyclic analyses only. For cyclic mode-superposition harmonic analyses, non-cyclically symmetric loading is applied in a different manner. For more information, see Mode-Superposition Harmonic Cyclic Symmetry Analysis.
You can apply arbitrary non-cyclically symmetric loads in one of two ways:
Any other load definition defines a cyclically-symmetric load.
3.1.3.1.1. Using CYCOPT,LDSECT
You can specify non-cyclically symmetric loading via the LDSECT (load-on-sector) value on the CYCOPT command. A value greater than 0 (the default, indicating that the loads are identical on all sectors) restricts subsequently defined force loads and surface loads to the specified sector. The restriction remains in effect until you change or reset it by issuing a subsequent CYCOPT command. See Example 3.1: Non-Cyclically Symmetric Loading via Automatically-Defined Tabular Load.
Example 3.1: Non-Cyclically Symmetric Loading via Automatically-Defined Tabular Load
CYCOPT,LDSECT,1 ! Subsequent loads are applied on sector 1 only SFL,ALL,PRES,10000
To delete a previously applied load on a specified sector, issue an FDELE command. See Example 3.2: Deleting a Sector Load.
Example 3.2: Deleting a Sector Load
CYCOPT,LDSECT,3 F,10,UX,1E6 ! Apply FX=1E6 at node 10 on sector 3 ... FDELE,10,UX ! Delete FX at node 10 on sector 3
When using CYCOPT,LDSECT, the program automatically stores the non-cyclically symmetric load in a table with SECTOR as the primary variable. The table cannot reference any other independent variable (for example, TEMP). You must directly define the table for any BC table requiring more than one independent variable – see Directly Defining Tabular Load with SECTOR as the Primary Variable.
You can apply non-cyclically symmetric loads directly as tabular data via the *DIM command, setting SECTOR as the primary variable (for an in-depth discussion on entering tabular data, see Tabular Input via Table Array Parameters in the Ansys Parametric Design Language Guide). See Example 3.3: Non-Cyclically Symmetric Loading via User-Defined Tabular Load.
Example 3.3: Non-Cyclically Symmetric Loading via User-Defined Tabular Load
*DIM,S1PRES,TABLE,5,1,1,SECTOR ! Model has 5 sectors *SET,S1PRES(1,0,1),1,2,3,4,5 *SET,S1PRES(1,1,1),10000,0,0,0,0 ! Pressure is applied on sector 1 only SFL,ALL,PRES,%S1PRES%
The program assumes any tabular load referencing SECTOR to be non-cyclically symmetric although it could be identical on all sectors.
Unlike other tabular data, a table with SECTOR as the primary variable is not interpolated over the sectors. You must specify the load for all sectors and give a value of zero to the sectors with no load to ensure correct results.
When combined with other independent variables, SECTOR can be in position 1, 2, or 3 only.
Any tabular data X, Y, or Z variation applied to a cyclic model may not be applied in the same manner in which such a variation would occur for an equivalent full model (the exception being a variation in the axial direction). For example, if a tabular value of a nodal force is applied as a function of the tabular variable Y, the program applies it to the designated cyclic sectors using values based upon the Y values of the base sector only.
A given high-edge node is usually at the same location in the structure as the corresponding low-edge node of the adjacent sector; therefore, it is necessary to apply constraints consistently. Note that inconsistent constraints are impossible to satisfy if the solution remains cyclic. The results can be unpredictable.
If a high (or low)-edge DOF has a constant (non-tabular) constraint, and the corresponding low (or high)-edge DOF is unconstrained, the program copies the constraint to the opposite edge. If a high (or low)-edge DOF has a tabular constraint, and the corresponding low (or high)-edge DOF is unconstrained, the program stops the solution with an error message. If a high-low corresponding pair of DOF are both constrained in any manner, the program assumes that you have specified constraints in a consistent manner.
One warning is issued the first time this is done for a given SOLVE operation.
Because edge nodes are rotated into the cyclic coordinate system during solution, any applied displacements or forces on sector edges will be in the cyclic coordinate system.
You should apply non-cyclically symmetric nodal loads only to nodes with one of the following conditions:
Nodes that are not rotated. The default nodal coordinate system is the global Cartesian except for the cyclic edge nodes, which are internally rotated into the cyclic coordinate system during solution.
Nodes that are rotated into the cyclic symmetry coordinate system.
Applying non-cyclically symmetric loads to nodes with other arbitrary nodal rotations may result in unexpected results.
Surface loads must be applied in the standard, non-rotated element coordinate system so that surface loads are applied normal or tangential to the element surface. The rotation of the load will be cyclic in nature because the load direction will rotate with the element for each sector. You can create non-cyclically symmetric surface loads only by changing the magnitude of the normal and tangential surface loads, rather than changing their direction. Application of surface loads using a coordinate system other than the standard, non-rotated element coordinate system may generate unexpected results.
You can plot non-cyclically symmetric boundary conditions (BCs) on the sector on which the BC (F, D, SF) is applied. By expanding the cyclic sector model plot to the full 360 degrees (via the /CYCEXPAND command), you can view a BC on the sector on which it is applied.
Issue BC-listing commands FLIST, DLIST, and SFLIST to list non-cyclically symmetric BCs. The list indicates the value of the BC and the sector on which it is applied.
During preprocessing, all tabular BC listings and plots referencing SECTOR will list the table names only.
During solution or postprocessing, all tabular BC listings and plots referencing SECTOR will list the values per sector as they would be applied when solving (SOLVE).
You can use graphical picking via the GUI to apply non-cyclically symmetric BCs on any sector. The graphical picking option is available after expanding the cyclic model (/CYCEXPAND). Applicable BCs are:
BCs applied by graphical picking ignore the current CYCOPT,LDSECT setting when cyclic expansion (/CYCEXPAND) is active. When cyclic expansion is not active, BCs are applied to the sector specified by CYCOPT,LDSECT (or all sectors if CYCOPT,LDSECT,ALL).
The mathematical characteristics of a cyclic symmetry solution require that displacement BCs (D, DK, DL, DA) apply to all sectors.