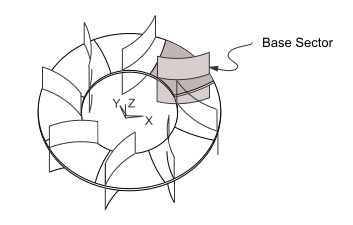
A cyclic symmetry analysis requires that you model a single sector, called the base sector. A proper base sector represents one part of a pattern that, if repeated N times in cylindrical coordinate space, yields the complete model, as shown:
A base sector model that is cyclically symmetric can be defined in any global or user-defined cylindrical coordinate system. (For information about creating a model, see the Modeling and Meshing Guide.)
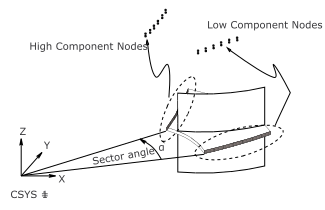
The angle α (in degrees) spanned by the base sector should be such that Nα = 360, where N is an integer. The base sector can consist of meshed or unmeshed geometry. The program allows user-defined coupling and constraint equations (including those created by MPC contact) only on nodes that are not on the low or high edges of the cyclic sector. (For more information about the cyclic sector's low and high edges, see Edge Component Pairs.)
If meshed, the base sector may have matching (as shown in Figure 2.2: Base Sector Definition) or unmatched lower and higher angle edges. Matching means that corresponding nodes exist on each edge, offset geometrically by the sector angle α. The edges may be of any shape and need not be "flat" in cylindrical coordinate space. For more information, see Identical vs. Dissimilar Edge Node Patterns.
If mistuning is to be included in a harmonic analysis (see Mode-Superposition Harmonic Cyclic Symmetry Analysis), the blade must be meshed such that the blade elements and the node interface separating the blade from the disk or the platform are readily separable. This can be accomplished by either carefully crafting a mesh (if a brick mesh) or by slicing the geometry before meshing (especially for a tet mesh). Note that the interface can exist at a location other than the blade-disk or blade-platform interface, for example, just above the fillet.