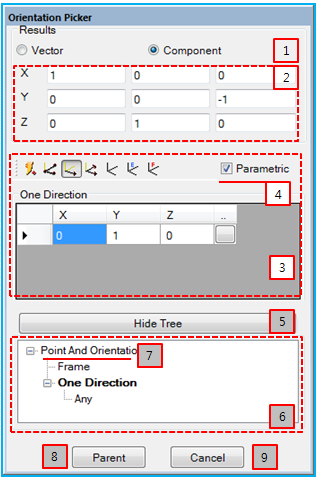
The Orientation Picker is used to get the orientation of constraints, forces and various other entities that require an orientation by using a geometry, design frame, and so on. The Orientation Picker has various functions to get the orientation on the screen easily as shown in the figure and table below.
Figure 1.81: Description of Orientation Picker properties
| Property | Description |
| 1. Result | Select either Vector or Component to determine the display format for orientations. Refer to the Point Picker for more information. |
| 2. Orientation | Show the orientation matrix or enter direction vectors for each component of the orientation matrix. |
| 3. Filter | Set a Filter for the orientation picker. |
| 4. Parametric | Create a parametric relationship between the resultant directions and the picking object. If the parametric option is selected, the resultant directions will be rotated when the picking object is rotated. The parametric option is only available for some filters, such as Three Points, One Direction, Two Directions, Three Directions and Frame. |
| 5. Hide Tree | Hide the history tree. |
| 6. History Tree | Show the picker history, which contains the filters and picked objects used, and allows access to the filters listed. This is useful when a picker has multi-step modeling depth and you change orientation during the modeling process. |
| 7. Operation | Access filters and objects in multi-step modeling. |
| 8. OK/Parent | Return to a previous modeling step and apply the resultant orientation. When on the first modeling step, this closes the orientation picker. |
| 9. Cancel | Return to the previous modeling step without applying the resultant orientation. When on the first modeling step, this closes the orientation picker. |
The Orientation Picker has various filters allowing selection of only a specific kind of object. The functionality of these filters is explained below.
Figure 1.82: Orientation Picker filters
| Filter | Symbol | Description |
| Any |
 | Orientation is determined by the selected Marker or Design Frame. |
| Three Points |
 |
Orientation is determined by the selected three points. X, Y and Z are unit vectors constructing an axis of orientation matrix and can be calculated as follows. Z = (P2 - P1) / | P2 - P1| → X' = (P3- P1) / | P2 - P1| → Y = (Z×X') → X = (Y×Z) where P1, P2, and P3 are the position vectors of 1st, 2nd, and 3rd selected points, respectively. This can be referred to when using the MultiPointCenter filter for the point picker. |
| One Direction |
 |
Orientation is determined by the direction selected using the direction picker. X, Y and Z are unit vectors constructing an axis of orientation matrix and can be calculated as follows. Z = D1 / |D1| → Y = (Z×XG) → X = (Y×Z) where, D1, and XG are the selected direction vector and the x-axis of the inertia reference frame. |
| Two Directions |
 |
Orientation is determined by the selected pair of directions by using the direction picker. X, Y and Z are unit vectors constructing an axis of orientation matrix and can be calculated as follows. Z = D1 / |D1| → Y = (Z×D2/|D2|) → X = (Y×Z), where D1 and D2 are the 1st and 2nd selected direction vectors. |
| Frame |
 |
Orientation is determined by the selected Marker or Design Frame. It can be controlled by using the Euler angle (see below). The functionality is as follows.
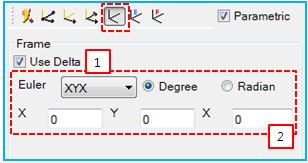
1. Use to input the delta for the relative rotational matrix. When the parametric option is selected, Use Delta becomes available. The orientation matrix of A can be determined as follows. A = A1 * A2 where A1 and A2 are the orientation matrix of the selected frame and the relative rotational matrix from the delta angle. |
| Euler Angle |
 |
Orientation is determined by the Euler angle which is entered directly. The Euler angle has 12 types, ZXZ, ZYZ, XZX and so on. For example, the orientation matrix from θ1, θ2 and θ3 in angle ZXZ is calculated as A. A= A1A2A3 |
| Fixed Angle |
 |
Orientation is determined by the Fixed angle which is entered directly. The Fixed angle has 12 types, ZXZ, ZYZ, XZX and so on. The axis of rotation is the global reference frame. For example, the orientation matrix from θ1, θ2 and θ3 in angle ZXZ is calculated as A. A= A3A2A1 |