VM76

VM76
Harmonic Response of a Guitar String

Overview

Reference:

R. D. Blevins, Formulas for Natural Frequency and Mode Shape, Van Nostrand Reinhold Co., New York, NY, 1979, pg. 90, tab. 7-1.

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Linear Perturbed Modal Analysis (ANTYPE = 2)

Linear Perturbed Harmonic Analysis (ANTYPE = 3)

Element Type(s):

3D Spar (or Truss) Elements (LINK180)

Input Listing:

vm76.dat

Test Case

A uniform stainless steel guitar string of length and diameter d is stretched between two rigid supports by a tensioning force F₁, which is required to tune the string to the E note of a C scale. The string is then struck near the quarter point with a force F₂. Determine the fundamental frequency, f₁. Also, show that only the odd-numbered frequencies produce a response at the midpoint of the string for this excitation.

Figure 106: Guitar String Problem Sketch

Material Properties

Geometric Properties

E = 190 x 10⁹ Pa

ρ = 7920 kg/m³

= 710 mm

c = 165 mm

d = 0.254 mm

F₁ = 84 N

F₂ = 1 N

Analysis Assumptions and Modeling Notes

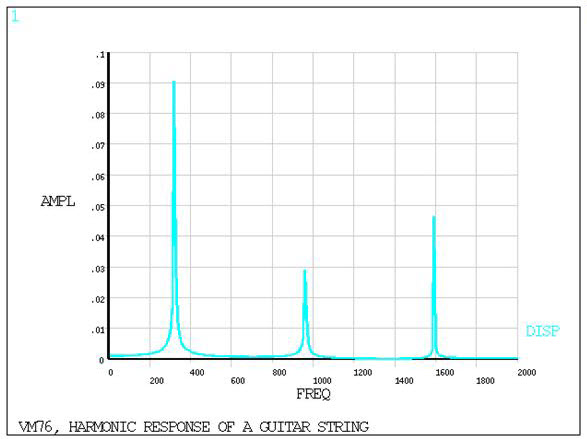
Enough elements are selected so that the model can be used to adequately characterize the string dynamics. The stress stiffening capability of the element is used. Linear perturbed harmonic analysis determines the displacement response to the lateral force F₂. The harmonic response is displayed with the time-history postprocessor, POST26, to show the excitation of the odd-numbered frequencies at peak displacement amplitudes. Refer to Figure 107: String Midpoint Displacement Amplitude.

Results Comparison

		Target	Mechanical APDL	Ratio
Modal	f, Hz	322.2	322.3	1.000
POST26	f₁, (322.2 Hz)	Response	Response, 320 < f < 328	-
	f₂, (644.4 Hz)	No Response	No Response	-
	f₃, (966.6 Hz)	Response	Response, 968 < f < 976	-
	f₄, (1288.8 Hz)	No Response	No Response	-
	f₅, (1611.0 Hz)	Response	Response,1624 < f < 1632	-
	f₆, (1933.2 Hz)	No Response	No Response	-

Figure 107: String Midpoint Displacement Amplitude