VM-WB-MECH-016

VM-WB-MECH-016
Fatigue Tool with Non-Proportional Loading for Normal Stress

Overview

Reference:	Any basic Machine Design book
Solver(s):	Ansys Mechanical
Analysis Type(s):	Fatigue Analysis
Element Type(s):	Solid

Test Case

A bar of rectangular cross section has the following loading scenarios.

Scenario 1: One of the end faces is fixed and a force is applied on the opposite face as shown below in Figure 16: Scenario 1.
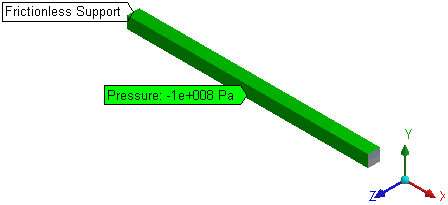
Scenario 2: Frictionless support is applied to all the faces of the three standard planes (faces not seen in Figure 17: Scenario 2) and a pressure load is applied on the opposite faces in positive y- and z-directions.

Find the life, damage, and safety factor for the normal stresses in the x, y, and z directions for non-proportional fatigue using the Soderberg theory. Use a design life of 1e6 cycles, a fatigue strength factor or 1, a scale factor of 1, and 1 for coefficients of both the environments under Solution Combination.

Figure 16: Scenario 1

Figure 17: Scenario 2

Material Properties
E = 2e11 Pa
ν = 0.3
Ultimate Tensile Strength = 4.6e8 Pa
Yield Tensile Strength = 3.5e8 Pa
Endurance Strength = 2.2998e6 Pa
Number of Cycles	Alternating Stress (Pa)
1000	4.6e8
1e6	2.2998e6

Geometric Properties

Bar: 20 m x 1 m x 1m

Loading

Scenario 1: Force = 2e6 N (y-direction)

Scenario 2: Pressure = -1e8 Pa

Analysis

Non-proportional fatigue uses the corresponding results from the two scenarios as the maximum and minimum stresses for fatigue calculations. The fatigue calculations use standard formulae for the Soderberg theory.

Results Comparison

Results		Target	Mechanical	Error (%)
Stress Component - Component X	Life	3335.1049	3329.9	-0.156
	Damage	299.8406	300.31	0.157
	Safety Factor	0.019	0.019025	0.132
Stress Component - Component Y	Life	14765.7874	14653	-0.764
	Damage	67.724	68.247	0.772
	Safety Factor	0.04569	0.045378	-0.683
Stress Component - Component Z	Life	14765.7874	14766	0.001
	Damage	67.724	67.725	0.001
	Safety Factor	0.04569	0.045696	0.013