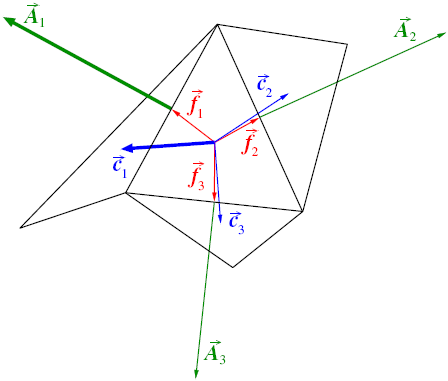
The range for orthogonal quality is 0-1, where a value of 0 is worst and a value of 1 is best.
The orthogonal quality for cells is computed using the face normal vector,
for each face, the vector from the cell centroid to the
centroid of each of the adjacent cells,
; and the vector from the cell centroid to each of the faces,
. Figure 52: Vectors Used to Compute Orthogonal Quality for a Cell illustrates the
vectors used to determine the orthogonal quality for a cell.
For each face, the cosines of the angle between and
, and between
and
, are calculated. The smallest calculated cosine value is the
orthogonality of the cell. Finally, Orthogonal Quality
depends on cell type:
For tetrahedral, prism, and pyramid cells, the Orthogonal Quality is the minimum of the orthogonality and (1 - cell skewness).
For hexahedral and polyhedral cells, the Orthogonal Quality is the same as the orthogonality.
Note:
When the cell is located on the boundary, the vector
across the boundary face is ignored during the quality computation.
When the cell is separated from the adjacent cell by an internal wall (a baffle), the vector
across the internal boundary face is ignored during the quality computation.
When the adjacent cells share a parent-child relation, the vector
is the vector from the cell centroid to the centroid of the child face while the vector
is the vector from the cell centroid to the centroid of the adjacent child cell sharing the child face.
Orthogonal quality in the Meshing application is equivalent to Inverse Orthogonal Quality in Ansys Fluent Meshing, except that the scale is reversed:
Inverse Orthogonal Quality = 1 – Orthogonal Quality
The orthogonal quality values may not correspond exactly with the inverse orthogonal quality values in Ansys Fluent because the computation depends on boundary conditions on internal surfaces (WALL vs. INTERIOR/INTERNAL/FAN/RADIATOR/POROUS-JUMP). Ansys Fluent may return different results which reflect the modified mesh topology on which CFD simulations are performed. The Tetrahedrons assembly algorithm uses only traditional element types.
For more information about Inverse Orthogonal Quality, see Quality Measure.
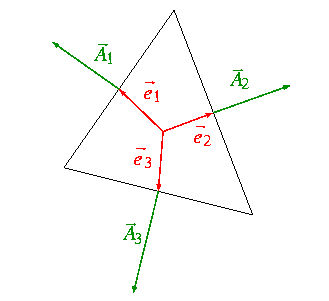
In a similar way, orthogonal quality for faces is computed as the smallest
cosine of the angle between the edge normal vector, for each edge and the vector from the face centroid to the
centroid of each edge,
. Figure 53: Vectors Used to Compute Orthogonal Quality for a Face illustrates the vectors
used to determine the orthogonal quality for a face.