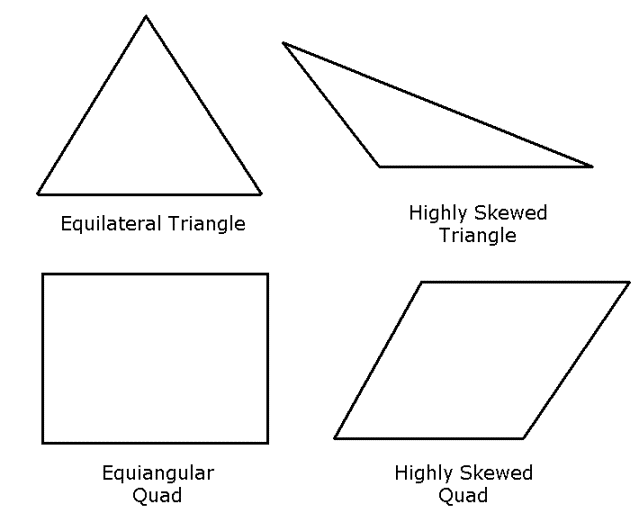
Skewness is one of the primary quality measures for a mesh. Skewness determines how close to ideal (equilateral or equiangular) a face or cell is (see Figure 51: Ideal and Skewed Triangles and Quadrilaterals).
The following table lists the range of skewness values and the corresponding cell quality.
| Value of Skewness | Cell Quality |
|---|---|
| 1 | degenerate |
| 0.9 — <1 | bad (sliver) |
| 0.75 — 0.9 | poor |
| 0.5 — 0.75 | fair |
| 0.25 — 0.5 | good |
| >0 — 0.25 | excellent |
| 0 | equilateral |
According to the definition of skewness, a value of 0 indicates an equilateral cell (best) and a value of 1 indicates a completely degenerate cell (worst). Degenerate cells (slivers) are characterized by nodes that are nearly coplanar (colinear in 2D).
Highly skewed faces and cells are unacceptable because the equations being solved assume that the cells are relatively equilateral/equiangular.
Two methods for measuring skewness are:
Based on the equilateral volume (applies only to triangles and tetrahedra).
Based on the deviation from a normalized equilateral angle. This method applies to all cell and face shapes, including pyramids and prisms.
Equilateral-Volume-Based Skewness
In the equilateral volume deviation method, skewness is defined as
where, the optimal cell size is the size of an equilateral cell with the same circumradius.
Quality meshes have a skewness value of approximately 0.1 for 2D and 0.4 for 3D. The table above provides a general guide to the relationship between cell skewness and quality.
In 2D, all cells should be good or better. The presence of cells that are fair or worse indicates poor boundary node placement. You should try to improve your boundary mesh as much as possible, because the quality of the overall mesh can be no better than that of the boundary mesh.
In 3D, most cells should be good or better, but a small percentage will generally be in the fair range and there are usually even a few poor cells.
Note: The Equilateral-Volume-Based Skewness quality metric applies to any mesh element that includes a triangular face. For triangular and tetrahedral elements, all faces of which are strictly triangular, the Equilateral-Volume-Based Skewness metric applies directly. For wedge or pyramidal elements, which include combinations of triangular and quadrilateral faces, the Meshing application computes both Equilateral-Volume-Based Skewness metrics (for the triangular faces) and Normalized Equiangular Skewness metrics (for the quadrilateral faces and 3-D element, itself) and reports the maximum computed metric as the element skewness. As a result, Equilateral-Volume-Based Skewness metrics reported for meshes that contain wedge and/or pyramidal elements may include skewness values attributable to Normalized Equiangular Skewness computations.
Normalized Equiangular Skewness
In the normalized angle deviation method, skewness is defined (in general) as
where
θmax = largest angle in the face or cell
θmin = smallest angle in the face or cell
θe = angle for an equiangular face/cell (60 for a triangle, 90 for a square)
For a pyramid, the cell skewness will be the maximum skewness computed for any face. An ideal pyramid (skewness = 0) is one in which the 4 triangular faces are equilateral (and equiangular) and the quadrilateral base face is a square. The guidelines in the table above apply to the normalized equiangular skewness as well.