An Internal Combustion Engine (IC HCCI) model simulates a combustion cylinder in an internal combustion (IC) engine under auto-ignition conditions, most relevant to the study of fuel auto-ignition behavior, engine knock, and homogeneous charge compression ignition (HCCI) engines. Heywood [59] provides equations that describe the volume (to first order) as a function of time, based on engine parameters, including compression ratio, crank radius, connecting rod length, speed of revolution of the crank arm, and the clearance or displaced volume. These equations are described briefly below. The engine parameters are specified by the user directly in the Ansys Chemkin Interface for the Internal Combustion HCCI Engine Reactor Model.

Figure 8.6: Schematic of an engine cylinder

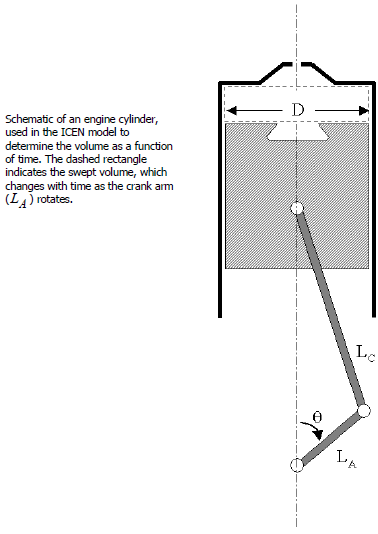
For the time-dependence of the engine cylinder volume, consider the diagram in Figure 8.6: Schematic of an engine cylinder . The connecting rod length is given by , while the crank arm radius is given by . The volume swept by the piston (cross-hatched area) is represented by the dashed rectangle above the piston. The clearance volume is represented by the open areas above and below the swept volume. The maximum swept or displaced volume is given by:

(8–42)

where is the cylinder bore diameter as shown in Figure 8.6: Schematic of an engine cylinder . The engine compression ratio is defined as the ratio of the maximum total volume to the clearance volume,

(8–43)

Note that in some cases it is only necessary to define the compression ratio, and it is not strictly necessary to define the clearance volume, since it is only used to scale the calculated volume. However, if the user is interested in performing post-analyses for engine efficiency, for example, or in the case that the IC HCCI Engine heat transfer coefficient correlation is used, the clearance volume should be specified with a physical value. By default, a value of 1.0 is assumed. The other parameter required for the IC HCCI Engine problem is , the ratio of the connecting rod length to the crank-arm radius :

(8–44)

Finally, the user must specify the rotation rate of the crank arm, where

(8–45)

With these definitions, one can derive the relationship between the total volume available for combustion in the cylinder as a function of time, scaled by the clearance volume: [59]

(8–46)

while the time derivative of the volume is:

(8–47)

Equation 8–42 through Equation 8–47 ) provide the volume and volume-derivative functions of time, which allows solution of the general equations for species and energy conservation discussed in General Equations .