VM317
VM317
Multistage Cyclic Modal Analysis of a Hollow Cylinder
Overview
| Reference: | Cammalleri, M. & Costanza, A. (2016). A closed-form solution for natural frequencies of thin-walled cylinders with clamped edges. International Journal of Mechanical Sciences, (110), 116-126. |
| Analysis Type(s): | Modal Analysis (ANTYPE = 2) Multistage Cyclic Analysis |
| Element Type(s): |
Structural Shell Elements (SHELL181) |
| Input Listing: |
vm317.dat
VM317 requires supplemental .cdb input files which are too long to include full input listings. These files must be downloaded and placed in your working directory for the test case to run properly. Additionally, the geometry and mesh should be regenerated. Download link: MAPDL Test Case Files for 2024 R2 vm317-1.cdb vm317-2.cdb |
Test Case
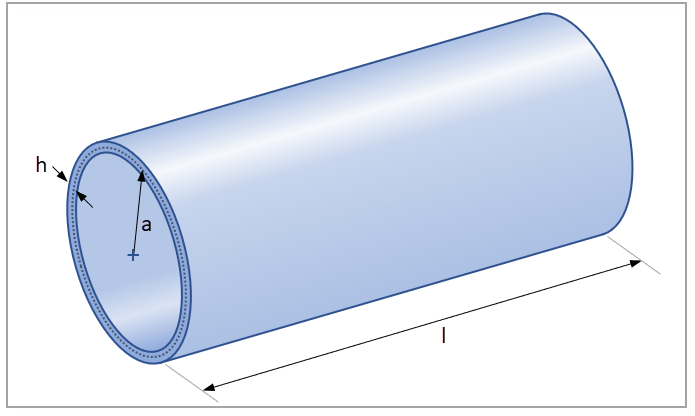
A thin-walled cylinder with length l, wall thickness h, and radius a (to the center line of the thin wall as shown below) is constrained with clamped-clamped boundary conditions. There are no loads since the natural frequencies are to be determined.
The parameters are defined in the following table.
| Material Properties | Geometric Properties | Loading |
|---|---|---|
|
E = 30E6 psi ρ = 0.283 lb/in3 ν = 0.3 | a = 3 in l = 12 in h = 0.01 in |
No loads |
Analysis Assumptions and Modeling Notes
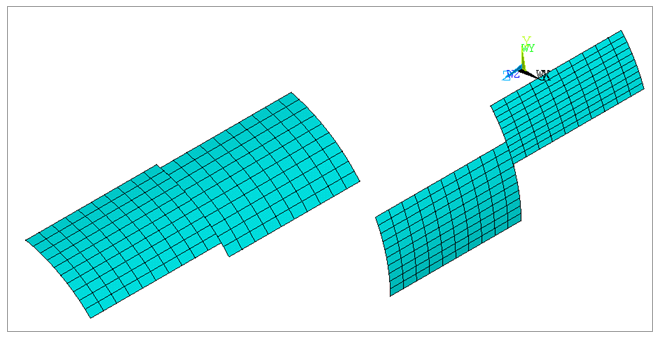
To model the thin-walled hollow cylinder, four cyclic stages are created as shown in the figure below. Each physical stage part is meshed separately using SHELL181 elements. Stages one through four have sector counts of 18, 13, 10, and 11, respectively. Each stage has a different starting angle. The stage objects are created using the MSOPT command, and cyclic constraints are applied to each stage using the CECYCMS command (see the Multistage Cyclic Symmetry Analysis Guide for details). Interstage constraints are applied using the CEIMS command. The modal solution is then obtained. The multistage stage generation and solution were for both harmonic index 4 and harmonic index 5.
Figure 581: Multistage cyclic stages with mesh
Results Comparison
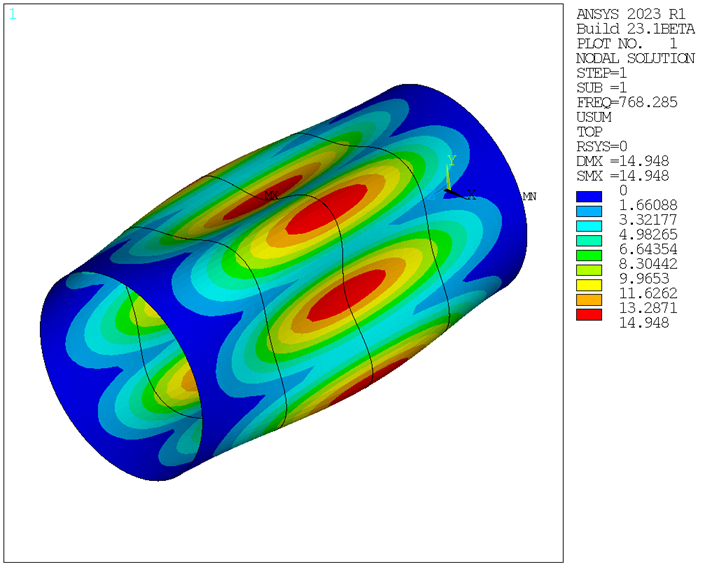
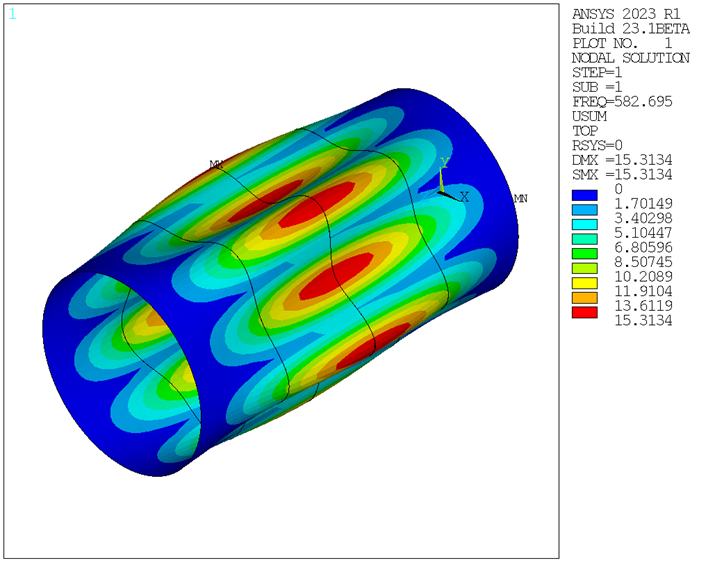
The natural frequencies are obtained from a full 360° FEA of the cylinder as well as from the multistage FEA. The frequencies are compared with the reference as seen in the results table below. It is noted that Cammalleri et al. saw similar differences between the analytical results and FEA. The value of M is the number of longitudinal half-waves, and the value of n is the number of circumferential waves which can be viewed as nodal diameters. The mode shapes are plotted (shown in the figures below) to verify they match with the reference.
| Comparison of Natural frequencies | |||||
|
n (# of nodal diameters) |
Target |
Mechanical APDL (Multistage) |
Ratio (Multistage) |
Mechanical APDL (Full 360°) |
Ratio (Full 360°) |
| 4 | 772 | 768.29 | 0.995 | 767.05 | 0.994 |
| 5 | 564 | 582.70 | 1.033 | 580.17 | 1.029 |