VM316
VM316
J-integral for a Middle-Crack Tension Specimen Under Elastic-Plastic
Deformation
Overview
| Reference: | Anderson, T. L. (2005). The EPRI J-estimation procedure. Fracture Mechanics: Fundamentals and Applications (3rd ed., pp. 398-444). CRC press. |
| Analysis Type(s): | Static Analysis (ANTYPE = 0) |
| Element Type(s): |
2D 8-Node Structural Solid (PLANE183) |
| Input Listing: |
VM316 requires a supplemental .cdb input file which is too long to include full input listings. This file must be downloaded and placed in your working directory for the test case to run properly. Additionally, the geometry and mesh should be regenerated. Download link: MAPDL Test Case Files for 2024 R2 vm316-1.cdb vm316-2.cdb |
Test Case
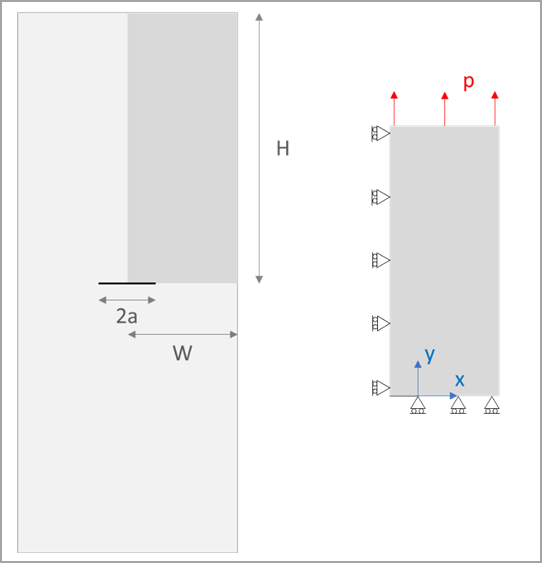
The problem analyzes a rectangular plate with a center crack subjected to uniform tension loading. The load causes elastic-plastic deformation in the model. Two analyses are performed, one with plane stress and the other with plane strain conditions. The J-integral result in each case is compared with the corresponding reference result based on the EPRI J-estimation method.
| Material Properties | Geometric Properties | Loading | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
Young's modulus:
Poisson's ratio:
Ramberg-Osgood parameters:
|
Crack size:
Width:
Height:
|
Traction: p = P/(2W) where P = 22500 N/mm is total force load on full specimen |
Analysis Assumptions and Modeling Notes
The problem is analyzed using 2D mesh based on PLANE183. Only one quarter of the plate is modeled due to symmetry. The symmetry boundary conditions are applied to the uncracked ligament (along y = 0) and to the vertical symmetry line (along x = –a). A uniform tensile traction is applied to the top edge of the plate using the SF command. A multilinear isotropic hardening (MISO) plasticity model is used to approximate the equivalent Ramberg-Osgood material model. The J-integral for the crack tip node is computed using CINT commands. The reference result based on the EPRI J-estimation is evaluated as follows.
(316–1) |
The elastic part is equal to elastic energy release rate G and is calculated as:
(316–2) |
The plastic part is calculated using the tabulated data published by EPRI (tables 9A.10 and
9A.11 in the reference).