Overview

Test Case

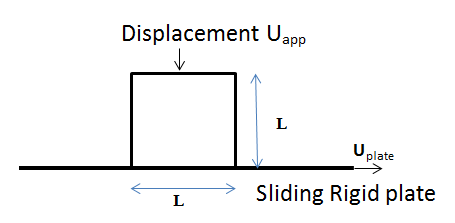
Wear analysis is performed on a block with length L in contact with a rigid plate using a frictionless standard contact pair. In the first load step, a displacement load is applied on one face of the block to compress the block onto the rigid plate. In the second load step, displacement is applied on the rigid plate to make it slide, resulting in wear of the block. The contact pressure and amount of wear on the block is computed and compared against the analytical solution.

Figure 497: Problem Schematic

Analysis Assumptions and Modeling Notes

The analysis is performed for two cases. In the first case, a 2D analysis is performed by modeling the block as a square plate with PLANE182 and CONTA172 elements using the Augmented Lagrangian contact algorithm. In the second case, a 3D analysis is performed by modeling the block as a cube using SOLID185 and CONTA174 elements using the Lagrange Multiplier algorithm.

Nonlinear static analysis with auto time stepping (AUTOTS) is performed with two load steps. The Archard wear model is defined using TB,WEAR. There is no wear in the first load step where the block is compressed against the rigid plate. The wear starts in the block during the second load step where the rigid plate is made to slide along the block.

As the block wears, more and more of the applied displacement is accommodated by the wear and hence the stress and contact pressure decreases with time. This results in decrease in the wear rate over time as well. The contact pressure (P) and accumulated wear (w) are compared with the analytical solution.

The analytical solution is obtained with the following equations, assuming a 1D problem:

Strain (ε) is related to total wear (w) and displacement (u_app) by:

The stress (σ) is related to strain by elastic constitutive equations as:

The contact pressure (P) is equal to the stress because of equilibrium conditions.

The rate of wear () is related to contact pressure and sliding velocity (v) by:

Results Comparison