VM280

VM280
Conduction in a Doubly Insulated Pipe Carrying Steam

Overview

Reference:

Kothandaraman, C.P., Fundamentals of Heat and Mass Transfer, 2006, p. 35

Analysis Type(s):

Steady-State Thermal Analysis (ANTYPE=0)

Element Type(s):

3D 8-Node Thermal Solid Element (SOLID278)

3D 20-Node Thermal Solid Element (SOLID279)

3D 10-Node Thermal Solid Element (SOLID291)

Input Listing:

vm280.dat

Test Case

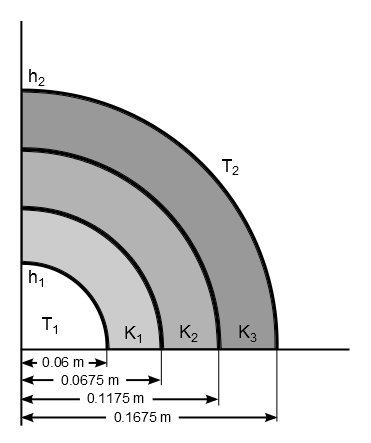
A pipe carrying steam at 230 °C has an internal diameter of 0.12 m and a thickness of 0.0075 m. The thermal conductivity of the pipe material, K₁, is 49 W/m⋅K and the convective heat transfer coefficient on the inside, h₁, is 85 W/m²K. The pipe is insulated by two layers of insulation, one with 0.05 m thickness with thermal conductivity, K₂, of 0.15 W/m⋅K and over it another layer with 0.05 m thickness with thermal conductivity, K₃, of 0.48 W/m⋅K. The outside is exposed to air at 35 °C with a convection coefficient, h₂, of 18 W/m²K. Determine the interface temperatures at locations x = 0.06 m, 0.0675 m, 0.1175 m, and 0.1675 m.

Figure 486: Pipe Carrying Steam with Insulation Layers Problem Sketch, One-Quarter Cross-Section

Material Properties	Geometric Properties	Loading
Thermal conductivity of pipe material, K₁ = 49 W/m⋅K Thermal conductivity of the 1^st insulation layer, K₂ = 0.15 W/m⋅K Thermal conductivity of the 2^nd insulation layer, K₃ = 0.48 W/m⋅K	Internal radius of the pipe = 0.06 m Thickness of the pipe = 0.0075 m Thickness of the 1^st insulation layer = 0.05 m Thickness of the 2^nd insulation layer = 0.05 m	Bulk temperature at pipe inner radius, T₁ = 230 °C Convective film coefficient at pipe inner radius, h₁ = 85 W/m²K Bulk temperature at the outside radius of the 2^nd insulation layer, T₂ = 35 °C Convective film coefficient at the outer radius of the 2^nd insulation layer, h₂ = 18 W/m²K

Material Properties

Geometric Properties

Thermal conductivity of pipe material, K₁ = 49 W/m⋅K

Thermal conductivity of the 1^st insulation layer, K₂ = 0.15 W/m⋅K

Thermal conductivity of the 2^nd insulation layer, K₃ = 0.48 W/m⋅K

Internal radius of the pipe = 0.06 m

Thickness of the pipe = 0.0075 m

Thickness of the 1^st insulation layer = 0.05 m

Thickness of the 2^nd insulation layer = 0.05 m

Bulk temperature at pipe inner radius, T₁ = 230 °C

Convective film coefficient at pipe inner radius, h₁ = 85 W/m²K

Bulk temperature at the outside radius of the 2^nd insulation layer, T₂ = 35 °C

Convective film coefficient at the outer radius of the 2^nd insulation layer, h₂ = 18 W/m²K

Analysis Assumptions and Modeling Notes

The problem is solved for three cases with a hollow cylinder using 3D 8-node thermal solid elements (SOLID278) for case 1, 3D 20-node thermal solid elements (SOLID279) for case 2, and with 3D 10-node thermal solid elements (SOLID291) for case 3.

The pipe and the insulation layers are modeled as separate volumes. The bulk temperatures and convective film coefficients at the inside radius of the pipe and the outside radius of the second insulation layer are defined via SFE,,,CONV for cases 1 and 2, and SF,,CONV for case 3.

A steady-state (static) thermal analysis is then performed to determine the interface temperature at various locations.

Results Comparison

	Target (°C)	Mechanical APDL (°C)	Ratio
Temperatures at the interface (SOLID278)
X = 0.06 m	222.300	222.236	1.000
X = 0.0675 m	222.200	222.141	1.000
X = 0.1175 m	77.040	76.207	0.989
X = 0.1675 m	48.030	50.068	1.042
Temperatures at the interface (SOLID279)
X = 0.06 m	222.300	222.258	1.000
X = 0.0675 m	222.200	222.163	1.000
X = 0.1175 m	77.040	76.508	0.993
X = 0.1675 m	48.030	50.133	1.044
Temperatures at the interface (SOLID291)
X = 0.06 m	222.300	222.298	1.000
X = 0.0675 m	222.200	222.203	1.000
X = 0.1175 m	77.040	77.042	1.000
X = 0.1675 m	48.030	48.028	1.000