VM281

VM281
Effect of Stress Stiffening and Spin Softening on a Rotating Plate

Overview

Reference:

Lawrence, C., Aiello, R. A., Ernst, M. A., McGee, O. G., “A NASTRAN Primer for the Analysis of Rotating Flexible Blades”, NASA Technical Memorandum 89861, 1987, p. 14

Analysis Type(s):

Static Analysis (ANTYPE = 0)

Linear Perturbation Modal Analysis (ANTYPE = 2)

Element Type(s):

4-Node Structural Shell Element (SHELL181)

8-Node Structural Solid Element (SOLID185)

Input Listing:

vm281.dat

Test Case

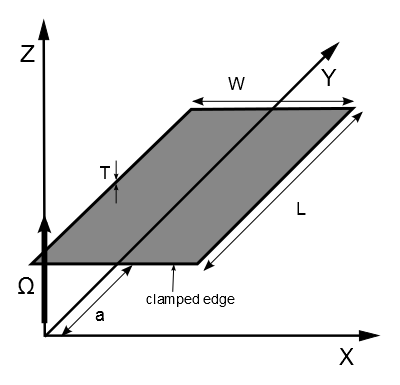
A steel plate, clamped on one edge and free on the other edges, is rotating about an offset axis. The first bending frequency is determined as a function of the rotational velocity. The analysis is done for two cases: rotation about the Z-axis (as shown in Figure 487: Problem Sketch of a Rotating Plate) and about the X-axis.

Figure 487: Problem Sketch of a Rotating Plate

Material Properties

Geometric Properties

Young’s Modulus, E = 2.0 x 10¹¹ Pa

Poisson’s Ratio, ν = 0.3

Density, ρ = 7850 kg/m³

Length, L = 0.1524 m

Width, W = 0.0508 m

Thickness, T = 0.00254 m

Offset^[a], a = 0.1 m

Rotational velocities, Ω = 0, 3200, 9600 RPM

^[a]The offset value is not specified in the reference. It was determined based on the frequency value at 9600 RPM along the Z-axis for the shell model.

Analysis Assumptions and Modeling Notes

The problem is solved for two cases. In the first case, the plate is modeled using 4-node structural shell elements (SHELL181). In the second case, the plate is modeled using 8-node structural solid elements (SOLID185). All degrees of freedom are constrained at the plane edge nearest the origin.

The rotational velocity is defined with CMOMEGA applied to all elements. The rotation is around the global X-axis (parallel to the plate width) or along the global Z-axis (perpendicular to the plate). For rotation about the X-axis, both the spin softening and stress stiffening affect the bending modes. For rotation about the Z-axis, the spin softening is negligible.

A nonlinear static analysis is performed, followed by a linear perturbation modal analysis to predict the bending modes using the Block-Lanczos eigensolver.

Results Comparison

		Bending Frequency (Hz)
SHELL181 Elements
Rotational Velocity Axis	Ω (RPM)	Target	Mechanical APDL	Ratio
none	0	90.000	90.831	0.991
X	3200	108.000	108.273	0.997
X	9600	195.000	195.139	0.999
Z	3200	121.000	120.686	1.003
Z	9600	250.000	252.359	0.991
SOLID185 Elements
Rotational Velocity Axis	Ω (RPM)	Target	Mechanical APDL	Ratio
none	0	90.000	90.875	0.990
X	3200	108.000	108.324	0.997
X	9600	195.000	195.237	0.999
Z	3200	121.000	120.725	1.002
Z	9600	250.000	252.419	0.990