VM248

VM248
Delamination Analysis of Double Cantilever Beam

Overview

Reference:

G. Alfano and M. A. CrisfieldFinite Element Interface Models for the Delamination Analysis of Laminated Composites: Mechanical and Computational Issues, International Journal for Numerical Methods in Engineering, Vol. 50, pp. 1701-1736 (2001).

Analysis Type(s):

Static analysis (ANTYPE = 0)

Element Type(s):

2D 4-Node Structural Solid Elements(PLANE182)

2D 4-Node Cohesive Zone Elements (INTER202)

2D 8-Node Structural Solid Elements(PLANE183)

2D 6-Node Cohesive Zone Elements (INTER203)

3D 8-Node Structural Solid Elements(SOLID185)

3D 8-Node Cohesive Zone Elements (INTER205)

2D 3-Node Surface-to-Surface Contact Elements (CONTA172)

3D 8-Node Surface-to-Surface Contact Elements (CONTA174)

2D Target Segment (TARGE169)

3D Target Segment (TARGE170)

Input Listing:

vm248.dat

Test Case

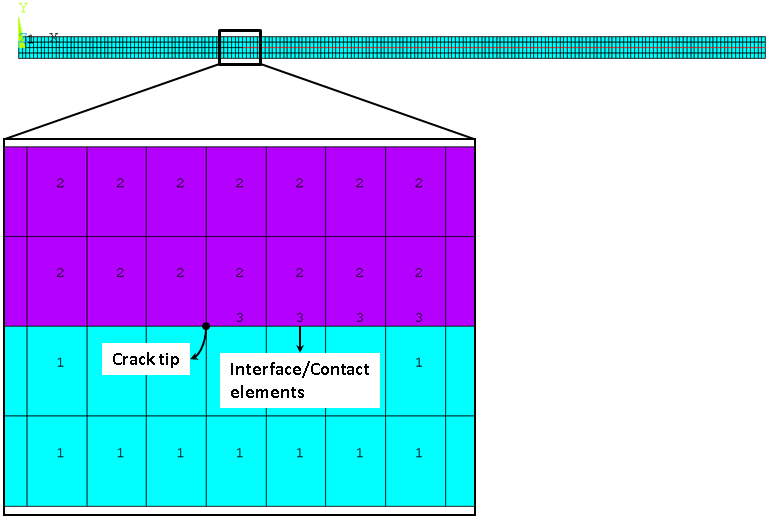
A double cantilever beam of length l, width w and height h with an initial crack of length a at the free end is subjected to a maximum vertical displacement U_max at top and bottom free end nodes. Determine the vertical reaction at point P based on the vertical displacement for the interface model.

Figure 421: Double Cantilever Beam Sketch

Figure 422: Representative Finite Element Model Using PLANE182 and Interface/Contact Elements

Material Properties

Geometric Properties

Composite

E₁₁ = 135.3 GPa

E₂₂ = 9.0 GPa

E₃₃ = 9.0 GPa

G₁₂ = 5.2 GPa

ν₁₂ = 0.24

ν₁₃ = 0.24

ν₂₃ = 0.46

L = 100 mm

a = 30 mm

h = 3 mm

w = 20 mm

U_max = 10 mm

Interface

C1 (maximum stress) = 25 MPa

C2 (normal separation) = 0.004 mm

C3 (shear separation) = 1000 mm

Analysis Assumptions and Modeling Notes

Static analysis is performed using regular meshes of 4 x 200 4-node INTER202 elements with PLANE182 elements, 2 x 200 6-node INTER203 elements with PLANE183 elements, 2 x 200 8-node INTER205 elements with SOLID185 elements, 4 x 200 2-node CONTA172 elements with PLANE182 elements, 2 x 200 3-node CONTA172 elements with PLANE183 elements, and 2 x 200 4-node CONTA174 elements with SOLID185 elements. In the 3D model, all the UZ degrees of freedom are constrained to make it behave like a 2D model. An imposed displacement of Uy = 10 mm acts at the top and bottom free nodes. Equivalent material constants of C1 = 25, C2 = 0.004 and C3 = 1000 are used for the interface material, as Mechanical APDL uses the exponential form of the cohesive zone model and the reference uses a bilinear constitutive model.

Results Comparison

INTER202
	Target	Mechanical APDL	Ratio
Max RFORCE and corresponding DISP:
RFORCE FY (N)	60.00	60.069	1.001
DISP UY(mm)	1.00	1.000	1.000
End RFORCE and corresponding DISP:
RFORCE FY (N)	24.00	24.294	1.012
DISP UY(mm)	10.00	10.00	1.00

INTER203
	Target	Mechanical APDL	Ratio
Max RFORCE and corresponding DISP:
RFORCE FY (N)	60.00	60.063	1.001
DISP UY(mm)	1.00	1.000	1.000
End RFORCE and corresponding DISP:
RFORCE FY (N)	24.00	24.299	1.012
DISP UY(mm)	10.00	10.00	1.00

INTER205
	Target	Mechanical APDL	Ratio
Max RFORCE and corresponding DISP:
RFORCE FY (N)	60.00	60.086	1.001
DISP UY(mm)	1.00	1.000	1.000
End RFORCE and corresponding DISP:
RFORCE FY (N)	24.00	24.281	1.012
DISP UY(mm)	10.00	10.00	1.00

CONTA172 (dropped midside nodes)
	Target	Mechanical APDL	Ratio
Max RFORCE and corresponding DISP:
RFORCE FY (N)	60.00	60.094	1.002
DISP UY(mm)	1.00	1.000	1.000
End RFORCE and corresponding DISP:
RFORCE FY (N)	24.00	24.296	1.012
DISP UY(mm)	10.00	10.00	1.00

CONTA172
	Target	Mechanical APDL	Ratio
Max RFORCE and corresponding DISP:
RFORCE FY (N)	60.00	60.088	1.001
DISP UY(mm)	1.00	1.000	1.000
End RFORCE and corresponding DISP:
RFORCE FY (N)	24.00	24.301	1.013
DISP UY(mm)	10.00	10.00	1.00

CONTA174 (dropped midside nodes)
	Target	Mechanical APDL	Ratio
Max RFORCE and corresponding DISP:
RFORCE FY (N)	60.00	60.110	1.002
DISP UY(mm)	1.00	1.000	1.000
End RFORCE and corresponding DISP:
RFORCE FY (N)	24.00	24.283	1.012
DISP UY(mm)	10.00	10.00	1.00