Overview

Test Case

Determine the view factors and radiative heat flux between two concentric spheres with radii R₁ and R₂, temperatures T₁ and T₂, and emissivity and .

Figure 382: Problem Sketch

Figure 383: Finite Element Model Using PLANE77 and SURF251 Elements

Figure 384: Finite Element Model Using SOLID90 and SURF252 Elements

Figure 385: Finite Element Model Using PLANE77, SOLID90, and SURF252 Elements

Figure 386: Finite Element Model Using PLANE77 and SURF252 Elements

Material Properties	Geometric Properties	Loading
Density, = 2700 kg/m3 Thermal conductivity, Kxx = 1.0 W/m˙K Specific heat, C = 1.0 J/K Stefan-Boltzmann constant, = 5.67 x 10-8 W/m2˙K4	R0 = 0.5 m R1 = 1 m R2 = 2 m R3 = 2.5 m	Emissivity on exterior of inside sphere, = 0.5 Emissivity on interior of outside sphere, = 0.4 Emissivity on all other surfaces, = 0 Temperature on interior of inside sphere, T1 = 100 K Temperature on exterior of outside sphere, T2 = 1000 K

Analysis Assumptions and Modeling Notes

The problem is solved for three cases.

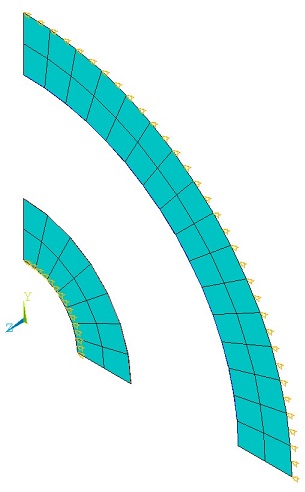
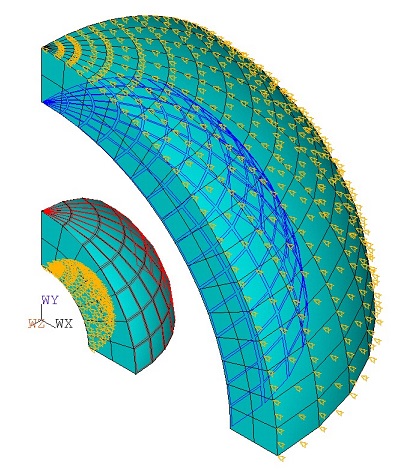
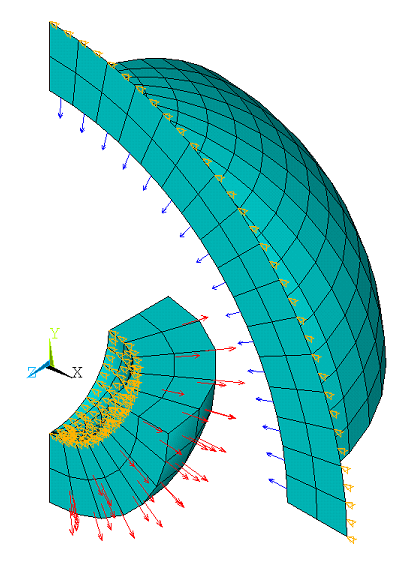
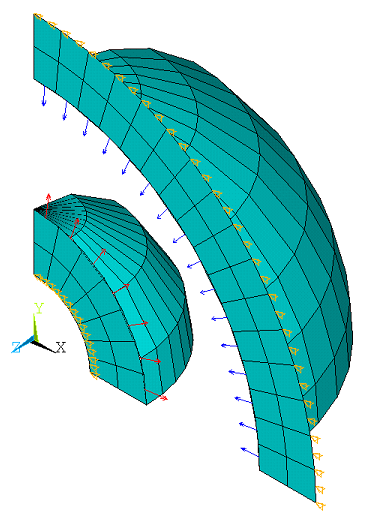
In the first case, the problem is solved by modeling the spheres using 2D axisymmetric thermal elements/radiosity surface elements PLANE77 and SURF251 and 3D thermal solid elements/radiosity surface elements SOLID90 and SURF252 with different radiation enclosure in the same preprocessing. The radiative symmetries for both the 2D and 3D models are specified using the RSYMM command. The radiosity surface elements are defined on the exterior of the inside sphere and the interior of the outside sphere using the RSURF command. Emissivity value sare defined on the facing surface using SF,,RDSF and temperatures T₁ and T₂ are specified at the non-facing surfaces, as shown in Figure 382: Problem Sketch,Figure 383: Finite Element Model Using PLANE77 and SURF251 Elements, and Figure 384: Finite Element Model Using SOLID90 and SURF252 Elements.

In the second case, the inner sphere is modeled using 3D solid thermal elements/radiosity elements SOLID90 and SURF252 and the external sphere is modeled using 2D axisymmetric thermal elements PLANE77 and 3D radiosity surface elements SURF252. The problem is solved with the same radiation enclosure. Axis = CENT is defined on the RSYMM command in the 2D case to circumferentially extrude the radiosity surface by SURF252 elements from 2D PLANE77 elements. The radiative symmetries, radiosity surface elements, emissivity values, and temperatures are defined as described for the first case and as shown in Figure 385: Finite Element Model Using PLANE77, SOLID90, and SURF252 Elements.

In the third case both the inner sphere and external sphere are modeled using 2D axisymmetric thermal elements PLANE77 and 3D radiosity surface elements SURF252. As mentioned in the second case, the SURF252 elements are generated from 2D PLANE77 elements using Axis = CENT on the RSYMM command. The radiative symmetries, radiosity surface elements, emissivity values, and temperatures are defined as described in the first case and as shown in Figure 386: Finite Element Model Using PLANE77 and SURF252 Elements.

View factors between two radiative sphere surfaces should satisfy basic rules of view factors:

The analytic solution for heat flux from the exterior of the inner sphere (equation 5.35 in the reference) is:

(230–1)

Because of conservation of energy, . The analytic value for heat flux from the interior of the outer sphere is

Results Comparison