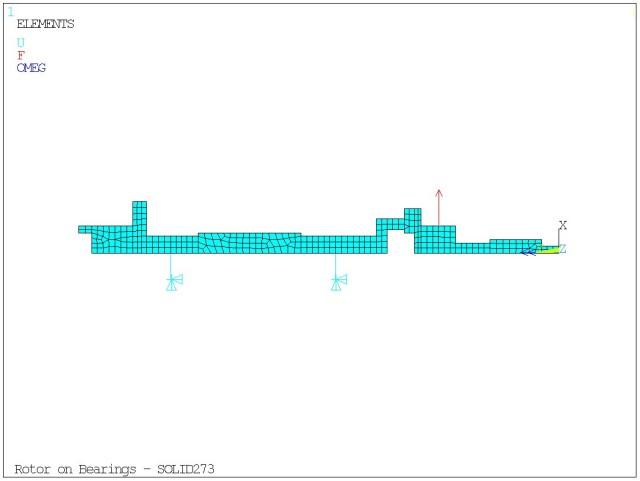
The model is depicted in Figure 7.3: Rotating Shaft. The shaft is rotating at 105000 RPM and is supported by two bearings. It is excited by an impulse along the X axis at a node situated in the right overhung part of the rotor.
The specifications for this model, including the geometry, and the stiffness characteristics for the identical bearings are found in VM247, "Campbell Diagrams and Critical Speeds Using Symmetric Bearings" in the Mechanical APDL Verification Manual.
/PREP7 MP,EX,1,2.078e+11 MP,DENS,1,7806 MP,NUXY,1,0.3 et,1,273,,3 !! 3 circumferential nodes nbdiam = 18 *dim,diam,array,nbdiam diam(1) = 1.02e-2 diam(2) = 2.04e-2 diam(3) = 1.52e-2 diam(4) = 4.06e-2 diam(5) = diam(4) diam(6) = 6.6e-2 diam(7) = diam(6) diam(8) = 5.08e-2 diam(9) = diam(8) diam(10) = 2.54e-2 diam(11) = diam(10) diam(12) = 3.04e-2 diam(13) = diam(12) diam(14) = 2.54e-2 diam(15) = diam(14) diam(16) = 7.62e-2 diam(17) = 4.06e-2 diam(18) = diam(17) k,1 k,2 ,diam(1)/2 k,3 ,diam(1)/2,1.27e-2 k,4 , ,1.27e-2 a,1,2,3,4 k,5 ,diam(2)/2,1.27e-2 k,6 ,diam(2)/2,5.08e-2 k,7 ,diam(3)/2,5.08e-2 k,8 , ,5.08e-2 a,4,3,5,6,7,8 k,9 ,diam(3)/2,7.62e-2 k,10, ,7.62e-2 a,8,7,9,10 k,11,diam(4)/2,7.62e-2 k,12,diam(4)/2,8.89e-2 k,13, ,8.89e-2 a,10,9,11,12,13 k,14,diam(5)/2,10.16e-2 k,15, ,10.16e-2 a,13,12,14,15 k,16,diam(6)/2,10.16e-2 k,17,diam(6)/2,10.67e-2 k,18,3.04e-2/2,10.67e-2 k,19, ,10.67e-2 a,15,14,16,17,18,19 k,20,diam(7)/2,11.43e-2 k,21,diam(8)/2,11.43e-2 k,22,3.56e-2/2,11.43e-2 k,23,3.04e-2/2,11.43e-2 a,18,17,20,21,22,23 k,24,diam(8)/2,12.7e-2 k,25,3.56e-2/2,12.7e-2 a,22,21,24,25 k,26, ,12.7e-2 k,27,diam(9)/2,13.46e-2 k,28,diam(10)/2,13.46e-2 k,29, ,13.46e-2 a,26,25,24,27,28,29 k,30,diam(10)/2,16.51e-2 k,31, ,16.51e-2 a,29,28,30,31 k,32,diam(11)/2,19.05e-2 k,33, ,19.05e-2 a,31,30,32,33 k,34,diam(12)/2,19.05e-2 k,35,diam(12)/2,22.86e-2 k,36, ,22.86e-2 a,33,32,34,35,36 k,37,diam(13)/2,26.67e-2 k,38,diam(14)/2,26.67e-2 k,39, ,26.67e-2 a,36,35,37,38,39 k,40,diam(14)/2,28.7e-2 k,41, ,28.7e-2 a,39,38,40,41 k,42,diam(15)/2,30.48e-2 k,43, ,30.48e-2 a,41,40,42,43 k,44,diam(16)/2,30.48e-2 k,45,diam(16)/2,31.5e-2 k,46,diam(17)/2,31.5e-2 k,47, ,31.5e-2 a,43,42,44,45,46,47 k,48,diam(17)/2,34.54e-2 k,49,3.04e-2/2,34.54e-2 k,50, ,34.54e-2 a,47,46,48,49,50 k,51,diam(18)/2,35.5e-2 k,52,3.04e-2/2,35.5e-2 a,49,48,51,52 esize,0.5e-2 amesh,all sect,1,axis !! symmetry axis along Y secd,1, 0,0,0, 0,1,0 naxi ! bearings et,3,combin14 keyopt,3,2,1 et,4,combin14 keyopt,4,2,2 et,5,combin14 keyopt,5,2,3 r,3,4.378e+7 visu = -0.02 !! visualization of bearing n,10000,visu,16.51e-2 n,10001,visu,28.7e-2 type,3 real,3 e,node(0,16.51e-2,0),10000 e,node(0,28.7e-2,0),10001 type,4 real,3 e,node(0,16.51e-2,0),10000 e,node(0,28.7e-2,0),10001 type,5 real,3 e,node(0,16.51e-2,0),10000 e,node(0,28.7e-2,0),10001 d,10000,all d,10001,all fini ! *** modal analysis in rotation pi = acos(-1) spin = 105000*pi/30 /solu antype,modal modopt,qrdamp,10,1.0 coriolis,on,,,on betad,1.e-5 omega,,spin mxpand,10,,,yes solve fini ! *** mode-superposition transient analysis dt = 1.0e-04 nodF = node(0.20300E-01,0.88900E-01,0) /solu antype,transient trnopt,msup,10 deltim,dt kbc,0 outres,all,none outres,nsol,all outres,rsol,all f,nodF,FX,0 time,2*dt solve f,nodF,FX,1.e+3 time,10*dt solve f,nodF,FX,0 time,100*dt solve fini ! *** expansion pass /solu expass,on numexp,all solve fini ! *** generate bearing reaction forces plot /post26 rforce,2,10000,F,X,fxRightBearing rforce,3,10000,F,Z,fzRightBearing rforce,4,10001,F,X,fxLeftBearing rforce,5,10001,F,Z,fzLeftBearing /show,JPEG plvar,2,3,4,5 EXTREME,2,5,1 /show,CLOSE
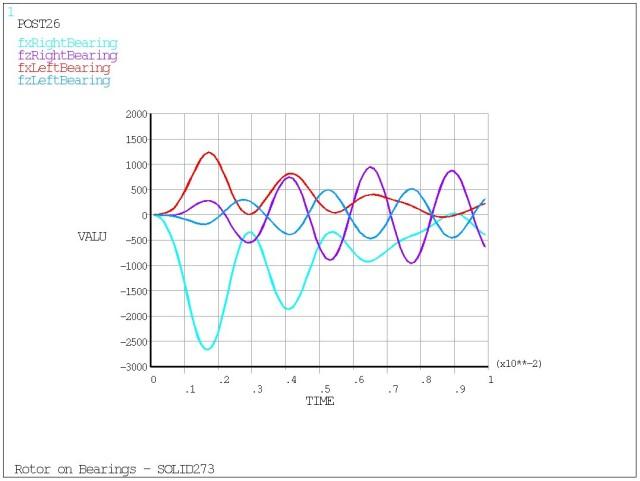
The plot of Bearing Reaction Forces vs. Time is shown in Figure 7.4: Rotating Shaft Output.