The flow of water or other liquid through porous media (such as soils) occurs when a difference in the water level exists, causing fluid pressure. Darcy's law defines porous media flow:

(4–86)

where:

= flow flux (Units: Length / Time)

= relative permeability

= permeability

= degree of fluid saturation

= specific weight of fluid

= pore pressure

= gradient operator (3D form shown)

= gravity load direction (not to be confused with gravity magnitude)

Porous media are multiphase materials containing pores. The void ratio is defined by:

where:

= void volume

= solid volume

Porosity is defined as:

where = total volume.

Porosity and void ratio are related by:

The balance equations assume small-strain theory. They are as follows:

 

4.12.2.1. Momentum-Balance Equation

The momentum-balance equation for a two-phase medium:

(4–87)

where:

= total stress tensor

= matrix differentiation operator (3D form shown)

= displacement

= bulk specific weight of porous media (defined as , where is the solid skeleton specific weight and is the porosity)

= bulk density of porous media

The bulk density of the porous media is entered via the MP,DENS or TB,DENS commands. When solid and fluid properties are defined (TB,PM,,,,SP or FP) and gravity magnitude is defined (TB,PM,,,,GRAV), bulk density is calculated as:

where is the magnitude of gravitational acceleration. A typical value is 9.8m/s^-2.

The specific weights of solid and pore fluid are defined via the porous media data table (TB,PM). The gravity load direction is defined via the specific weight load setting (SSOPT,SFSW).

 

4.12.2.2. Mass-Balance (Continuity) Equation for the Pore-Fluid Phase

The mass-balance (continuity) equation for the pore-fluid phase is:

(4–88)

where:

= volumetric strain

= compressibility parameter

= free strain

= temperature

The following topics for the mass-balance (continuity) equation are available:

• 4.12.2.2.1. Compressibility Parameter
• 4.12.2.2.2. Biot Coefficient
• 4.12.2.2.3. Effective Stress
• 4.12.2.2.4. Free-Strain Rate

 

4.12.2.2.1. Compressibility Parameter

The compressibility parameter is calculated from the Biot modulus (TB,PM,,,,BIOT) and partially saturated parameters:

For fully saturated flow the parameters take the following values:

When solid and fluid properties are defined (TB,PM,,,,SP or FP), the compressibility parameter is calculated using the solid skeleton and fluid modulus as:

(4–89)

where:

= bulk modulus of skeleton

= bulk modulus of fluid

In this case, the Biot modulus input via TB,PM,,,,BIOT is ignored.

 

4.12.2.2.2. Biot Coefficient

The Biot coefficient is input via the TB,PM,,,,BIOT command. However, if solid and fluid properties are defined (TB,PM,,,,SP/FP), the Biot coefficient is calculated as:

where:

= tangential bulk modulus

= material tangent stiffness (from solid skeleton material behavior)

 

4.12.2.2.3. Effective Stress

The constitutive behavior of the solid skeleton is based on effective stress principal that describes mechanical response of material. The solid part of the model is represented by the effective stress as:

(4–90)

where is the effective stress tensor. In general, the effective stress is a function of time, strain and other history-dependent solution variables, if any.

The effective stress causes all relevant deformation of the solid skeleton and is related to the elastic strain tensor via Hooke's law:

(4–91)

where:

= material elastic tangent stiffness

= elastic strain tensor

= plastic strain tensor

= thermal strain tensor

= initial strain tensor

= inelastic strains other than plasticity

 

4.12.2.2.4. Free-Strain Rate

The form of the free-strain-rate term depends on the thermal expansion coefficient (CTE) definitions:

• Form 1 – Only solid skeleton CTE defined:

  

  where:

  = instantaneous volumetric thermal expansion coefficient

  = solid skeleton instantaneous volumetric thermal expansion coefficient

  = linear instantaneous thermal expansion coefficients

  Defining the instantaneous solid skeleton CTEs

  The instantaneous thermal expansion coefficients are equal to the secant thermal expansion coefficients if there is no variation of the coefficients during solution (that is, if there is no temperature or other field-variable dependence). In that case, define the instantaneous solid skeleton CTEs via TB,CTE (secant CTE input). If the TB,CTE properties are made temperature- (or other field-variable-) dependent, the program uses the CTE values directly without accounting for conversion to instantaneous values. To account for temperature dependence of the instantaneous solid skeleton CTEs, define the solid skeleton CTEs via MP commands (MPTEMP and MPDATA,CTEX/Y/Z). In this case, the program uses the instantaneous CTE directly with respect to the mass balance (continuity) equation for the pore-fluid phase (Equation 4–88). For the momentum-balance equation of the porous medium (Equation 4–87), which uses the secant CTE, the program converts the instantaneous values to the secant values.

• Form 2 – Fluid CTE defined:

  

  where:

  = fluid-thermal-expansion coefficient (input via TB,CTE,,,,FLUID)

• Form 3 – User-defined free-strain rate:

  

  You can define the free-strain increment via the userfreestrain subroutine.

The free-strain rate term can behave in either of two ways depending on whether the temperature degree of freedom is enabled:

– Temperature degree of freedom disabled:

If the temperature history is defined (via BF or BFE, for example), the free-strain rate (any form) acts as a load. The user-defined free-strain feature (form 3) is available only if the temperature degree of freedom is disabled.

– Temperature degree of freedom enabled:

Available for forms 1 and 2 only, the temperature is solved as part of the coupled system of equations.

 

4.12.2.3. Heat-Transfer Equation

The heat-transfer equation is:

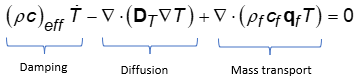(4–92)

where:

= thermal conductivity (Units: Mass * Length * Temperature-1 * Time-3)

= fluid density calculated as .

The form of depends on the TB table definition:

• Only TB ,THERM,,,,SPHT defined:

  

  where:

  = solid-skeleton specific heat

• TB ,THERM,,,,FLSPHT defined:

  

  where:

  = fluid specific heat

  = solid-skeleton density calculated as

 

4.12.2.3.1. Stability of Galerkin Formulation

The stability of the Galerkin formulation is measured in terms of the non-dimensional criteria called the element Peclet number, which calculates the ratio between the mass transport term and the diffusion term. The Peclet number is calculated in a similar manner to Equation 4–1 in the Thermal Analysis Guide, where the velocity vector is replaced by the fluid flow flux.

To ensure Galerkin formulation stability, the recommended Peclet number should be < 1.

The material properties for porous media analysis include solid skeleton and pore-fluid properties. Define material model constants for a porous medium (TB,PM).

The following material-property options (TBOPT) are available for defining porous media:

Define constants (Cn) via TBDATA (or TBPT, as applicable).

 

4.12.3.1. Permeability (TB,PM,,,,TBOPT = PERM)

The permeability properties can be isotropic, orthotropic or anisotropic. The full 3 x 3 permeability matrix is:

Define up to nine constants:

Isotropic permeability matrix -- Define only. (The and values are assumed to be . )

Orthotropic permeability matrix -- Enter three constants: , and . The program assigns values of zero to the off-diagonal permeability constants ().

Anisotropic permeability matrix -- If you define the first six constants (), the program makes the permeability matrix symmetric (that is, ).

General nonsymmetric anisotropic permeability matrix -- Define all nine constants.

Constant	Meaning	Units
C1		Length/Time
C2
C3
C4
C5
C6
C7
C8
C9

All defined constants are based on the element coordinate system. By default, the element coordinate system is the global coordinate system.

 

4.12.3.2. Biot Coefficient (TB,PM,,,, TBOPT = BIOT)

Define the Biot coefficient and Biot modulus.

If the Biot coefficient remains undefined, the program assigns a default value of 1. If the Biot modulus remains undefined, the porous media is assumed to be incompressible.

Constant	Meaning	Property	Units
C1		Biot coefficient	Dimensionless
C2		Biot modulus	Force/Length2

If solid property and/or fluid property is defined (TB,PM,,,,SP/FP), the Biot coefficient and Biot modulus are overwritten with values calculated as described in Porous Media Mechanics.

 

4.12.3.3. Solid Property (TB,PM,,,, TBOPT = SP)

Defining either of the available constants is optional:

• If the bulk modulus of the solid skeleton is not defined, the solid skeleton is assumed to be incompressible.

• If the specific weight of the solid skeleton is defined, the program considers it to be a body force.

Constant	Meaning	Property	Units
C1		Bulk modulus of solid skeleton	Force/Length2
C2		Specific weight of solid skeleton	Force/Length3

 

4.12.3.4. Fluid Property (TB,PM,,,, TBOPT = FP)

Defining any of the three available constants is optional:

• If the bulk modulus of the fluid is not defined, the fluid is assumed to be incompressible.

• If the specific weight of the fluid is defined, the program considers it to be a body-force load.

Constant	Meaning	Property	Units
C1		Bulk modulus of fluid	Force/Length2
C2		Specific weight of fluid	Force/Length3
C3		Porosity	Dimensionless

 

4.12.3.5. Degree of Saturation (TB,PM,,,, TBOPT = DSAT)

Define the degree of saturation as a function of pore pressure (TBPT). Pore-pressure values can be negative only (partially saturated flow), and the degree of saturation lies between 0 and 1. If undefined, the degree of saturation defaults to 1.

Constant	Meaning	Property	Units
C1		Pressure	Force/Length2
C2		Degree of fluid saturation	None

 

4.12.3.6. Relative Permeability (TB,PM,,,, TBOPT = RPER)

Define the relative permeability as a function of pore pressure (TBPT). Pore-pressure values can be negative only (partially saturated flow), and relative permeability lies between 0 and 1. If undefined, the relative permeability defaults to 1.

Constant	Meaning	Property	Units
C1		Pressure	Force/Length2
C2		Relative permeability	None

 

4.12.3.7. Gravity Magnitude (TB,PM,,,, TBOPT = GRAV)

Define the magnitude of gravity.

Constant	Meaning	Property	Units
C1		Gravity magnitude	Force/Length2

If solid and/or fluid properties are defined (TB,PM,,,,SP/FP) and gravity magnitude is defined (TB,PM,,,,GRAV), bulk density is calculated as described in Porous Media Mechanics.

If gravity magnitude is not defined, it is assumed to be 1.

Thermal conductivity (TBOPT = COND), solid-skeleton specific heat (TBOPT = SPHT), and fluid specific heat (TBOPT = FLSPHT) are defined via TB,THERM. For more information about defining thermal material properties, see Thermal Properties.

The solid-skeleton volumetric thermal-expansion coefficient is the sum of the linear thermal-expansion coefficients defined via TB,CTE (or MPTEMP and MPDATA,CTEX/Y/Z).

The fluid volumetric thermal expansion coefficient is directly defined via TB,CTE,,,,FLUID.

A soil-consolidation problem is typically a transient analysis (ANTYPE,SOIL or ANTYPE,TRANS). A transient analysis considers all rate (, , ) and acceleration () terms in the governing equations (Equation 4–87, Equation 4–88, and Equation 4–92).

In a geostatic analysis (ANTYPE,SOIL with SSOPT,GEOSTATIC), all transient terms (acceleration and rate) are ignored.

In a static analysis (ANTYPE,STAT), all acceleration terms are ignored; however, the program accounts for the following rate terms: volumetric strain rate (), pressure rate (), free-strain rate , and specific heat damping in the mass-balance and heat-transfer equations.

In a static analysis, applying fluid flow (FLOW) and heat flow (HEAT) (via the nodal-force command F) is not supported. If those are needed, use a transient analysis.

Soil embankments and dams are examples of semi-saturated porous media. Such structures are often characterized by a phreatic line (free water surface). The soil below the phreatic line is fully saturated, while the soil above is partially saturated. Partially saturated flow results in negative pore pressures. The presence of negative pore pressures is beneficial to the soil. It assures some cohesion in the soil, essential for maintaining its structural integrity.

Partially saturated porous media flow does not introduce any new degrees of freedom to coupled pore-pressure-thermal elements (CPTnnn); that is, pore pressure is still the extra degree of freedom in addition to the displacement degrees of freedom). Partially saturated behavior is modeled by introducing two new parameters, the degree of saturation and the relative permeability, both of which are functions of the negative pore pressure. The relationships can be defined in tabular form (TB,PM,,,,DSAT and TB,PM,,,,RPER, respectively).

CPT damping refers to Rayleigh damping, available for CPTnnn elements via the TB,SDAMP,,,,ALPD/BETD command.

For more information, see Example: Initial Degree of Saturation and Relative Permeability in the Advanced Analysis Guide.