The following examples are available:
This example problem shows how to perform a steady-state conduction current analysis.
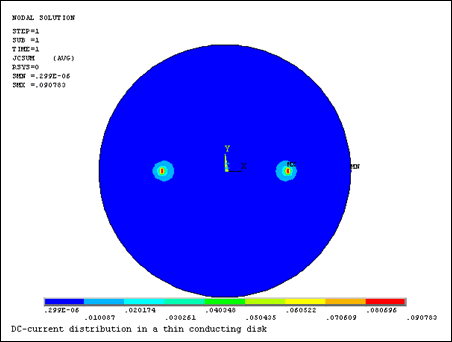
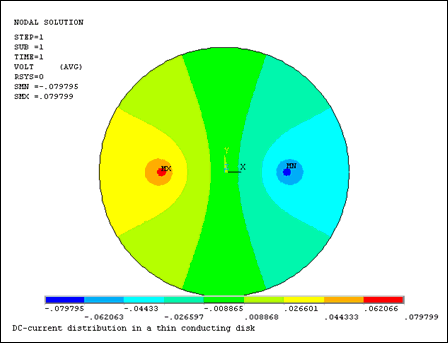
A current I is applied to a thin disk of radius r = a. As shown in the following figure, the current enters and leaves via point electrodes located at r = b, ϕ = 0 and r = b, ϕ = π. Find the potential and dc-current distributions in the disk.
The geometric and electrical parameters are:
| Radius a = 20 cm |
| Distance from the center to the point electrodes b = 10 cm |
| Applied Current I = 1 mA |
| Disk Resistivity ρ = 100 Ωm |
To obtain an accurate field distribution, the disc area is densely meshed with triangle-shaped PLANE230 electric elements. A VOLT degree of freedom constraint is applied to the center of the disk. Current loads are applied as concentrated nodal loads. A cylindrical coordinate system is used.
Table 12.19: Electric Potential at Points with Coordinates r = a and ϕ
| ϕ (degrees) | Electric Potential (V) | |
|---|---|---|
| Computed | Target [1 ] | |
| 0 | –.03501 | –.03497 |
| 10 | –.03399 | –.03392 |
| 20 | –.03124 | –.03110 |
| 30 | –.02708 | –.02716 |
| 40 | –.02269 | –.02271 |
| 50 | –.01814 | –.01810 |
| 60 | –.01360 | –.01349 |
| 70 | –.00880 | –.00894 |
| 80 | –.00438 | –.00445 |
| 90 | 0.0 | 0.0 |
The following figures display the potential and dc-current distributions in the disk.
You can perform this example steady-state analysis using the Mechanical APDL commands shown below. Text prefaced by an exclamation point (!) is a comment.
/batch,list /title, DC-current distribution in a thin conducting disk a=20.e-2 ! disk radius, m b=10.e-2 ! electrode distance from the center, m I=1.e-3 ! current, A rho=100 ! resistivity, Ohm*m /nopr /PREP7 ! Model and meshing et,1,PLANE230 ! electric element type mp,rsvx,1,rho ! resistivity cyl4,0,0,0,0,a,360 ! circular area esize,,64 msha,1,2D ! mesh with triangles amesh,1 ! Boundary conditions csys,1 ! cylindrical coordinate system d,node(0,0,0),volt,0 ! ground center node ! Nodal current loads f,node(b,0,0),amps,-I f,node(b,180,0),amps,I fini /solu antype,static ! steady-state current conduction solve fini /post1 plnsol,volt ! plot electric potential plnsol,jc,sum ! plot current density vector magnitude *dim,value,,10,2 *dim,coord,,10,2 *do,i,1,10 ! coordinates of solution point r=a $ phi=(i-1)*10 coord(i,1)=r coord(i,2)=phi ! Mechanical APDL solution value(i,1)=volt(node(a,(i-1)*10,0)) *enddo ! Analytical solution *vfill,value(1,2),data,-0.034969,-0.033923,-0.031098,-0.027163,-0.022709 *vfill,value(6,2),data,-0.018095,-0.013485,-0.008937,-0.004451,0. /com,---------------- VOLT SOLUTION ---------------- /com, /com, R | PHI | Mechanical APDL | TARGET /com, *vwrite,coord(1,1),coord(1,2),value(1,1),value(1,2), (1X,' ',F6.1,' ',F6.1,' ',F11.6,' ',F11.6) /com,------------------------------------------------- fini
This problem evaluates conductance between parallel plate electrodes. The objective is to calculate the self and mutual conductance coefficients between two parallel plate electrodes.
The model consists of two parallel plate electrodes, 3 m in length, with a gap of 2 m and a conductivity of 10. One electrode represents the ground, and 100 volts is applied to the other electrode. The target conductance is 15.
/title,Conductance between parallel plate electrodes using GMATRIX /com Input data /com sigma : conductivity /com g : gap between electrodes /com w : electrode width /com l : length /com /com Target /com /com G = sigma w l / g : conductance between parallel plate electrodes ! g=2 ! gap between electrodes w=3 ! electrode width l=1 ! length sigma=10 ! conductivity ! gt=sigma*w*l/g ! target conductance ! /prep7 et,1,230 mp,rsvx,1,1/sigma ! n,1,0,0 n,2,w,0 n,3,w,g n,4,0,g e,1,2,3,4 ! nsel,s,loc,y,g ! electrode cm,comp1,node d,all,volt,100 ! nsel,s,loc,y,0 ! ground cm,comp2,node d,all,volt,0 ! nsel,all ! gmatrix,1,'comp',2,0 ! compute conductance matrix gc=gmatrix(1,1,1) ! computed conductance finish
A time-harmonic voltage of amplitude Vo is applied to a barium titanate parallel plate capacitor with circular plates of radius a and dielectric thickness d. The dielectric has relative permittivity εr and loss tangent tanδ. Perform a harmonic analysis to determine the capacitor admittance (Y) in the frequency (f) range of 0 to 1 MHz, and find the dissipated power at 1 MHz.
The geometric and electrical parameters are:
| Radius a = 9 cm |
| Thickness d = 0.1 cm |
| Relative Permittivity εr = 1143 |
| Loss tangent tanδ = 0.0105 |
| Voltage amplitude Vo = 50 volts |
| Frequency f = 0 to 1 MHz |
The capacitor is modeled using the axisymmetric option of PLANE230 electric elements. Electrodes are defined by coupling VOLT degrees of freedom on the major surfaces of the capacitor. The bottom electrode is grounded, and a voltage load Vo is applied to the top electrode.
Electric admittance (Y) is calculated at ten frequencies between 0 and 1 MHz using the reaction current on the loaded electrode. Results are compared with target values obtained from the following analytical expression:
Y = 2πfC(tanδ+j)
where:
and j = imaginary unit.
Power dissipation at f = 1 MHz is calculated in /POST1 by summing up the Joule heat rates over the elements. The result is compared with the following analytical expression for the time-average power dissipated in the capacitor:
As shown in the following table, the Mechanical APDL electric admittance (Y) results agree with those from the analytical expression given above.
Table 12.20: Electric Admittance (Y)
| Frequency (MHz) | Admittance Amplitude (S) [1] |
|---|---|
| 0.0 | 0.1618 |
| 0.2 | 0.3236 |
| 0.3 | 0.4855 |
| 0.4 | 0.6473 |
| 0.5 | 0.8091 |
| 0.6 | 0.9709 |
| 0.7 | 1.1327 |
| 0.8 | 1.2945 |
| 0.9 | 1.4564 |
| 1.0 | 1.6182 |
The power dissipated at a frequency of 1 MHz is 21.2 watts.
You can perform this example harmonic analysis using the Mechanical APDL commands shown below. Text prefaced by an exclamation point (!) is a comment.
Besides commands to perform this analysis using the PLANE230 electric elements, this command listing includes the commands to do the same analysis using PLANE121 electrostatic elements.
/batch,list /title, Harmonic response of a lossy capacitor /com, /com, Problem parameters: a=9.e-2 ! radius, m d=0.1e-2 ! thickness, m epsr=1143 ! relative permittivity tand=0.0105 ! loss tangent Vo=50 ! voltage amplitude, V f1=0 ! begin frequency, Hz f2=1.e6 ! end frequency, Hz eps0=8.854e-12 ! free space permittivity, F/m Pi=acos(-1) C=epsr*eps0*Pi*a**2/d ! capacitance, F P2d=Pi*f2*Vo**2*C*tand ! power dissipation at freq. f2, watt /nopr /PREP7 et,1,PLANE230,,,1 ! axisymmetric electric element emunit,epzro,eps0 ! specify free-space permittivity mp,perx,1,epsr ! electric material properties mp,lsst,1,tand rect,,a,,d ! model and mesh esize,d/2 amesh,1 ! Boundary conditions and loads nsel,s,loc,y,0 cp,1,volt,all ! define bottom electrode *get,n_grd,node,0,num,min ! get master node on bottom electrode nsel,s,loc,y,d cp,2,volt,all ! top electrode *get,n_load,node,0,num,min ! get master node on top electrode nsel,all d,n_grd,volt,0 ! ground bottom electrode d,n_load,volt,Vo ! apply voltage load to top electrode fini /solu antype,harm ! harmonic analysis harfrq,f1,f2 ! frequency range nsubs,10 ! number of substeps outres,all,all ! write all solution items to the result file kbc,1 ! stepped load solve fini /post1 /com,Calculate power dissipation at frequency = %f2%, Hz set,last ! read last data set etab,jh,jheat ! fill etable with Joule heat rates per unit volume etab,vol,volu ! fill etable with element volumes smult,dpower,jh,vol ! fill etable with element Joule heat rates ssum ! sum element Joule heat rates /com,Expected power dissipation = %P2d%, watt fini /post26 rfor,2,n_load,amps ! reaction current I prod,3,2,,,Y_ANSYS,,,1/Vo ! Y_ansys = I/V prod,4,1,,,,,,2*Pi*C ! 2*Pi*f*C cfact,tand,,,1 add,5,4,4,,Y_TARGET ! Y_target = 2*Pi*f*C*(tand+j) prcplx,1 prvar,Y_ANSYS,Y_TARGET fini /com, /com, *** Perform same frequency sweep using electrostatic elements /com, /PREP7 et,1,PLANE121,,,1 ! axisymmetric electrostatic element fini /solu antype,harm ! harmonic analysis harfrq,f1,f2 ! frequency range nsubs,10 ! number of substeps outres,all,all ! write all solution items to the result file kbc,1 ! stepped load solve fini /post1 /com,Calculate power dissipation at frequency = %f2%, Hz set,last ! read last dataset etab,jh,jheat ! fill etable with Joule heat rates per unit volume etab,vol,volu ! fill etable with element volumes smult,dpower,jh,vol ! fill etable with element Joule heat rates ssum ! summ up element Joule heat rates /com,Expected power dissipation = %P2d%, watt fini /post26 rfor,2,n_load,chrg ! reaction charge Q cfact,0,2*Pi prod,3,1,2,,Y_ANSYS,,,,1/Vo ! Y_ansys = j*2*Pi*Q/Vo prod,4,1,,,,,,2*Pi*C ! 2*Pi*f*C cfact,tand,,,1 add,5,4,4,,Y_TARGET ! Y_target = 2*Pi*f*C*(tand+j) prcplx,1 prvar,Y_ANSYS,Y_TARGET fini
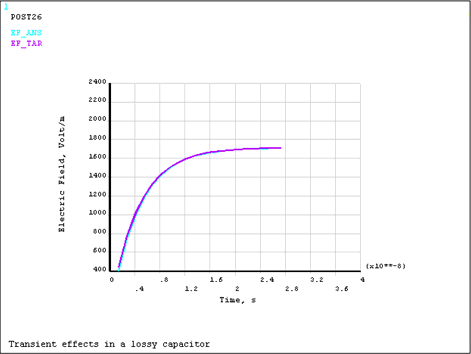
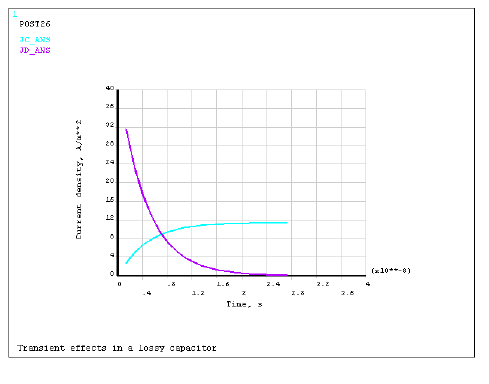
A parallel plate capacitor filled with a lossy dielectric, characterized by relative permittivity εr and resistivity ρ, is connected, in series with a resistor R, to a source of constant voltage U. The switch closes at time t = 0. Find the electric field and current density distributions in the capacitor as functions of time.
The capacitor and circuit parameters are:
| Length a = 3 cm |
| Width b = 1 cm |
| Thickness d = 0.5 cm |
| Permittivity (relative) = 12 |
| Resistivity = 150 Ωm |
| Resistance R = 1 kΩ |
| Voltage U = 12 volts |
The lossy capacitor is modeled with SOLID231 electric elements. Electrodes are defined by coupling VOLT degrees of freedom on the major surfaces of the capacitor. Lumped circuit components are modeled using CIRCU124 elements and they are connected to the capacitor via the master nodes. A transient analysis is performed to determine the electric field variation in the capacitor with time. Computed results for a selected element are compared in /POST26 to the values derived from the following analytical expression for the electric field:
E(t) = Es{1 - exp (-t/τ)}
where:
Es = steady-state electric field, Volts/m
S = capacitor plate area, m2
τ = time constant, seconds
and they are defined by:
S = ab
The following figures display the electric field and current density distributions as functions of time.
You can perform this example transient analysis using the Mechanical APDL commands shown below. Text prefaced by an exclamation point (!) is a comment.
Besides /POST26 commands to display the electric field and current density, this command listing includes the commands to print electric field, current density, electric flux density, and Joule heat rate. The current density and Joule heat rate output quantities are included to illustrate the coupling to magnetic and thermal analyses using companion magnetic and thermal elements, respectively.
/batch,list /title, Transient effects in a lossy capacitor /com, /com, Problem parameters: a=3.e-2 ! length, m b=1.e-2 ! width, m S=a*b ! area, m**2 d=0.5e-2 ! thickness, m epsr=12 ! relative permittivity of dielectric eps0=8.854e-12 ! free space permittivity, F/m rho=150 ! resistivity of dielectric, Ohm*m, R=1000 ! resistance, Ohm U=12 ! voltage, V Es=U/(S*R/rho+d) ! steady-state electric field, V/m tau=epsr*eps0*S*R/(S*R/rho+d) ! time constant, s /nopr /PREP7 emunit,epzro,eps0 ! Specify free-space permittivity ! Element attributes et,1,CIRCU124 ! Resistor et,2,CIRCU124,4 ! Voltage source et,3,SOLID231 ! 20-node brick electric solid r,1,R ! Real constants for circuit elements r,2,U mp,rsvx,1,rho ! Electric properties mp,perx,1,epsr ! Modeling and meshing type,3 mat,1 block,,d,,a,,b esize,d/2 vmesh,1 nsel,s,loc,x,0 cp,1,volt,all ! Couple nodes to model right electrode *get,n1,node,0,num,min ! Get master node on right electrode nsel,s,loc,x,d cp,2,volt,all ! Couple nodes to model left electrode *get,n2,node,0,num,min ! Get master node on left electrode nsel,all ! Circuit mesh *get,nmax,node,0,num,max n3=nmax+1 n4=n3+1 n,n3,a/2,-a n,n4,a/2,-a type,1 ! resistor real,1 e,n1,n3 type,2 ! voltage source real,2 e,n3,n2,n4 d,n2,volt,0 ! ground node fini /solu antype,transient ! transient analysis t1=6*tau time,t1 ! set analysis time deltim,t1/100 ! set time step outres,all,5 ! write results at every 5th substep ic,all,volt,0 ! initial conditions for VOLT solve fini ! Select nodes and elements for postprocessing n_post=node(d/2,a/2,b/2) nsel,s,node,,n_post esln,s *get,e_post,elem,0,num,min allsel /com, *** Results verification /post26 numvar,20 ! Electric field esol,2,e_post,,EF,x,EF_ANS exp,3,1,,,,,,-1/tau,-1 ! -exp(-t/tau) filldata,4,,,,1 ! 1 add,5,4,3,,EF_TAR,,,Es,Es ! E=Es*(1-exp(-t/tau)) ! Conduction current esol,6,e_post,,JC,x,JC_ANS prod,7,5,,,JC_TAR,,,1/rho ! Jc=E/rho ! Electric flux density esol,8,e_post,,NMISC,1,D_ANS prod,9,5,,,D_TAR,,,epsr*eps0 ! D=epsr*eps0*E ! Displacement and total (displacement+conduction) currents esol,10,e_post,,JS,x,JS_ANS add,11,10,6,,JD_ANS,,,,-1 ! Jd=Js-Jc deriv,12,9,1,,JD_TAR ! Jd=dD/dt add,13,7,12,,JS_TAR ! Joule heat generation rate per unit volume esol,14,e_post,,JHEAT,,HGEN_ANS prod,15,5,7,,HGEN_TAR! Jheat=E*Jc prvar,EF_ANS,EF_TAR,D_ANS,D_TAR prvar,JC_ANS,JC_TAR,JD_ANS,JD_TAR,JS_ANS,JS_TAR prvar,HGEN_ANS,HGEN_TAR /axlab,x, Time, s /axlab,y, Electric Field, Volt/m plvar,EF_ANS,EF_TAR ! Plot computed and expected EF /axlab,y, Current density, A/m**2 plvar,JC_ANS,JD_ANS,JS_ANS ! Plot computed currents fini /com, *** Coupling to thermal analysis /PREP7 et,1,0 et,2,0 et,3,90 ! companion thermal element esel,s,elem,,e_post ldread,hgen,,5,,,,rth ! read heat generation from the 5th substep bfelist,all,hgen ldread,hgen,,,,,,rth ! read heat generation from the last substep bfelist,all,hgen esel,all fini /com, *** Coupling to magnetic analysis /PREP7 et,3,236 ! companion magnetic element esel,s,elem,,e_post ldread,js,,5,,,,rth ! read current from the 5th substep bfelist,all,js ldread,js,,,,,,rth ! read current from the last substep bfelist,all,js esel,all fini
Another Ansys, Inc., publication, the Mechanical APDL Verification Manual, contains several examples of current conduction analysis: