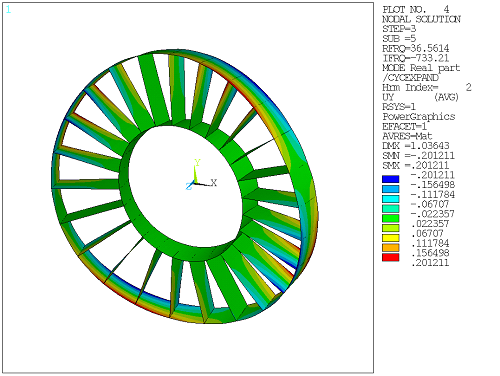
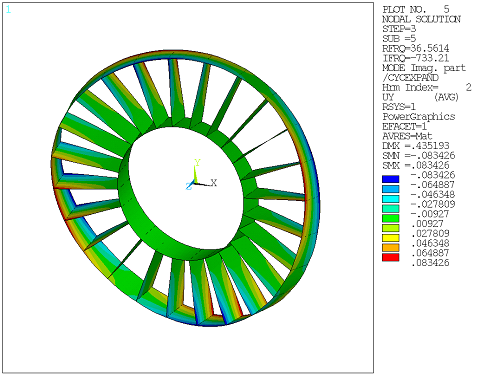
This example damped modal cyclic symmetry analysis presents a simplified ring-strut-ring structure used in many rotating-machinery applications.
This example is very similar to Example Modal Cyclic Symmetry Analysis, except that a damped modal analysis is performed. The component is a simplified fan inlet case for a military aircraft engine.
The problem specifications follow those of Example Modal Cyclic Symmetry Analysis, with the addition of alpha (mass proportional) and structural damping coefficients equal to 0.1.
! Damped Modal Cyclic Symmetry Analysis Example ! Ring-Strut-Ring Configuration ! Define constants r1=5 r2=10 d1=2 nsect=24 alpha_deg=360/nsect alpha_rad=2*acos(-1)/nsect ! Plot settings /view,1,1,1,2 /plopts,minm,0 /plopts,date,0 /plopts,logo,on /pnum,real,1 /number,1 ! Create a cyclic symmetry ring-strut-ring model /prep7 csys,1 k,1,0,0,0 k,2,0,0,d1 k,3,r1,0,0 k,4,r1,0,d1 l,3,4 arotat,1,,,,,,1,2,alpha_deg/2 k,7,r2,0,0 k,8,r2,0,d1 l,7,8 arotat,5,,,,,,1,2,alpha_deg/2 arotat,2,,,,,,1,2,alpha_deg/2 arotat,6,,,,,,1,2,alpha_deg/2 a,5,6,10,9 mshkey,1 et,1,181 r,1,0.20 r,2,0.1 mp,ex,1,10e6 mp,prxy,1,0.3 mp,dens,1,1e-4 esize,0.5 asel,,,,1,4 aatt,,1 asel,,,,5 aatt,,2 allsel cyclic amesh,all finish ! Perform a damped modal solve /solution antype,modal modopt,damp,6 ! Select damped eigensolver (unity norm by default) mxpand,6,,,yes alphad,0.1 ! Apply global alpha damping dmpstr,0.1 ! Apply structural damping dk,5,uz,0 solve finish /post1 set,list set,list,,, ,,, ,order /cycexpand rsys,1 ! Read results for "load step 1 - substep 3 - harmonic index 0" ! Plot the real and imaginary tangential displacement contour set,1,3,,real plns,u,y set,1,3,,imag plns,u,y ! Read results for "load step 13 - substep 1 - harmonic index 12" ! Plot the real tangential displacement contour set,13,1,,real plns,u,y ! Read results for "load step 3 - substep 5 - harmonic index 1" ! Plot the real and imaginary tangential displacement contour set,3,5,,real plns,u,y set,3,5,,imag plns,u,y
The following table describes the input listing and the steps involved in this example damped modal cyclic symmetry analysis in more detail.
| Step | Description | Command |
|---|---|---|
| 1. |
Start an interactive session. |
--- |
| 2. |
Create the Ring-Strut-Ring model. |
--- |
| 3. |
Specify a cyclic symmetry analysis and configure the database accordingly. | CYCLIC |
| 4. |
Mesh the areas. | AMESH,ALL |
| 5. |
Specify the damped eigensolver. | MODOPT,DAMP |
| 6. |
Apply global alpha damping. | ALPHAD,0.1 |
| 7. | Apply structural damping. | DMPSTR,0.1 |
| 8. |
Solve the modal cyclic symmetry analysis. | |
| 9. | List complex eigenvalues. | SET,LIST |
| 10. |
Specify the global cylindrical coordinate system. | |
| 11. |
Read results for "load step 1 - substep 3 - harmonic index 0." This can be done for both real and imaginary results. | |
| 12. |
Plot the real and imaginary tangential displacement contour. Executing this step causes the struts of the assembly to bend "in phase." | PLNSOL,U,Y |
| 13. | Read results for "load step 13 - substep 1 - harmonic index 12." | SET,13,1,REAL |
| 14. |
Plot the real tangential displacement contour. Executing this step causes the struts of the assembly to bend "out of phase." | PLNSOL,U,Y |
| 15. |
Read results for "load step 3 - substep 5 - harmonic index 1." | |
| 16. |
Plot the imaginary tangential displacement contour. ---- This step completes the example damped modal cyclic symmetry analysis. | PLNSOL,U,Y |
The results of your analysis should match those shown below.
Table 5.2: Sample Complex Eigenvalues
| SET | TIME/FREQ | LOAD STEP | SUBSTEP | CUMULATIVE | HRM-INDEX |
| 1 | -1.04E-04 | 1 | 1 | 1 | 0 |
| 2 | -5.40E-05 | 1 | 1 | 1 | 0 |
| 3 | -1.58E-02 | 1 | 2 | 2 | 0 |
| 4 | 5.40E-05 | 1 | 2 | 2 | 0 |
| 5 | -17.82 | 1 | 3 | 3 | 0 |
| 6 | 357.13 | 1 | 3 | 3 | 0 |
| 7 | 17.804 | 1 | 4 | 4 | 0 |
| 8 | -357.13 | 1 | 4 | 4 | 0 |
| 9 | -38.835 | 1 | 5 | 5 | 0 |
| 10 | 778.48 | 1 | 5 | 5 | 0 |
| 11 | 38.819 | 1 | 6 | 6 | 0 |
| 12 | -778.48 | 1 | 6 | 6 | 0 |
| 13 | -6.00E-12 | 2 | 1 | 7 | 1 |
| 14 | 7.57E-15 | 2 | 1 | 7 | 1 |
| 15 | -3.47E-05 | 2 | 2 | 8 | 1 |
| 16 | 3.87E-06 | 2 | 2 | 8 | 1 |
| 17 | -1.59E-02 | 2 | 3 | 9 | 1 |
| 18 | -3.87E-06 | 2 | 3 | 9 | 1 |
| 19 | -1.59E-02 | 2 | 4 | 10 | 1 |
| 20 | 1.63E-17 | 2 | 4 | 10 | 1 |
| 21 | -33.089 | 2 | 5 | 11 | 1 |
| 22 | 663.27 | 2 | 5 | 11 | 1 |
| 23 | 33.073 | 2 | 6 | 12 | 1 |
| 24 | -663.27 | 2 | 6 | 12 | 1 |
| 25 | 10.164 | 3 | 1 | 13 | 2 |
| 26 | -203.95 | 3 | 1 | 13 | 2 |
| 27 | 10.164 | 3 | 2 | 14 | 2 |
| ... | ... | ... | ... | ... | ... |
Note: Mode shape values may vary slightly depending on your computer system.