This section describes the solution controls and analysis settings for the modal and PSD analyses with the use of the residual vectors and modal expansion.
The modal analysis is performed using the Block Lanczos mode extraction method with the residual vector. (For additional information on the residual vector method, refer to Residual Vector Method in the Mechanical APDL Theory Reference and Residual Vector Method in Structural Analysis Guide)
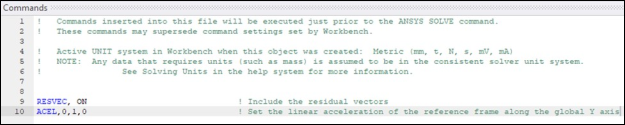
Linear acceleration loading is applied in the y direction (ACEL), as it is needed to generate the residual vector in conjunction with the downstream PSD analysis. Acceleration loading in the global y direction is chosen to generate the residual vector because in the subsequent PSD analysis, base excitation is applied in the same direction. Acceleration and Residual Vector are defined using the Command Snippet shown below since they are not supported in Workbench Mechanical.
For power spectral density (PSD) analysis, the base excitation is applied in the form of acceleration in the vertical y direction, which is represented in terms of the acceleration due to gravity. The PSD values for the input spectrum at different frequency points are given previously in Figure 20.8: PSD Base Excitation Values, and a damping ratio of 0.05 is selected.
In the modal superposition analysis, the dynamic response will be approximate if the applied loading excites the modes of a structure more than the modal analysis. The residual vector method is used to improve the accuracy of the dynamic response. The residual vectors are calculated using the static displacement response of the loads applied on the structure, which represent the linear combination of the truncated high frequency modes. The residual vectors are orthogonalized with respect to the eigenmodes extracted in the modal analysis to form orthogonalized residual vectors. The orthogonalized residual vectors are then used in modal superposition transient, harmonic, and spectral analyses to obtain more accurate modal based analyses results.
Because of the improved convergence properties of this method, fewer eigenmodes are required from the eigensolution. The dynamic response of the structure can be divided into two parts: contributions from the lower modes, and contributions due to the higher modes, which can be expressed as a combination of residual vectors.
The response power spectral density (RPSD) 1-σ displacement solutions are obtained with and without the residual vectors. The residual vectors are calculated in the modal analysis, and subsequently used in the PSD analysis with the same procedure. The residual vectors are used in a PSD analysis using a command snippet as shown below.
In the modal analysis, element results are written in the
Jobname.mode file prior to the expansion pass of the
subsequent mode-superposition (MSUPkey = YES on the
MXPAND command). In the Mechanical application, this is controlled
by the Store Modal Results property (in the
details view of Analysis Settings), which is set to
Program Controlled by default. For more details, see
Output Controls and
Analysis
Settings.
Results in Jobname.mode are written as a linear combination of the modal element results. Storing the modal element results significantly improves the efficiency in the downstream modal superposition expansion pass. Significant time is saved for the downstream modal transient, harmonic, and PSD analyses since the expansion pass does not need to execute element routines.
Full model modal analysis is carried out with and without storing the element results for the PSD analysis, and their efficiencies are compared. To run the analysis without storing the element results, set the Store Modal Results property to No.