This tutorial is divided into the following sections:
Inverse extrusion deals with the computation of the shape of a die that produces an extrudate of the desired shape. This tutorial illustrates how to handle a complex inverse extrusion problem. In this tutorial, slip conditions along the die walls are considered and evolution on the slip coefficient is enabled to aid convergence.
In this tutorial you will learn how to:
Define an evolution problem.
Create a sub-task to define an inverse extrusion problem.
Set material properties and boundary conditions for an inverse extrusion problem.
Specify multiple local remeshing regions.
This tutorial assumes that you are familiar with the menu structure in Polydata and Workbench and that you have solved or read 2.5D Axisymmetric Extrusion. Some steps in the set up procedure will not be shown explicitly.
This problem deals with the flow of a Newtonian fluid through a three-dimensional die. Due to the symmetry of the problem (the cross-section of the die is a polygon), the computational domain of the fluid is defined for a quarter of the geometry. Two planes of symmetry are defined.
The melt enters the die as shown in Figure 6.1: Problem Description at a flow rate 
= 10 cm3/s (a quarter of the actual flow rate) and the extrudate is obtained
at the exit.
The incompressibility and momentum equations are solved over the computational domain. The domain for the problem is divided into two sub-domains (as shown in Figure 6.1: Problem Description) so that specific remeshing algorithms can be applied in each sub-domain to accurately predict the die profile. Subdomain 1 represents the fluid as it enters and is confined by the die. Subdomain 2 corresponds to the extrudate that is in contact with the air (and can deform freely). The main aim of the calculation is to compute the geometry of the die to obtain the desired extrudate.
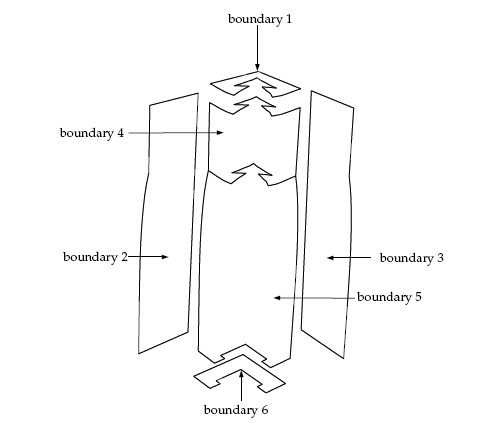
The boundary set for the problem are shown in Figure 6.2: Boundary Set for the Problem, and the conditions at the boundaries of the domains are given below
boundaries of the domains are:
boundary 1: flow inlet, volumetric flow rate
= 10 cm3/sboundary 2: symmetry plane
boundary 3: symmetry plane
boundary 4: slip conditions along the wall
boundary 5: free surface
boundary 6: flow exit
The following sections describe the setup and solution steps for this tutorial:
To prepare for running this tutorial:
Prepare a working folder for your simulation.
Download the
inverse_extrusion.zipfile here .Unzip the
inverse_extrusion.zipfile you have downloaded to your working folder.The mesh file
invext.mshcan be found in the unzipped folder.Start Workbench from .
Create a Fluid Flow (Polyflow Classic) analysis system by drag and drop in Workbench.
Save the Ansys Workbench project using File → , entering
inverse-extrusionas the name of the project.Import the mesh file (
invext.msh).Double-click the Setup cell to start Polydata.
When Polydata starts, the Create a new task menu item is highlighted, and the geometry for the problem is displayed in the Graphics Display window.
In the following steps you will define a new task representing the inverse extrusion model. Then, define a sub-task for the isothermal flow calculation.
Create a task for the model.
Create a new task
Select the following options:
F.E.M. task
Evolution problem(s)
Apply the evolution scheme on the slip coefficient along the outer wall of the die (boundary 4) when you define the slip boundary conditions.
Click Accept the current setup.
The Create a sub-task menu item is highlighted.
Create a sub-task for the isothermal flow.
Create a sub-task
Click Generalized Newtonian isothermal flow problem.
A dialog box appears asking for the title of the problem.
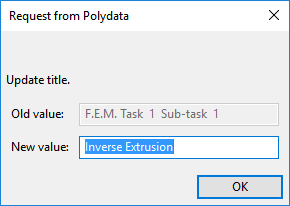
Enter
Inverse Extrusionas the New value and click .The Domain of the sub-task menu item is highlighted.
Define the domain where the sub-task applies.
This problem involves a free surface, so the domain is divided into two sub-domains; one for the region near the free surface (SUBDOMAIN_2) and the other for the rest of the domain (SUBDOMAIN_1). In this problem, the sub-task applies to both sub-domains, which is the default condition.
Domain of the sub-task
Accept the default selection of both subdomains by clicking Upper level menu.
The Material data menu item is highlighted.
Polydata indicates which material properties are relevant for your sub-task by graying out the irrelevant properties. In this case, viscosity, density, inertia terms, and gravity are available for specification. For this model you will only define the viscosity of the material.
Material Data
Click Shear-rate dependence of viscosity.
Click Power law.
The viscosity in this tutorial is given by the power law. For information on power law, see Power Law .
Specify the value of
, referred to as “fac”
in the graphical user interface (compare the equation at the top of
the Power law menu to the equation shown in the Power Law).
Modify fac
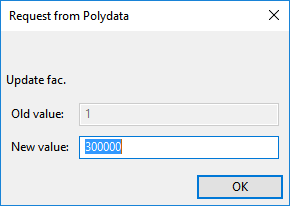
Enter
300000[units: poise] as the New value and click .Retain the default value for
, referred to as “tnat”
in the graphical user interface.
Modify tnat
Click to retain the default value of 1.
Specify the value for
, referred to as “expo”
in the graphical user interface.
Modify expo
Enter
0.75as the New value and click .Click Upper level menu three times to return to the Inverse Extrusion menu.
The Flow boundary conditions menu item is highlighted.
In the following steps you will set the conditions at each of the boundaries of the domain. When a boundary set is selected, its location is highlighted in red in the graphics window.
Flow boundary conditions
Set the conditions at the flow inlet (BOUNDARY_1).
Select Zero wall velocity (vn=vs=0) along BOUNDARY_1 and click .
Click Inflow.
Click Modify volumetric flow rate.
Polydata prompts you for the volumetric flow rate.
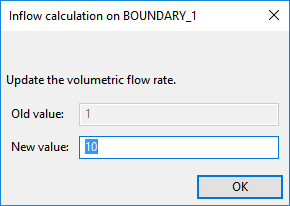
Enter
10[units: cm3/s] as the New value and click .Retain the default options of Automatic and Volumetric flow rate.
Click Upper level menu.
When the Automatic option is selected, Polydata chooses the most appropriate method to compute the inflow condition.
Set the conditions at the first symmetry plane (BOUNDARY_2).
In 2D axisymmetric problems, the axis of symmetry is automatically identified by Polydata, but for 3D flows, you must manually identify a plane of symmetry.
The normal velocity (
) and the tangential force (
) are set to zero on a symmetry plane. A
particle cannot cross the plane (
= 0) due to the symmetry, so the
particles flow at the same velocity on both sides of the symmetry
plane, leading to a zero tangential force.
Select Zero wall velocity (vn=vs=0) along BOUNDARY_2 and click .
Click Plane of symmetry (fs=0, vn=0).
Set the conditions at the second symmetry plane (BOUNDARY_3).
Select Zero wall velocity (vn=vs=0) along BOUNDARY_3 and click .
Click Plane of symmetry (fs=0, vn=0).
Set the conditions along the outer wall of the die (BOUNDARY_4).
Select Zero wall velocity (vn=vs=0) along BOUNDARY_4 and click .
Enable the evolution scheme on the slip coefficient.
The evolution scheme is used to aid with convergence by starting with a low value for the slip coefficient and slowly increasing the value of the coefficient to reach a no-slip condition. With a low value for the slip coefficient there is no swelling of the extrudate, simplifying the calculation. As the slip coefficient increases, the extrudate begins to swell because the fluid in contact with the wall slows down, which increases the velocity of the fluid in the center of the die. For more information on the evolution scheme, see Evolution Scheme.
Click EVOL at the top of the Polydata menu to enable the evolution inputs for the slip coefficient.
Click Slip conditions.
Click F(v) = Generalized Navier’s law.
For information on Navier’s law, see Appendix.
Specify the value of
.
Modify k
A dialog box appears asking you for the value of
.
Retain the default value of 1 for k and click .
Select the function f(S) = a*exp(b*S) + c + d*S.
You will retain the default values for a and b, and will modify the values for c and d.
Click Modify the value of c.
Hint: Scroll down to see Modify the value of c.
A dialog box appears asking for the new value of c.
Enter
0as the New value and click .Click Modify the value of d.
A dialog box appears asking for the new value of d.
Enter
0as the New value and click .Click EVOL at the top of the Polydata menu to disable the evolution inputs.
Click Upper level menu.
Retain the default value of 1 for e (
).Click Upper level menu two times to return to the Flow boundary conditions menu.
Set the conditions at the free surface (BOUNDARY_5).
In a steady-state problem, the velocity field must be tangential to a free surface, since no fluid particles go out of the domain through the free surface. This constraint is called the kinematic condition,
= 0. This equation requires an initial
condition (the starting line of the free surface). In this problem,
the starting line of the free surface is the intersection of boundary
4 and boundary 5 (see Figure 6.2: Boundary Set for the Problem).
Select Zero wall velocity (vn=vs=0) along BOUNDARY_5 and click .
Click Free surface.
Click Boundary conditions on the moving surface.
Select No condition along BOUNDARY_4 (the boundary where the free surface starts) and click .
Select Position imposed.
Click Upper level menu to return to the Boundary conditions on the moving surface menu.
Click Upper level menu at the top of the menu.
Click Outlet (Inv. prediction) to define the outlet of the moving surface.
In inverse extrusion problems, you have to predict the appropriate die exit cross-section to obtain a given extrudate cross-section. By defining the outlet of a free surface, inform Polyflow Classic the desired extrudate shape. Hence, you impose the outlet of the moving surface along the last section of the free jet as the outlet of the free surface. This section will not be modified during the calculation.
Select BOUNDARY_6 as the outlet of the moving surface and click .
Click Upper level menu to return to the Flow boundary conditions menu.
Set the conditions at the flow exit (BOUNDARY_6).
It is assumed that a uniform velocity profile is reached at the exit. The melt is not subjected to any externally applied stress at the exit, so the condition of zero normal and tangential forces is selected.
Select Zero wall velocity (vn=vs=0) along BOUNDARY_6 and click .
Click Normal and tangential forces imposed (fn, fs).
Accept the default value of 0 for the normal force,
, by clicking Upper level menu.Accept the default value of 0 for the tangential force,
, by clicking Upper level menu.
Click Upper level menu at the top of the Flow boundary conditions menu.
The Global remeshing menu item is highlighted.
The purpose of the remeshing technique is to relocate internal nodes according to the displacement of boundary nodes due to the motion of the free surface, since a part of the mesh is deformed. For information on remeshing technique, see Appendix.
Global remeshing
Specify the region where the remeshing is to be performed (SUBDOMAIN_2).
1–st local remeshing
Select SUBDOMAIN_1 and click .
SUBDOMAIN_1 is moved from the top list to the bottom list, indicating that only SUBDOMAIN_2 will be remeshed.
Click Upper level menu.
Define the parameters for the first local remeshing method.
For 3D extrusion problems where large deformations of the extrudate are expected, the optimesh remeshing technique is recommended. For information on optimesh remeshing technique see Appendix.
Optimesh-3D (extrusion
only)
Specify the initial plane for the optimesh remeshing technique, by selecting SUBDOMAIN_1 and clicking Modify.
Select Part of inlet section.
Select Upper level menu.
Specify the final plane for the remeshing technique, by selecting BOUNDARY_6 and clicking Modify.
Select Part of outlet section.
Select Upper level menu twice.
Polydata asks if you want to change from the surface kinematic condition to the line kinematic condition.
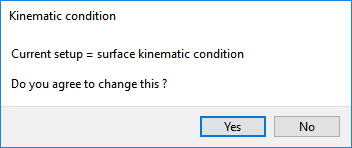
Click to use the line kinematic condition.
The line kinematic condition is recommended for extrusion problems, and must be used in combination with the optimesh remeshing technique.
Click Accept the current setup in the Element distortion check menu.
In complex extrusion simulations, the finite element mesh can undergo great deformations. The Element distortion check menu deals with the detection of all possible distortions of the elements. Accept default options.
Activate the inverse prediction.
Inverse prediction management
Click Enable the inverse prediction.
The technique of inverse prediction is selected to calculate the profile for the “constant section” region of the die.
Click Upper level menu.
Specify a second region for remeshing (SUBDOMAIN_1).
Click Creation of a local remeshing.
Select SUBDOMAIN_1 and click .
Click Upper level menu.
Click Constant section for prediction.
Specify the inlet plane of the system of planes, by selecting BOUNDARY_1 and clicking Modify.
Select Part of inlet section.
Select Upper level menu.
Specify the outlet plane for the system of planes, by selecting SUBDOMAIN_2 and clicking Modify.
Select Part of outlet section.
Select Upper level menu.
Click Upper level menu.
Click Accept the current setup.
Click Upper level menu two times.
The F.E.M. Task 1 menu is displayed.
All information relevant to iterative schemes (for the F.E.M. task calculations) can be modified in the Numerical parameters menu.
Numerical parameters
Specify the evolution parameters.
Modify the evolution parameters
Specify the final value of
.
Modify the upper limit
of S
Enter
20for the New value and click .Note: Setting the final value of
equal to 20 creates a large enough
slip coefficient that it is equivalent to a no-slip condition at the
die wall (BOUNDARY_4, as discussed in a previous step).Specify the initial value of
.
Modify the initial value of delta-S
Enter
2for the New value and click .Specify the minimum value of
.
Modify the min value of delta-S
Enter
0.1for the New value and click .Specify the maximum value of
.
Modify the max value of delta-S
Enter
3for the New value and click .Specify the maximum number of successful steps.
Modify the max number of successful
steps
Enter
30for the New value and click .
Click Upper level menu three times to return to the top-level Polydata menu.
After Polyflow Classic calculates a solution, it can save
the results in several different formats. Choose the one that is appropriate
for your postprocessor. In this case, save the outputs in IGES format, as well as the default format for CFD-Post.
Outputs
Retain the default output (CFD-Post) and click Enable Iges file output.
The default CFD-Post output is used for postprocessing with CFD-Post. The IGES output contains the modified geometry of the extrudate (after remeshing) calculated at every step of the evolution procedure. For information on IGES output, see Appendix.
Polydata asks you to confirm the current system units and fields that are to be saved to the results file for postprocessing.
Specify the system of units for the simulation.
Click Modify system of units.
Select Set to metric_cm/g/s/A+Celsius.
Click Upper level menu three times.
The top-level Polydata menu is displayed.
Save and exit
Click Accept current setup in the Convergence strategies menu.
Click Accept in the Field Management menu.
This confirms that the default Current field(s) are correct.
Click .
This accepts the default names for graphical output files (
cfx.res) that are to be saved for postprocessing, and for the Polyflow Classic format results file (res).
Run Polyflow Classic to calculate a solution for the model you just defined using Polydata.
Run Polyflow Classic by right-clicking the Solution cell of the simulation and selecting Update.
This executes Polyflow Classic using the data file as standard input, and writes information about the problem description, calculations, and convergence to a listing file (
polyflow.lst).A
cfx.resfile (corresponding to the eight evolution steps of the flow case) will be created.Check for convergence in the listing file.
Right-click the Solution cell and select Listing Viewer....
Workbench opens the View listing file dialog box, which displays the listing file.
It is a common practice to confirm that the solution proceeded as expected by looking for the following printed at the bottom of the listing file:
The computation succeeded.
Use CFD-Post to view the results of the Polyflow Classic simulation.
Double-click the Results tab in the Workbench analysis and read the results files saved by Polyflow Classic.
CFD-Post reads the solution fields that were saved to the results file.
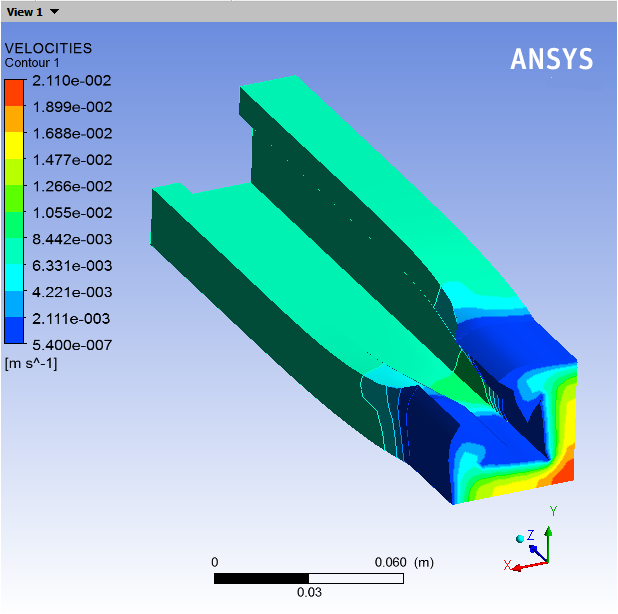
Display the velocity distribution on the boundaries.
Deselect Wireframe in the Outline tree tab, under User Locations and Plots.
Click the Insert menu and select Contour or click the
button.Click to accept the default name (Contour 1) and open the details view below the Outline tab.
Perform the following steps In the Geometry tab of the details view.
Click the
button next to Locations.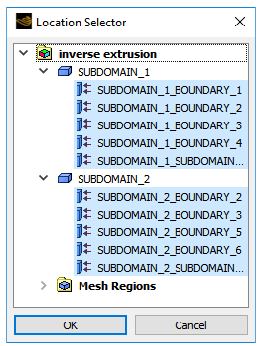
Select all topological entities under SUBDOMAIN_1 and SUBDOMAIN_2 in the Location Selector dialog box (use Shift for multiple selection) and click .
Select VELOCITIES from the Variable drop-down list (or by clicking
).Click .
You can see in Figure 6.3: Contours of Velocity Magnitude that the velocity is zero along the die wall, as expected, and there is a fully developed profile at the inlet of the die. At the die outlet, the velocity profile changes to become constant throughout the extrudate cross-section. The transition between these two states can be seen at the beginning of extrudate section.
Display contours of velocity in cross-sections.
Deselect the contours previously defined.
In the Outline tree tab, under User Locations and Plots deselect Contour 1.
Create the cross-section planes, at Z = 0, 3, 7 and 20 cm.
Select Plane from the Location drop-down menu (
). Click to accept the default name (Plane 1) and display the details view below the Outline tab.
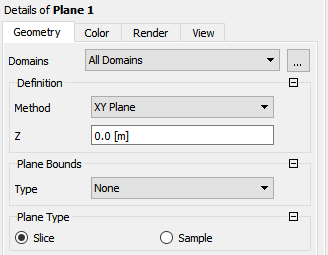
In the Geometry tab of the details view, select XY Plane from the Method drop-down list.
Enter
0for Z.Click .
Repeat steps 3.b.i.–v. to create the other planes at Z =
0.03,0.07, and0.1999m.In the Outline tree tab, under User Locations and Plots, deselect Plane 1, Plane 2, Plane 3, and Plane 4.
Click the Insert menu and select Contour or click the
button.Click to accept the default name (Contour 2) and open the details view below the Outline tree tab.
In the Outline tree tab under User Locations and Plots, select Wireframe.
Perform the following steps in the details view of Contour 2.
In the Geometry tab, click the
button next to Locations.
Select all planes under User Locations and Plots (use Shift for multiple selection).
Click .
Select VELOCITIES from the Variable drop-down list (or click
).In the Render tab, disable Lighting.
Click .
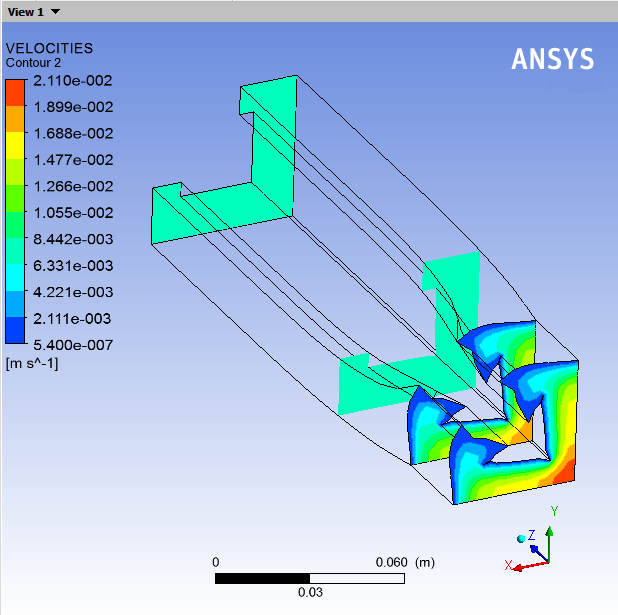
The velocity profiles planes are located at the flow inlet, the flow outlet, and planes just before and after the die exit as shown in Figure 6.4: Velocity Profile Planes.
Compare the velocity profile within the die to the velocity profile just after the die exit at the end of the computational domain.
The flow is fully developed in the die.
The velocity profile is flat in the extrudate, far away from the die exit. All particles in the cross-section plane are at the same velocity.
Just after the die exit, there is a transitional zone where the velocity profile is reorganized.
The velocity profile on the plane
= 7 cm is not fully
developed, but it is not flat either.
The velocity rearrangement is the source of the deformation of the extrudate.
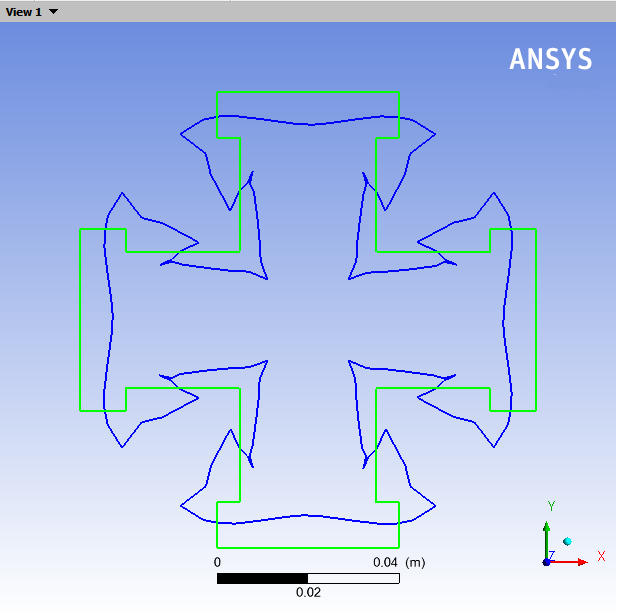
Compare the cross-section shape of the extrudate with die.
Simplify the display.
In the Outline tree tab, under User Locations and Plots, deselect Contour 2 and Wireframe.
Display the die shape using a polyline.
Select Polyline from the Location drop-down menu (
). Click to accept the default name (Polyline 1) and display the details view below the Outline tab.
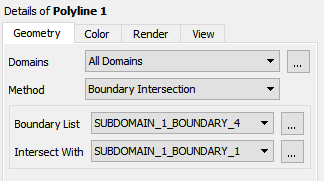
In the Geometry tab of the details view, select Boundary Intersection from the Method drop-down list.
Click
next to Boundary List and
select SUBDOMAIN_1_BOUNDARY_4. Click to close the Location Selector dialog box.Select SUBDOMAIN_1_BOUNDARY_1 from the Intersect With drop-down list.
In the Color tab, click
next to Color and select dark blue.Click .
Display the extrudate shape using a polyline.
Select Polyline from the Location drop-down menu (
). Click to accept the default name (Polyline 2) and display the details view below the Outline tab.
In the Geometry tab of the details view, select Boundary Intersection from the Method drop-down list.
Select SUBDOMAIN_2_BOUNDARY_5 from the Boundary List drop-down list.
Select SUBDOMAIN_2_BOUNDARY_6 from the Intersect With drop-down list.
Click .
Right-click in the graphic window and select View From +Z under Predefined Camera.
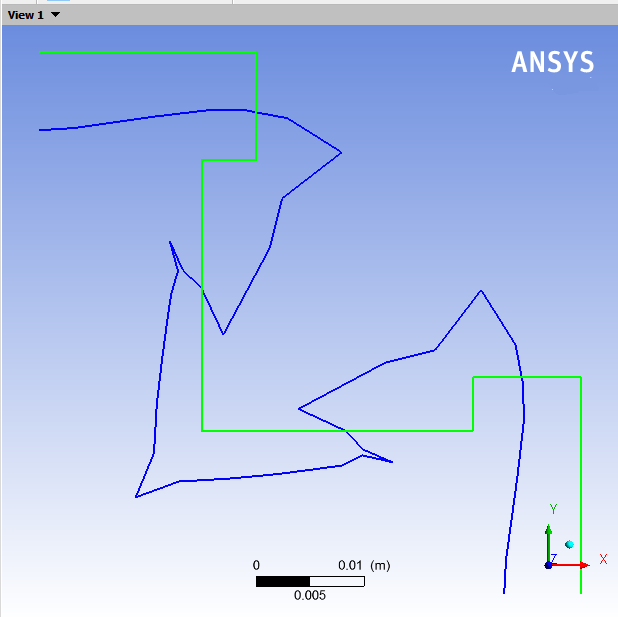
Restore the symmetry.
Click the Insert menu and select Instance Transform, or click the
button.Click to accept the default name (Instance Transform 1) and display the details view below the Outline tab.
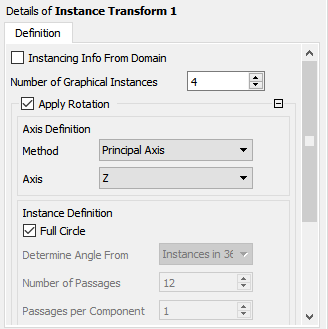
Perform the following steps in the Definition tab of the details view of Instance Transform 1:
Disable Instancing Info From Domain.
Enter
4for Number of Graphical Instances.Ensure Apply Rotation is selected.
Ensure Principal Axis and Z are selected for Method and Axis in the Axis Definition group box.
Enable Full Circle under Instance Definition.
Click .
In the Outline tree tab, under User Locations and Plots, right-click Polyline 1 and click (or double-click Polyline 1).
In the View tab of the details view, scroll down and enable Apply Instancing Transform.
Select Instance Transform 1 from the Transform drop-down list.
Click .
In the Outline tree tab, under User Locations and Plots, right-click Polyline 2 and click (or double-click Polyline 2).
Repeat steps 5..e–g.
You can use the central-mouse button to zoom in and out. This allows you to compare the size and shape of the flow inlet with that of the flow outlet without distortion due to perspective.
You can also click the fit view button (
) to properly center the image.
The deformation of the extrudate is the result of the rearrangement taking place at the die exit. Particles coming from high-speed regions in the die must slow down, while particles coming from low-speed regions must accelerate. You can change the speed by enlarging the flowing section. A tube of fluid at high speed in the die will enlarge its cross-section in the extrudate to decrease its average velocity. A tube of fluid at low speed in the die will reduce its cross-section in the extrudate in order to increase average speed. In Figure 6.5: Swelling of the Extrudate, you can see that the die design tool compensated for these effects. The central part of the cross-section where the fluid easily flowed in the original die has been reduced by the die design tool, while the extremities of the branches were enlarged because the flow was much slower in the original die. Since the combined effects of the cross-sectional enlargements and reductions are very difficult to guess, the numerical simulation is necessary to help the die designer reduce the number of trial-and-error iterations.
This tutorial introduced the concept of an inverse extrusion problem. You solved the problem assuming suitable conditions for the physics of the problem and Polyflow Classic predicted the shape of the die. You used multiple domain calculations with remeshing methods most suited to 3D inverse extrusion problems. The nonlinear problem was solved using an evolution technique to aid convergence.
The appendix contains the following sections:
The power law exhibits shear thinning (reduction in the viscosity with an increase in shear rate) that is a characteristic of many polymers. The viscosity in this tutorial is given by the power law:
 | (6–1) |
where:
= consistency factor
= power-law index
= natural time
is included in the equation to make the
units consistent.
The kinematic equation introduces nonlinear terms in the problem
that might lead to convergence difficulties. An evolution scheme is
available in Polyflow Classic to solve such highly nonlinear problems. Start
the calculation with a reduced value of the parameter(s) causing the
nonlinearity. Starting from the first solution, Polyflow Classic increments
the parameter(s) causing the nonlinearity and computes a second solution.
Starting from this new solution, Polyflow Classic increments the parameter(s)
again and computes a third solution. Following this procedure, Polyflow Classic increases
the value of each parameter up to its nominal value. In Polyflow Classic ,
this procedure is fully automated; the increments are automatically
adapted according to the results of previous calculations. Polyflow Classic uses
an evolution variable 
that is incremented during the evolution scheme.
S starts at an initial value of 
and is increased to a final value of 
. Each parameter l that you want to evolve is defined
as 
= 
.
Navier’s Law: The generalized Navier’s law is given by:
 | (6–2) |
where:
= tangential velocity of the fluid
= tangential velocity
of the wall
= material parameters
= material parameters
= 0 (assumed zero, by
default
Remeshing for the inverse extrusion problems is carried out in two stages. This model involves a free surface of unknown position. A portion of the mesh will be affected by the relocation of this boundary. Hence a remeshing technique that is suitable for 3D extrusion problems is applied to this part of the mesh. The free surface is entirely contained within subdomain 2, and hence only subdomain 2 will be affected by the relocation of the free surface.
This technique modifies the location of the section where the boundary conditions on the kinematic condition apply (the die-lip region). Apply local remeshing technique to the region between the entry section and the die-lip area (subdomain 1). In this tutorial, you define a "constant section" on this subdomain. This means that the die cross-section is constant from the die entry to the die exit (a parallel die). Using this two-stage remeshing technique, Polyflow Classic calculates the die profile that produces an extrudate of the desired shape. More complex deformations of the die are available via the definition of different local remeshings within the die.
The optimesh remeshing technique requires the direction of extrusion
to be parallel to the 
, 
, or 
axis, and all slices into which the remeshing domain
is cut must be perpendicular to the extrusion axis.
The domain to be remeshed is cut into a series of 2D slices (planes) in a direction perpendicular to the direction of extrusion, and each plane will be remeshed independently. For this process, Polyflow Classic requires the selection of the initial plane and the final plane. In this problem, the initial plane is the intersection of subdomain 2 with subdomain 1, and the final plane is the intersection of subdomain 2 with the flow exit (boundary 6).
An IGES output allows you to import the final geometry into a CAD program. This is useful when you are designing a die because you want to be able to manufacture the die predicted by the calculation. In the present case, you can compare the final shape of the predicted extrudate in an IGES format with the desired shape.