26.3. Modeling

Leveraging the symmetry of the structure, only half of the rubber boot is modeled. For the rubber boot, the hyperelastic material model is used. The shaft is considered as a rigid body.

Modeling for this problem involves the following tasks:

26.3.1. Model the Rubber Boot Seal

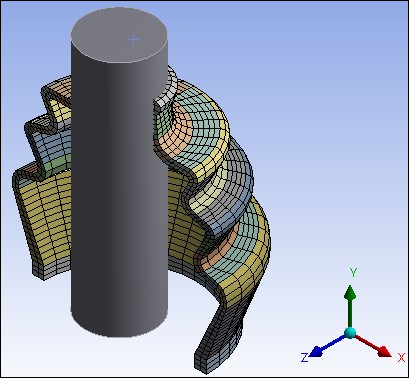
Lower order hexahedron elements (SOLID185) are used to mesh the rubber boot as shown in the figure below. This model has 3387 elements.

Figure 26.3: Linear Order Used for Mesh Elements

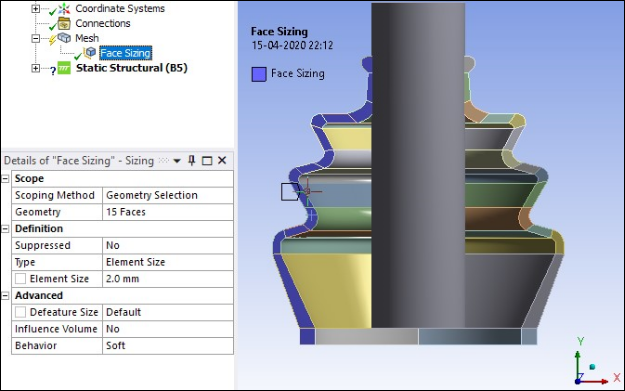
Face Sizing of 2 mm is used for 15 faces of the rubber boot as shown in the following figure.

Figure 26.4: Face Sizing Used for Mesh Elements

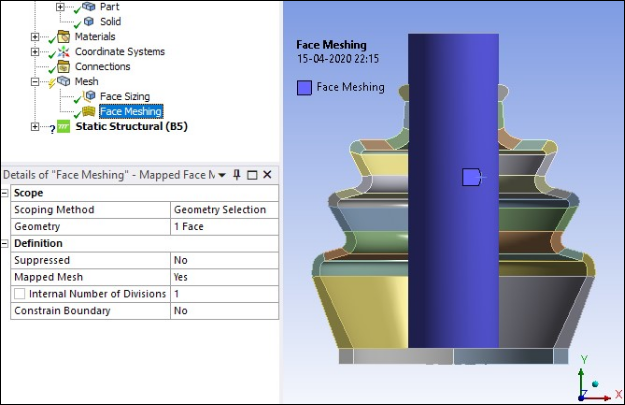
Mapped face meshing is used for the rigid shaft as shown in the following figure.

Figure 26.5: Mapped Face Meshing for Rigid Shaft

The final meshed model is shown in the figure below. It has total 2641 elements.

Figure 26.6: Meshed Model of the Assembly

26.3.2. Model the Contact Pairs

Three contact pairs are defined to simulate contact occurring in the rubber boot during the shaft movement:

Rigid flexible contact between the rigid cylindrical shaft and the inner surface of the rubber boot.
Self contact at the inner surface of the rubber boot using the surface-projection-based contact method.
Self contact at the outer surface of the rubber boot using the surface-projection-based contact method.

26.3.2.1. Rigid-flexible Contact Pair between Rigid Shaft and Rubber Boot

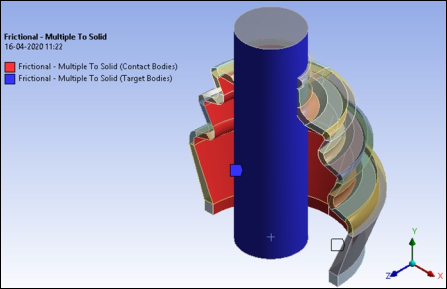
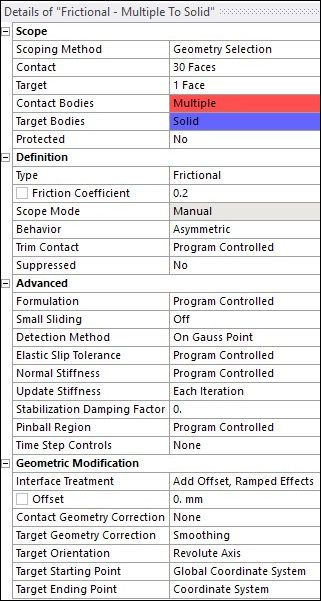
Frictional contact with a friction coefficient of 0.2 is defined between rigid shaft face and inner 30 faces of the rubber boot to be in contact.

Figure 26.7: Rigid-Flexible Contact Pair Between the Rigid Shaft and the Rubber Boot

The following contact settings are used.

Include interference with ramped effects (KEYOPT(9) = 2).
Set the location of the contact detection point at the gauss integration point (KEYOPT(4) = 0).
Update contact stiffness at each iteration (KEYOPT(10) = 2).

The following figure shows details of contact settings. The location of coordinate system used for target ending point is at the top face of shaft and has same orientation as global coordinate system.

Figure 26.8: Details of Rigid-Flexible Contact Pair between Rigid Shaft and Rubber Boot

26.3.2.2. Self Contact Pairs at Inner and Outer Surfaces of Rubber Boot

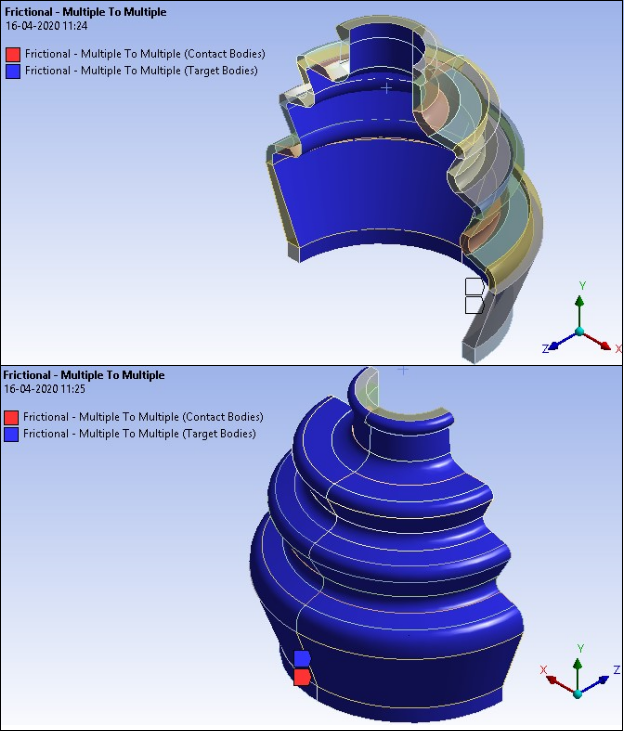
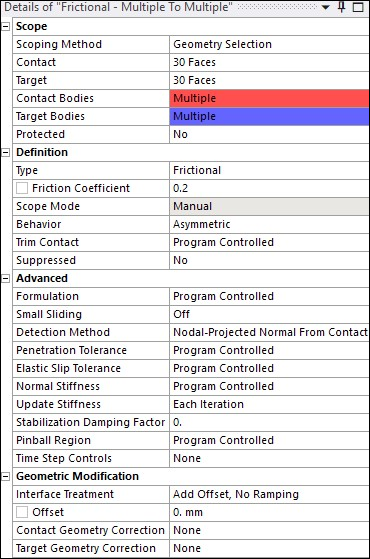
Two frictional self-contacts with a friction coefficient 0.2 are defined between the 30 inner and outer faces of rubber boot to be in self-contact.

Figure 26.9: Self Contact Pairs at Inner and Outer Surfaces of the Rubber Boot

To model a self contacting pair, both the target and contact surfaces are the same.

The following contact settings are used:

Surface-projection-based contact detection method (KEYOPT(4) = 3)
Update contact stiffness at each iteration (KEYOPT(10) = 2)

Figure 26.10: Detailed Settings for Self Contact Pairs on Inner and Outer Surfaces of Rubber Boot