VM-WB-MECH-024
VM-WB-MECH-024
Harmonic Response of a Single Degree of Freedom System
for Beams
Overview
| Reference: | Any basic Vibration Analysis book |
| Solver(s): | Ansys Mechanical |
| Analysis Type(s): | Harmonic Analysis |
| Element Type(s): | Beam |
Test Case
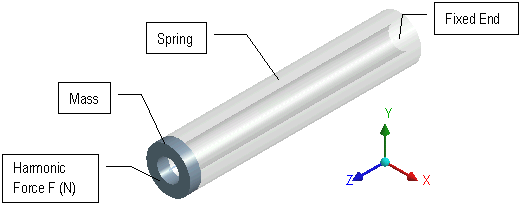
Two collinear beams form a spring-mass system. The density of the longer beam is kept very low so that it acts as a massless spring and the smaller beam acts as a mass. The end vertex of the longer beam (acting as a spring) is fixed. A Harmonic force F is applied on the free vertex of the shorter beam in z direction. Both beams have hollow circular cross-sections, as indicated below.
Scenario 1: Damping ratio = 0
Scenario 2: Damping ratio = 0.05
Find the z directional deformation of the vertex where force is applied at frequency F = 500 Hz for the above scenarios with solution intervals = 25 and a frequency range of 0 to 2000 Hz. Use both Mode Superposition and Full Method.
| Material Properties | |||
|---|---|---|---|
| Material | E (Pa) | ν | ρ (kg/m3) |
| Spring | 1.1e11 | 0.34 | 1e-8 |
| Mass | 2e11 | 0 | 7.85e5 |
| Geometric Properties | Loading | ||||||
|---|---|---|---|---|---|---|---|
|
|
Results Comparison
| Results | Target | Mechanical | Error (%) | |
|---|---|---|---|---|
| Mode-Superposition | Maximum z directional deformation without damping (m) | 4.11332 x 10-3 | 4.078 x 10-3 | -0.859 |
| Maximum z directional deformation with damping (m) | 4.11252 x 10-3 | 4.0765 x 10-3 | -0.876 | |
| Full Method | Maximum z directional deformation without damping (m) | 4.11332 x 10-3 | 4.1132 x 10-3 | -0.003 |
| Maximum z directional deformation with damping (m) | 4.11252 x 10-3 | 4.1022 x 10-3 | -0.251 | |