Droplet collision and coalescence are important physical phenomena in dense sprays. Droplets collide with each other, either due to fuel injection arrangement or droplets’ random motion induced by turbulence, affecting droplet property distributions locally and globally. Ansys Forte uses a phenomenological model to simulate the outcomes of droplet collisions. Knowing the properties of two colliding droplets, Forte determines the outcomes of collision from the following possibilities [58] , [65] :
Bounce Droplets do not contact due to a layer of gas between them.
Coalescence Droplets collide and form one larger droplet.
Near head-on separation Also known as "reflexive separation;" droplets separate after collision, possibly forming satellite droplets.
Off-center separation Also known as "grazing separation" or "stretching separation;" droplets separate after collision, possibly forming satellite droplets.
In general, the specific outcome depends on forces acting on the colliding pair of droplets. At low Weber numbers, surface forces dominate over liquid inertia forces, and the droplets are more likely to coalesce. At higher Weber numbers, the liquid inertia forces become more important, and separation after collision is more likely to occur. With further increase of the Weber number, the dominant liquid inertia forces cause shattering of the colliding droplets as they separate, forming a group of small droplets.
More specifically, prediction of collision outcomes is governed mainly by three non-dimensional numbers:
Droplet size ratio:
in which
and
are the diameters of the smaller and larger droplets, respectively;
Droplet Weber number:
in which ρ is the liquid density, U is the magnitude of relative velocity between droplets, and σ is the surface tension coefficient.
Impact parameter: B. The impact parameter defines the geometric orientation of the interacting droplets. More detailed descriptions can be found in [58] and [42] .
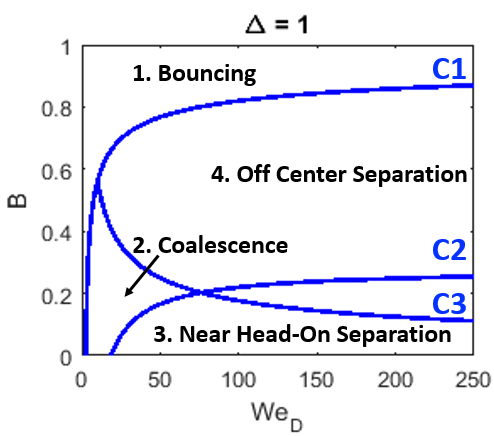
The distribution of collision outcomes in the impact parameter and Weber number space is visualized in Figure 6.8: Typical regime map for determining the collision outcome [58] , assuming that the droplet size ratio is one:
The three curves (C1, C2, and C3) that distinguish collision outcome regimes are summarized in Table 6.1: Definitions of the three curves presented in Figure 6.8: Typical regime map for determining the collision outcome [58] .
Table 6.1: Definitions of the three curves presented in Figure 6.8: Typical regime map for determining the collision outcome [58]
In which Θ' is a shape factor of value 3.351, ,
, and
are functions of Δ and
. Detailed definitions can be found in Ref. [58]
.
In the separation outcomes (outcomes 3 and 4), there is a possibility of satellite droplets being produced. Munnannur’s model [58] predicts the sizes and numbers of these secondary droplets also.
To simulate droplet collision in sprays, it is practical to employ a stochastic and sampling approach similar to that in [5] . Instead of computing the collision process for every droplet, Ansys Forte treats droplets in a parcel as a whole when assessing their probability of colliding with droplets in another parcel. All the droplets in parcel A are assumed to behave in the same way, they either do or do not collide with the droplets in parcel B based on the probability.
The probable number of collisions of the two colliding droplet parcels can be written as:
(6–73) |
in which and
are the numbers of droplets within the two parcels,
and
are the droplets radii,
is the magnitude of relative velocity between droplets,
is the time step, and
is the control volume in which the parcels are allowed to collide.
As in Amsden’s approach [5] , the probability that the two parcels will collide or not is computed based on the probable number of collisions (n ̅). The probability is compared to a random number chosen in the interval (0,1) to decide whether the collision will happen or not.
Droplets are more likely to collide with those in close neighborhood. However, the definition of close neighborhood is challenging, considering its validity in physics and the associated numerical issues. In the collision model of O’Rourke, [65] spray particles are allowed to collide only if they reside in the same computational cell. In a cylindrical mesh, the cell size around the spray axis can be very small, preventing collisions from occurring. This treatment introduces dependency of spray collision results on the CFD mesh size, which is not desirable. Ansys Forte implements three advanced models to remove the dependency of numerical parameters such as mesh size.