The lift force, FL, is a force transversal to the direction of the relative velocity between particle and fluid velocities. This force is generated by a series of factors, the most common are fluid velocity gradients or a rotating particle that generates different pressure values at the sides of the particle. In most cases, the lift force is insignificant compared to the drag force, so there is no reason to include this extra term. If the lift force is significant (for example, if the phases separate quickly), it may be appropriate to include this term.
The lift force is usually calculated based on the lift coefficient , and uses a cross product between the relative velocity and the curl of the
velocity, which naturally provides the force direction, as can be seen in the following
equation:
(3–67) |
where is the actual lift force,
is the particle volume,
is the relative velocity between fluid and particle and
is the density of the fluid.
The value of the lift coefficient, , is generally calculated from correlations derived from experimental data or
analytical/numerical solutions. The available laws for the calculation of the lift force
coefficient in Rocky are detailed in the following sections.
In all lift force laws supported by Rocky DEM-CFD coupling, the common factors in the
definition of the correlations are the usual Reynolds number based on the relative velocity
between the particle and fluid ) as given by equation Equation 3–6 , and the vorticity Reynolds number
given by:
(3–68) |
as well as the particle's rotational Reynolds number defined as:
(3–69) |
where is the particle angular velocity vector.
It is common to consider the ratio of and
, and it is usually expressed in terms of a variable
, defined as:
(3–70) |
The Saffman lift force [25], [24] is due to a pressure difference developed on a particle in a fluid velocity gradient. The higher velocity at one side of the particle develops a lower pressure and the lower velocity on the other side develops a higher pressure (according to the Bernoullis principle). Saffman analyzed the lift force for low (relative) Reynolds numbers and reached the following expression for the force in a one-dimensional configuration:
(3–71) |
This expression can be generalized for three-dimensional flows as:
(3–72) |
Moreover, using the definition of the and
, the Saffman lift coefficient can be written as:
(3–73) |
It can be noted that if the relative velocity is positive, there is a lift force
toward the higher velocity of the continuous phase, whereas if the relative velocity is
negative, the lift force is oriented toward the lower continuous phase velocity. The
expression for the lift coefficient in Equation 3–73 is valid
for .
Mei [23] expanded the validity of the Saffman law to higher relative Reynolds number values, by defining a correction term acting over the Saffman lift coefficient in the following way:
(3–74) |
where the correction term is given by:
(3–75) |
With this correction, the correlation is still limited only to spherical particles,
but is valid for wider ranges:,
.
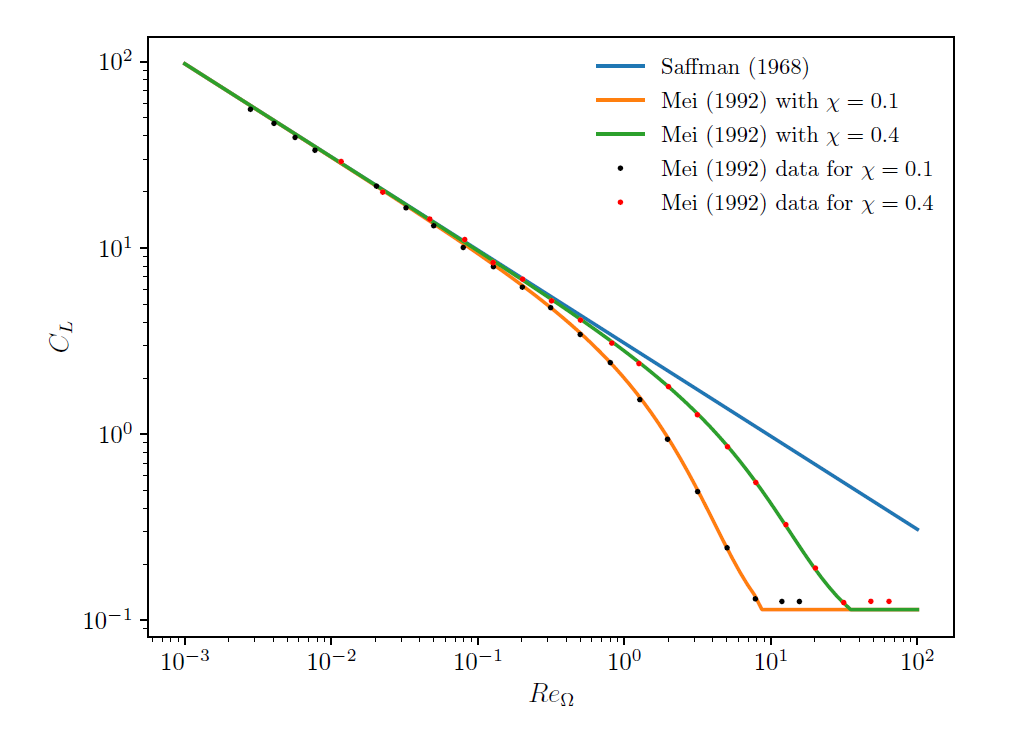
Figure 3.8: Comparison of Saffman and
Mei lift laws. compares the shear lift coefficients
, given by equations Equation 3–73 and Equation 3–75, with the numerical results of Dandy and Dwyer [22] used by Mei [23] to evaluate the Saffman law
for
and
. As
increases, it was found experimentally that the lift coefficient
decreases and it levels off around
. Satisfactory agreement can be observed in the Saffman law for both
as long as
. The Mei law is observed to agree with the experimental data over a
wider range of
.