In Ansys Chemkin, the reactor cluster capability has been extended to optionally perform reactor-to-reactor and global balancing of heat in the reactor network model. We assume that heat exchange is a combination of convection/conduction and/or radiation. These extensions allow prediction of the net heat release from the reactor-network system. for example, in modeling a fuel-cell reforming system, one reactor can represent a combustor and the combustor can serve as the heat source for activating the catalytic reactions in another reactor that represents the reformer. Heat balance is a critical issue in the design of many catalytic devices.

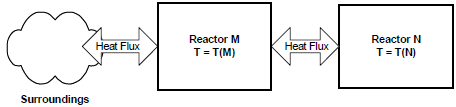
Figure 8.3: Schematic of the thermal communication of a reactor in a network shows a schematic of a reactor unit or module and the heat flow that may occur into or out of that module in a general reactor network. An individual reactor (for example, Reactor M in Figure 8.3: Schematic of the thermal communication of a reactor in a network ) may be thermally connected to one or more other modules and to the system's external environment. A general heat balance for Reactor M must account for conduction, convection, and radiation heat exchange. Transient simulations must also account for heat capacity effects.

Figure 8.3: Schematic of the thermal communication of a reactor in a network

If heat transfer is allowed between Reactor M and Reactor N, (see Figure 8.3: Schematic of the thermal communication of a reactor in a network ), the transient energy balance equation for Reactor M becomes:

(8–34)

where is the heat flow coming from Reactor N to Reactor M and is given as:

(8–35)

The first term of Equation 8–35 describes the heat flow caused by localized heat transfer modes such as conduction and convection and the second term is an optically-thin model for thermal radiation heat transfer between the two reactors. The area, , is the "external" surface area that is available for heat transfer, which may be different from the internal surface area available for surface chemistry. Since and , the properties of a "heat exchange matrix" can be obtained from Equation 8–35 , with the additional relationships:

(8–36)

and

(8–37)

In this way, the total energy among the reactors is conserved in the absence of any external heat loss. The user input parameters that control this reactor-to-reactor heat transfer are described in the Chemkin Input Manual (QXCO and QXRA keywords).