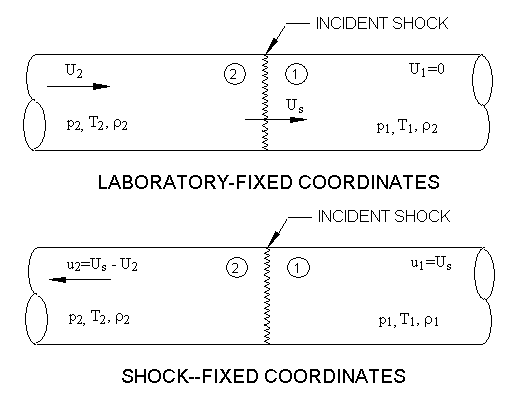
In relating the pressures, temperatures and densities immediately across
the shock, it is conventional to consider the gas motion in relation to the
shock front. In such a frame of reference, the gas
enters the shock at a relative velocity , and leaves with a relative velocity
. In shock tube jargon, the shock is
then considered to be at rest;
is the gas velocity measured in shock-fixed coordinates and
is that measured in laboratory-fixed coordinates. These two frames of
reference are related by:
(7–5) |
(7–6) |
where is the shock velocity. Gas conditions associated with the incident shock
in the two coordinate systems are shown in Figure 7.3: Laboratory-fixed and Incident-shock-fixed coordinate systems
. The
Rankine-Hugoniot relations for properties across the
incident shock front are
(7–7) |
(7–8) |
(7–9) |
Utilizing the equation of state (Ideal Gas Law) and Equation 7–7
to eliminate the velocity
and
from Equation 7–8
and Equation 7–9
results in the following
expressions for the pressure and temperature ratios across the incident shock:
(7–10) |
(7–11) |
Since we assume no change in gas composition across the shock,
is a function of temperature alone and, hence, Equation 7–10
and Equation 7–11
represent a system of two
equations in two unknowns. The solution gives
and
when conditions before the incident shock are specified. Knowing these,
is determined from the equation of state and
from Equation 7–7
.
An iterative procedure is employed to solve Equation 7–10
and Equation 7–11
for and
. Letting
and
be the temperature and pressure ratios, respectively, across the shock,
Equation 7–10
can be solved for
in terms of
(see Equation 7–13
) to yield
(7–12) |
This expression is then substituted into Equation 7–11
to yield one equation with one
unknown, . Within Ansys Chemkin, a routine called
ZEROIN [52], which finds the zeros of functions, is employed to determine the value of
that satisfies this equation. An initial guess for
is provided by assuming that the test
gas is ideal (
and
are constant and independent of temperature). For ideal gases
(7–13) |
where is the specific heat ratio and
is the Mach
number of the incident shock.
(7–14) |
Many times the experimentalist reports the incident shock speed,
, and temperature and pressure behind the shock,
and
, respectively. Before the experiment can be modeled, however, the gas
velocity behind the shock must be determined. Employing the equation of state in Equation 7–10
to eliminate
results in
(7–15) |
This equation and Equation 7–11
again represent two equations
in two unknowns. The solution gives and
and from these the density in region 1 is determined from the equation of
state. The velocity behind the shock,
, is determined from Equation 7–7
. The solution to Equation 7–15
and Equation 7–11
is analogous to that already
described for Equation 7–10
and Equation 7–11
.