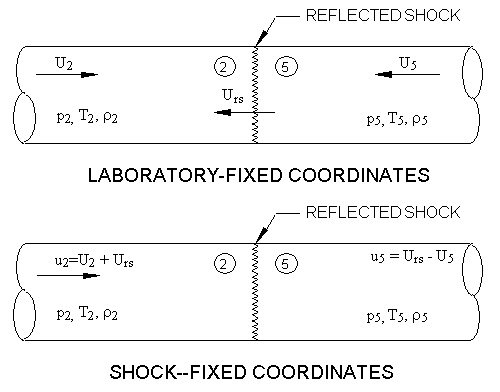
For reflected shocks, shock-fixed and laboratory-fixed coordinates are
again employed, but now shock-fixed coordinates refer to the reflected shock, which moves at
velocity . Considering the reflected shock to be at rest, gas at condition 2 flows
into the shock front and gas at condition 5 flows out.
The velocities in the two coordinate systems are related by:
(7–16) |
and
(7–17) |
The gas velocity measured in shock-fixed coordinates with respect to the
reflected shock is . Gas conditions associated with the reflected shock in the two coordinate
systems are shown in Figure 7.4: Laboratory-fixed and reflected-shock-fixed coordinate systems
.
The Rankine-Hugoniot relations for properties across the reflected shock are
(7–18) |
(7–19) |
and
(7–20) |
By analogy with Equation 7–7
, Equation 7–8
and Equation 7–9
, the solution to the above set
of coupled equations is found by finding the values of and
which satisfy
(7–21) |
and
(7–22) |
where
(7–23) |
When the gas is assumed to be at rest behind the reflected shock (that is,
), then the reflected
shock velocity,
, is given by
(7–24) |
Only in the ideal case is the gas behind the reflected shock at rest,
however. Non-idealities cause the gas to move in the same direction as the incident shock
and, hence, at conditions different from those calculated assuming . Therefore, often the velocity of the reflected shock, as well as that of
the incident shock, is measured. Then the values of
and
are computed so as to satisfy the
Rankine-Hugoniot relationships using these measured velocities. Having determined
and
, the density of the gas at condition 5 can be determined from the equation
of state and
, from Equation 7–18
.
Initial estimates for and
can be obtained by again assuming ideal gas behavior. The temperature
ratio across the incident shock when
and
are constant is given by Equation 7–13
and the pressure ratio
by
(7–25) |
Letting and
be defined as the following density ratios:
(7–26) |
(7–27) |
then the equation of state, Equation 7–13 and Equation 7–21 to Equation 7–25 can be combined to show that for temperature-independent specific heats
(7–28) |
(7–29) |
(7–30) |
(7–31) |
and
(7–32) |
Even in the event that is specified, and hence
is not necessarily zero, we still assume that the gas is at rest when
solving the conservation
equations. Only the initial state of the gas is
modified by the non-ideal reflected
shock velocity. Because of this, for reflected shock
problems, we find it more convenient to use laboratory-time as the independent variable,
since then the boundary-layer effects are of no
consequence. For such cases, laboratory-time and gas-particle time are the same.